inch2m <- 2.54/100
pound2kg <- 0.45
data_diabetes <- diabetes %>%
mutate(height = height * inch2m, height = round(height, 2)) %>%
mutate(waist = waist * inch2m) %>%
mutate(weight = weight * pound2kg, weight = round(weight, 2)) %>%
mutate(BMI = weight / height^2, BMI = round(BMI, 2)) %>%
mutate(obese= cut(BMI, breaks = c(0, 29.9, 100), labels = c("No", "Yes"))) %>%
mutate(diabetic = ifelse(glyhb > 7, "Yes", "No"), diabetic = factor(diabetic, levels = c("No", "Yes"))) %>%
na.omit()Exercises (introduction to linear models)
Exercise 1 (Fitting linear model) Going back to the diabetes data, fit linear regression models using vector-matrix notations to model BMI based on age [years] and waist [m] measurements. In particular, define design matrix \(\mathbf{X}\), vector of observations \(\mathbf{Y}\) and vector of parameters \(\boldsymbol\beta\) and use \[\hat{\mathbf{\beta}}= (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\] to find beta values estimates.
Check your calculations by fitting the model using lm() function.
The below code can get you started.
Exercise 2 (Hypothesis testing) Your colleague Anna is interested in association between BMI and cholesterol, both total cholesterol (chol) and high density lipoprotein fraction (hdl). She has correctly fitted linear model using lm() function but her computer broke and she only has the below output:
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 3.471e+01 2.940e+00 11.808 < 2e-16 ***
# chol 1.965e-05 1.231e-02
# hdl -9.371e-02 3.220e-02Can you help Anna finding out whether chol and hdl are significantly associated with BMI? What are the t-value statistics and the corresponding p-values? Calculate these values without fitting the model and then fit the model to double check your calculations.
Exercise 3 (Evaluate model fit) After helping Anna you got interested in whether your initial model containing age and waist is a better fit to the data than Anna’s model containing chol and hdl. Evaluate model fit by calculating \(R^2(adj)\) based on the equation:
\[R^2(adj) = 1-\frac{\frac{RSS}{n-p-1}}{\frac{TSS}{n-1}}\] where
- \(p\) is the number of independent predictors, i.e. the number of variables in the model, excluding the constant and \(n\) is the number of observations.
Check your calculations using lm() function.
Hint: If reg holds a fitted linear regression model, you can assess the estimated BMI values by accessing reg$fitted.values and residuals via reg$residuals.
Solution. Exercise 1
inch2m <- 2.54/100
pound2kg <- 0.45
data_diabetes <- diabetes %>%
mutate(height = height * inch2m, height = round(height, 2)) %>%
mutate(waist = waist * inch2m) %>%
mutate(weight = weight * pound2kg, weight = round(weight, 2)) %>%
mutate(BMI = weight / height^2, BMI = round(BMI, 2)) %>%
mutate(obese= cut(BMI, breaks = c(0, 29.9, 100), labels = c("No", "Yes"))) %>%
mutate(diabetic = ifelse(glyhb > 7, "Yes", "No"), diabetic = factor(diabetic, levels = c("No", "Yes"))) %>%
na.omit()
# define Y
Y <- data_diabetes %>% select("BMI") %>% as.matrix()
# define X
X <- cbind(rep(1, nrow(data_diabetes)), data_diabetes$age, data_diabetes$waist)
X <- as.matrix(X)
# alternatively we case use model.matrix() to define X
X <- model.matrix(~ age + waist, data = data_diabetes)
# least square estimate
beta.hat <- solve(t(X)%*%X)%*%t(X)%*%Y
print(beta.hat)
## BMI
## (Intercept) -2.39192911
## age -0.05716479
## waist 35.46856117
# check calculations using lm() function
reg_1 <- lm(BMI ~ age + waist, data = data_diabetes)
summary(reg_1)
##
## Call:
## lm(formula = BMI ~ age + waist, data = data_diabetes)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.6952 -2.8803 -0.5864 2.2229 18.7443
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.39193 2.95646 -0.809 0.4200
## age -0.05716 0.02551 -2.241 0.0267 *
## waist 35.46856 2.68192 13.225 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.358 on 127 degrees of freedom
## Multiple R-squared: 0.5841, Adjusted R-squared: 0.5776
## F-statistic: 89.19 on 2 and 127 DF, p-value: < 2.2e-16Solution. Exercise 2
Under the null hypothesis \(H_0: \beta = 0\) 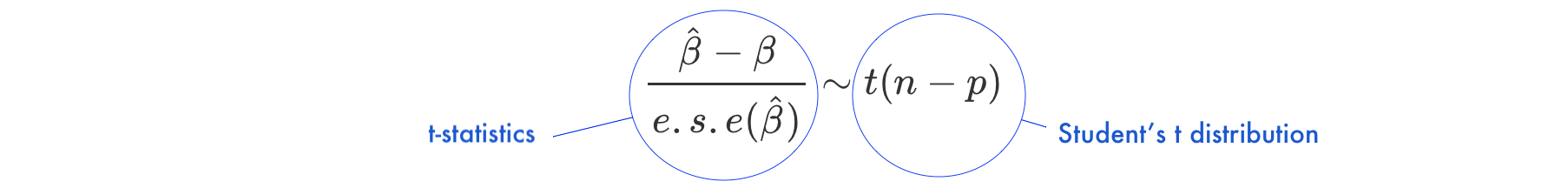
- \(n\) is number of observations
- \(p\) is number of model parameters
- \(\frac{\hat{\beta}-\beta}{e.s.e(\hat{\beta})}\) is the ratio of the departure of the estimated value of a parameter, \(\hat\beta\), from its hypothesized value, \(\beta\), to its standard error, called
t-statistics - the
t-statisticsfollows Student’s t distribution with \(n-p\) degrees of freedom
This means that to check if the there is an association between chol and BMI we check if there is enough evidence to reject the null hypothesis of \(H_0: \beta = 0\). Here, t-statistics equals to \(\frac{\hat{\beta}-\beta}{e.s.e(\hat{\beta})} = \frac{1.965\times 10^{05} - 0}{1.231\times 10^{05}} = 0.001596263\) and a corresponding p-values can be found:
2*pt(0.001596263, df=130 - 3, lower.tail = F)
## [1] 0.9987289Assuming 5% significance level, we do not have enough evidence to reject the null hypothesis in favor of the alternative as p-value is large \(p = 0.99873 > 0.05\). This means we do not observe association between chol and BMI.
Analogously, for age we have t-statistics equal to \(\frac{\hat{\beta}-\beta}{e.s.e(\hat{\beta})} = \frac{-9.371\times 10^{02} - 0}{3.220\times 10^{02}} = -2.910248\) and a corresponding p-value equals to:
2*pt(-2.910248, df=130 - 3, lower.tail = T)
## [1] 0.004265831Here, p-value is small and we can thus reject the null hypothesis in favour of the alternative and conclude that there is an association between hdl and BMI.
To check our calculations we can re-fit the linear model and print the entire summary.
reg_2 <- lm(BMI ~ chol + hdl, data = data_diabetes)
summary(reg_2)
##
## Call:
## lm(formula = BMI ~ chol + hdl, data = data_diabetes)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.8952 -4.8988 -0.9225 3.0629 21.7951
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.471e+01 2.940e+00 11.808 < 2e-16 ***
## chol 1.965e-05 1.231e-02 0.002 0.99873
## hdl -9.371e-02 3.220e-02 -2.910 0.00426 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.538 on 127 degrees of freedom
## Multiple R-squared: 0.0643, Adjusted R-squared: 0.04956
## F-statistic: 4.363 on 2 and 127 DF, p-value: 0.0147Solution. Exercise 3
n <- nrow(data_diabetes)
p <- 2 # beta for age and beta for waist (model 1)
p <- 2 # beta for chol and beta for hdl (model 2)
# calculate TSS
TSS <- sum((data_diabetes$BMI - mean(data_diabetes$BMI))^2)
# calculate RSS and R2_adj (model 1)
# model BMI ~ age + waist
reg_1 <- lm(BMI ~ age + waist, data = data_diabetes)
reg <- reg_1
RSS <- sum((reg$residuals)^2)
R2_adj <- 1 - (RSS/(n-p-1))/(TSS/(n-1))
print(R2_adj)
## [1] 0.5775851
# calculate RSS and R2_adj (model 2)
# model BMI ~ chol + hdl
reg_2 <- lm(BMI ~ chol + hdl, data = data_diabetes)
reg <- reg_2
RSS <- sum((reg$residuals)^2)
R2_adj <- 1 - (RSS/(n-p-1))/(TSS/(n-1))
print(R2_adj)
## [1] 0.04956166# check calculations
summary(reg_1)
##
## Call:
## lm(formula = BMI ~ age + waist, data = data_diabetes)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.6952 -2.8803 -0.5864 2.2229 18.7443
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.39193 2.95646 -0.809 0.4200
## age -0.05716 0.02551 -2.241 0.0267 *
## waist 35.46856 2.68192 13.225 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.358 on 127 degrees of freedom
## Multiple R-squared: 0.5841, Adjusted R-squared: 0.5776
## F-statistic: 89.19 on 2 and 127 DF, p-value: < 2.2e-16
summary(reg_2)
##
## Call:
## lm(formula = BMI ~ chol + hdl, data = data_diabetes)
##
## Residuals:
## Min 1Q Median 3Q Max
## -12.8952 -4.8988 -0.9225 3.0629 21.7951
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.471e+01 2.940e+00 11.808 < 2e-16 ***
## chol 1.965e-05 1.231e-02 0.002 0.99873
## hdl -9.371e-02 3.220e-02 -2.910 0.00426 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.538 on 127 degrees of freedom
## Multiple R-squared: 0.0643, Adjusted R-squared: 0.04956
## F-statistic: 4.363 on 2 and 127 DF, p-value: 0.0147–>