PCA and Gene Expression

Workshop on Advanced Data Visualization

Author

Lokesh Mano

Published

05-May-2025

1 PCA

Let us first make a PCA object. For this, we will use the VST data, because it makes sense to use the normalized data for building the PCA. To run PCA, we use the R function prcomp(). It takes in a matrix where samples are rows and variables are columns. Therefore, we transpose our count matrix using the function t(). If we do not transpose, then PCA is run on the genes rather than the samples.

Note

In this section, we will talk about PCA and how to plot a PCA object using ggplot. But the idea of plottig the results of any multi-dimwntionality reduction methods like MDS/PCoA, NMDS, tSNE, UMAP and many others would in theory be the same as PCA.

gc_vst <- read.table("../../data/counts_vst.txt", header = T, row.names = 1, sep = "\t")
vst_pca <- prcomp(t(gc_vst))

After you computer the PCA, if you type the object vst_pca$ and press TAB, you will notice that this R object has multiple vecors and data.frames within it. Some of the important ones are

  • sdev: the standard deviations of the principal components
  • x: the coordinates of the samples (observations) on the principal components.
  • rotation: the matrix of variable loadings (columns are eigenvectors).
Note

There are quite a few functions in R from different packages that can run PCA. So, one should look into the structure of the PCA object and import it into ggplot accordingly!

1.1 Variance of components (Scree plot)

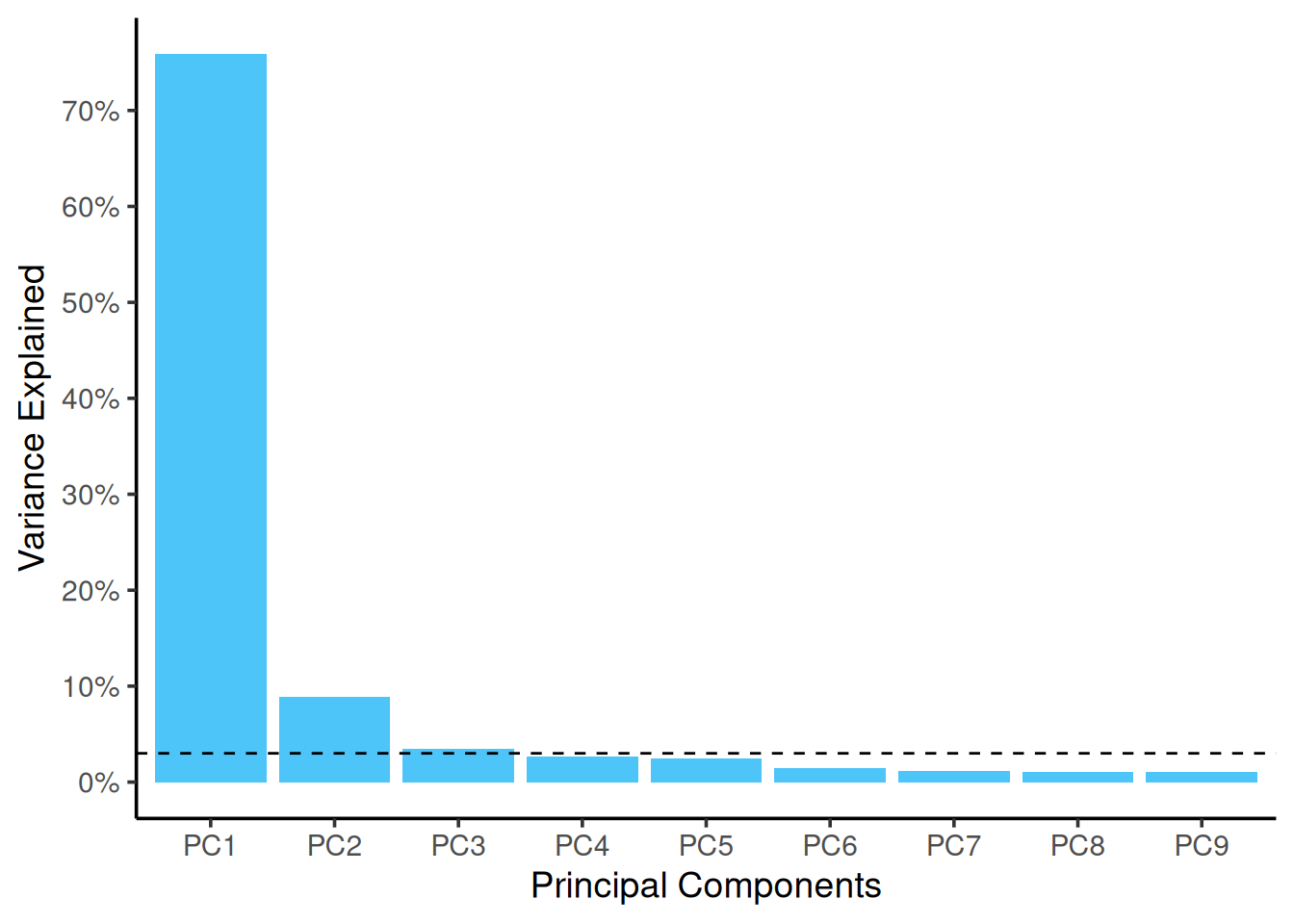
First, let us look into plotting the variance explained by the top PCs.

frac_var <- function(x) x^2/sum(x^2)
library(scales)

vst_pca$sdev %>% 
  as_tibble() %>% 
  frac_var() %>% 
  mutate(Comp = colnames(vst_pca$x)) %>% 
  slice(1:9) %>% 
  ggplot(aes(x=Comp, y = value)) + 
  geom_bar(stat = "identity", fill = "#4DC5F9") +
  geom_hline(yintercept = 0.03, linetype=2) +
  xlab("Principal Components") +
  scale_y_continuous(name = "Variance Explained", breaks = seq(0,0.8,0.1), labels = percent_format(accuracy = 5L)) +
  theme_classic(base_size = 14)

1.2 PCA plot

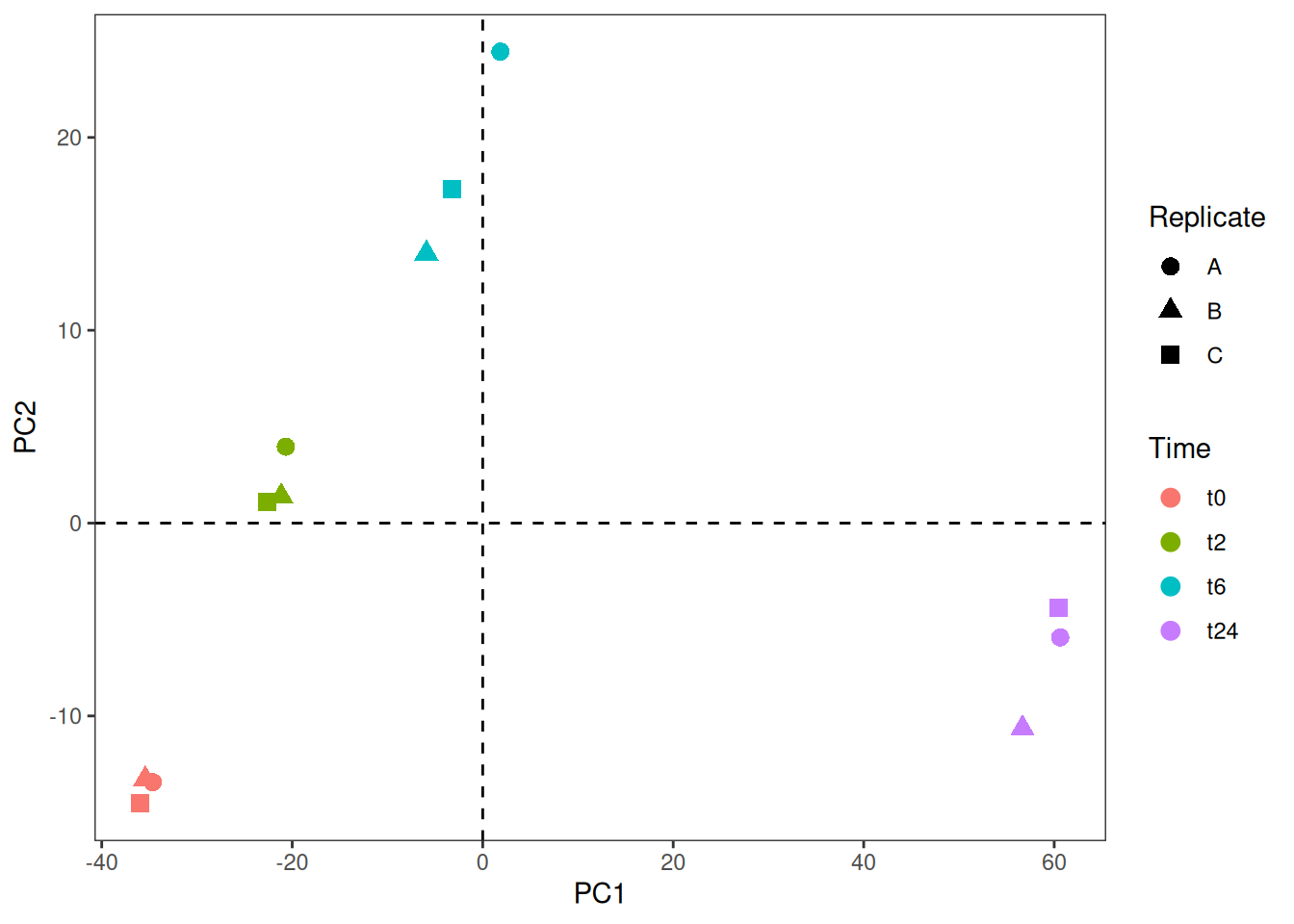
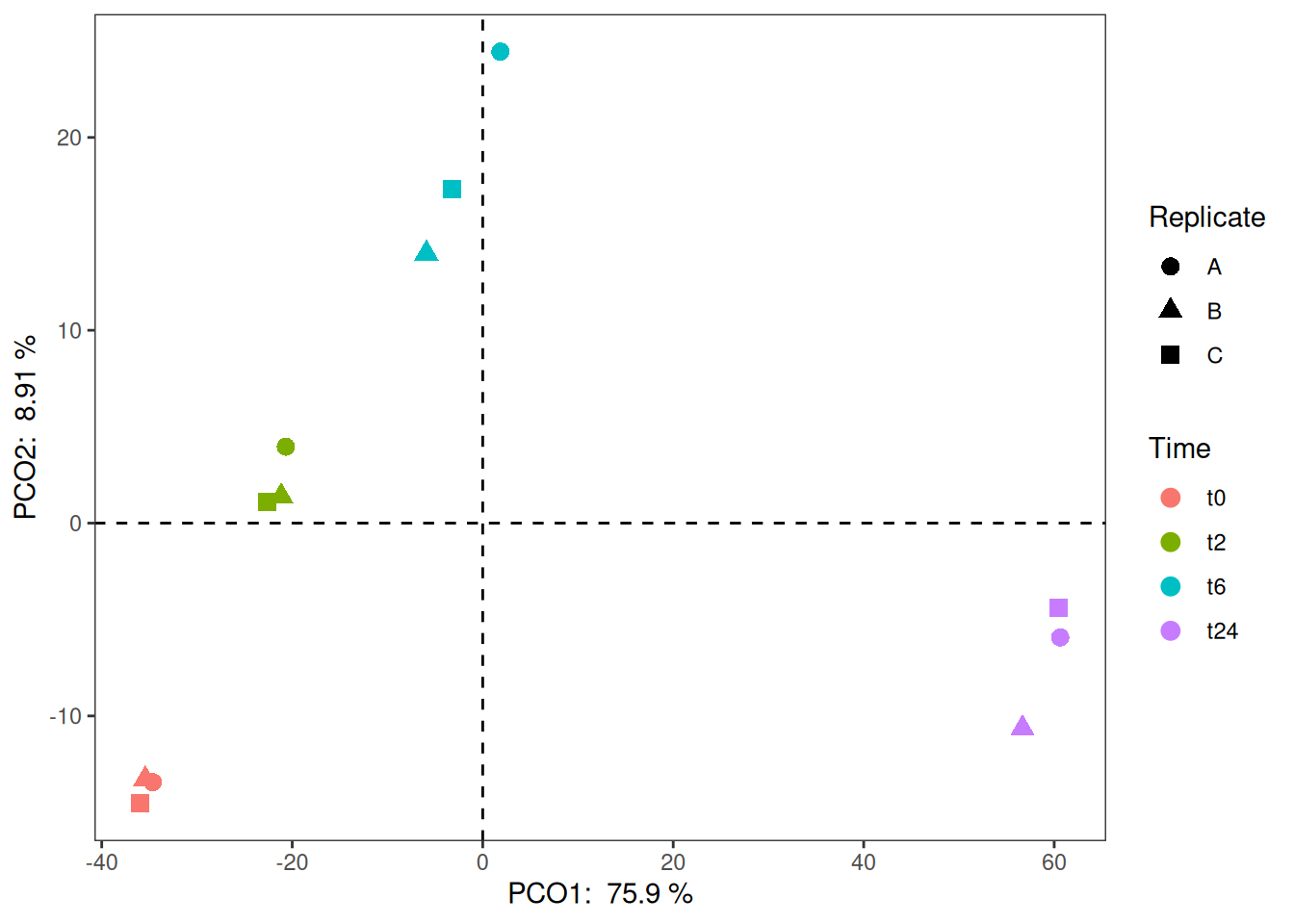
So, looks like the first two components explain almost 85% of the data. Now, let us look into building a plot out of these components. From the above object, to get the scatter plot for the samples, we need to look into vst_pca$x. Then, we combine this data (as shown below) with the metadata to use different aesthetics and colors on the plot.

vst_pca$x
                 PC1        PC2        PC3         PC4        PC5         PC6
Sample_1  -34.641623 -13.435531   6.486032   0.2742477   6.406502   5.6703279
Sample_2  -35.431333 -13.277983   5.171377   0.3540945   3.953216   6.9974341
Sample_3  -35.938795 -14.544994   2.885351  11.3414829  -5.950082 -10.8497916
Sample_4  -20.672358   3.962013  -1.414301 -10.4819194   0.195882  -2.8003847
Sample_5  -21.155503   1.390981  -6.644132  -7.4002617  -6.505502   0.9771040
Sample_6  -22.662075   1.115504  -9.801356  -6.3107519  -7.431833   0.6592987
Sample_7    1.862762  24.449057  12.865650   4.4029501  -5.822040   4.1873901
Sample_8   -5.909698  13.992629 -14.775686  10.9789567   8.967097   2.2612207
Sample_9   -3.233544  17.321871   5.196746  -2.5142966   6.983077  -7.2580550
Sample_10  60.630406  -5.930071   6.993097  -5.7393184   4.254238  -2.6905179
Sample_11  56.669696 -10.638879  -5.860598  -0.4646609   5.216763  -1.3748865
Sample_12  60.482067  -4.404596  -1.102179   5.5594769 -10.267317   4.2208603
                 PC7        PC8        PC9       PC10       PC11         PC12
Sample_1  -7.6896364 -7.5508580  1.1936551  0.2382806  0.7901002 4.899206e-14
Sample_2   5.8962070  9.0662471  1.0449651 -0.2284545 -1.3982703 5.084128e-14
Sample_3   1.4353811 -0.7461021 -1.4769949 -0.2114041  0.5247079 4.830164e-14
Sample_4   1.2992058 -2.3863551 -6.1089574  0.1510797 -9.1851796 4.973973e-14
Sample_5  -2.7487548  2.7353990 -4.5686381  6.6024251  6.9911571 4.892961e-14
Sample_6   2.1391551 -2.3567136  7.7925047 -6.9400619  1.3499685 5.057196e-14
Sample_7   5.2166866 -4.0805978 -0.2292610  1.4574679  1.2200771 5.066433e-14
Sample_8  -0.1684735  0.1448735 -3.9822133 -2.5610601  0.5182664 4.997044e-14
Sample_9  -5.4663572  5.2056738  6.4295279  1.6062665 -0.5133496 4.986636e-14
Sample_10  0.8277618  0.5767198 -4.9156730 -6.8596253  4.8748004 4.900247e-14
Sample_11  5.8886122 -3.9566331  4.4374522  6.9835771 -0.4457707 4.726081e-14
Sample_12 -6.6297877  3.3483466  0.3836326 -0.2384911 -4.7265074 5.044576e-14

And, if you check the class() of this object, you will realize that this is a matrix. To be able to comfortably use tidyverse on this object, we must first convert this to a data.frame.

vst_pca_all <- vst_pca$x %>%
  as.data.frame() %>%
  rownames_to_column(var = "Sample_ID") %>%
  full_join(md, by = "Sample_ID")

# Just to keep the order the right way.
vst_pca_all$Sample_Name <- factor(vst_pca_all$Sample_Name, levels = c("t0_A","t0_B","t0_C","t2_A","t2_B","t2_C","t6_A","t6_B","t6_C","t24_A","t24_B","t24_C"))
vst_pca_all$Time <- factor(vst_pca_all$Time, levels = c("t0","t2","t6","t24"))
vst_pca_all$Replicate <- factor(vst_pca_all$Replicate, levels = c("A","B","C"))

ggplot(vst_pca_all, aes(x=PC1, y=PC2, color = Time)) +
  geom_point(size = 3, aes(shape = Replicate)) +
  geom_vline(xintercept = 0, linetype=2) +
  geom_hline(yintercept = 0, linetype=2) +
  theme_bw() +
  theme(panel.grid.major = element_blank(), 
        panel.grid.minor = element_blank())

1.3 Loading plot

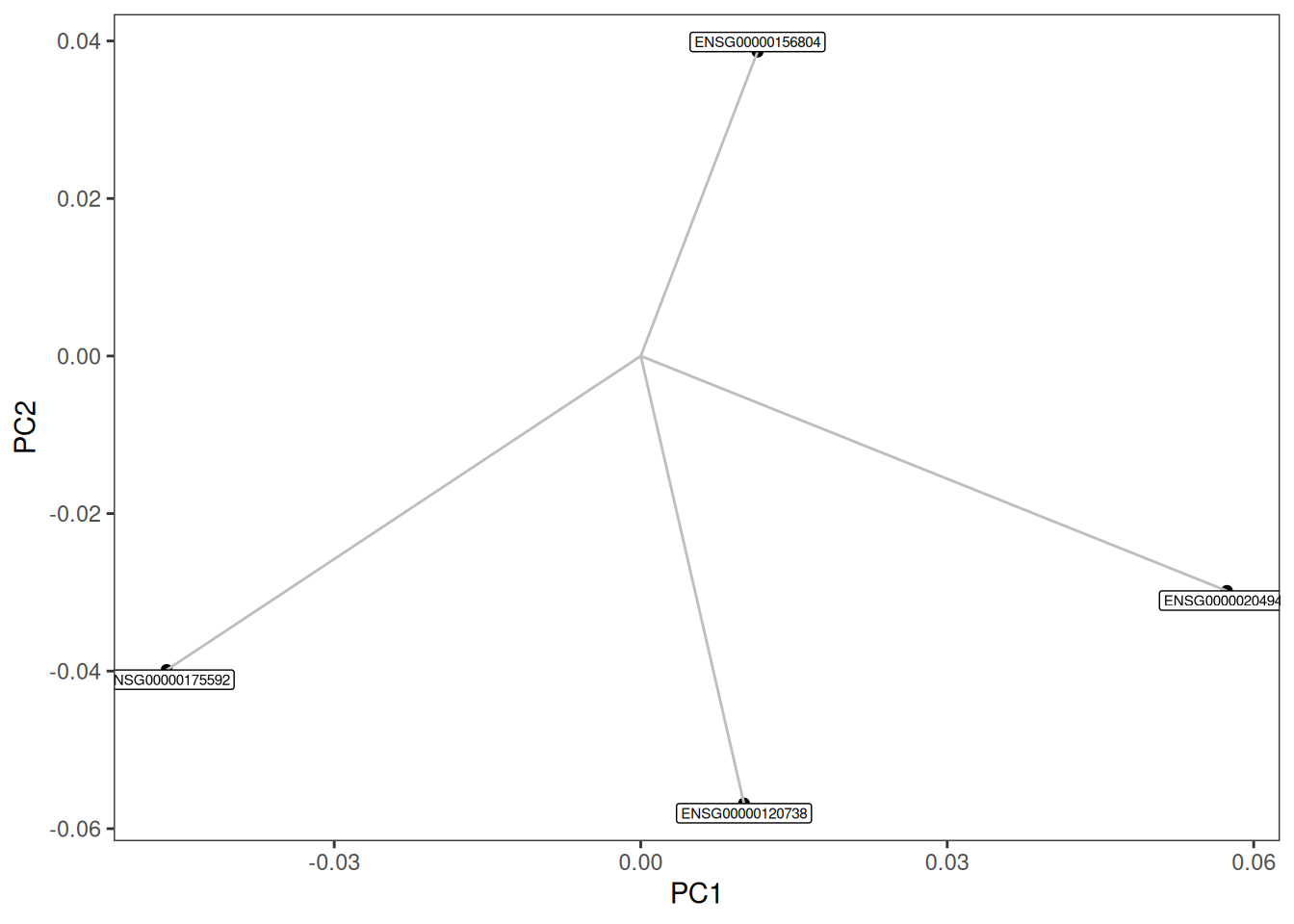
Now, let us say you want to plot the four genes that contribute the most to the four directions in the PCA plot. We could obtain them by looking at the vst_pca$rotation matrix. We could get those genes and their respective coordinates as follows.

genes.selected=vst_pca$rotation[c(which.max(vst_pca$rotation[,"PC1"]), which.min(vst_pca$rotation[,"PC1"]), which.max(vst_pca$rotation[,"PC2"]), which.min(vst_pca$rotation[,"PC2"])),c("PC1","PC2")]
genes.selected <- genes.selected %>%
  as.data.frame() %>%
  rownames_to_column(var = "Gene_ID")
genes.selected

A loading plot shows how strongly each variable (gene) influences a principal component. As an example, we could plot the four genes we selected.

ggplot(genes.selected, aes(x=PC1, y=PC2)) +
  geom_point() +
  geom_segment(aes(xend=PC1, yend=PC2), x=0, y=0, color="Grey") +
  geom_label(aes(x=PC1, y=PC2, label=Gene_ID), size=2, vjust="outward") +
  theme_bw() +
  theme(panel.grid.major = element_blank(),  panel.grid.minor = element_blank())

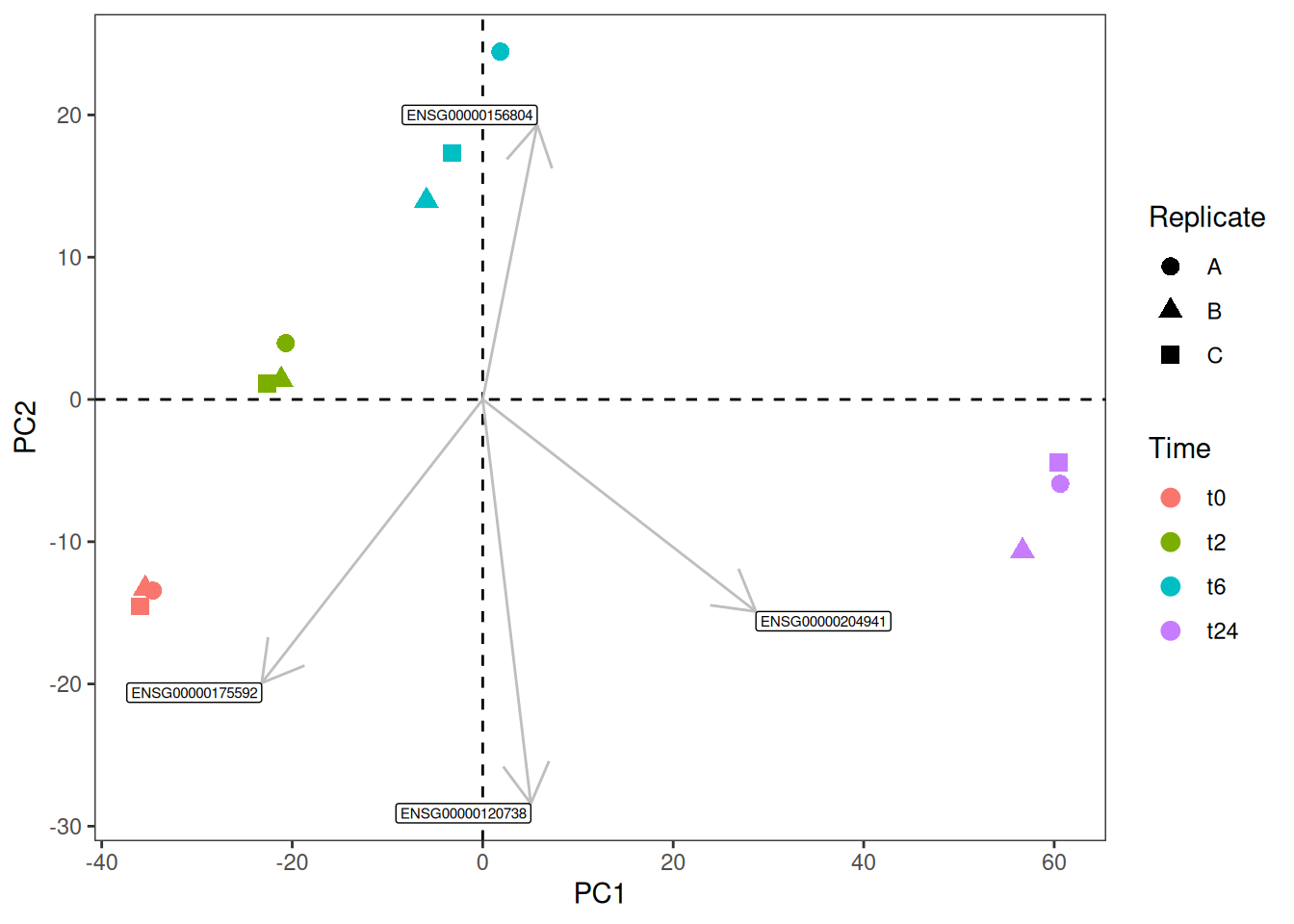
1.4 PCA bi-plot

By merging the PCA plot with the loadings plot one can create a so-called PCA bi-plot.

scale=500
ggplot(data=vst_pca_all, mapping=aes(x=PC1, y=PC2)) +
     geom_point(size = 3, aes(shape = Replicate, color = Time)) +
     geom_vline(xintercept = 0, linetype=2) +
     geom_hline(yintercept = 0, linetype=2) +
     geom_segment(data=genes.selected, mapping=aes(xend=scale*PC1,yend=scale*PC2), x=0, y=0, arrow=arrow(), color="grey") +
     geom_label(data=genes.selected, mapping=aes(x=scale*PC1,y=scale*PC2, label=Gene_ID), size=2, hjust="outward", vjust="outward") +
     theme_bw() +
     theme(panel.grid.major = element_blank(),  panel.grid.minor = element_blank())

Note

Similarly, let us say, you have environmental variables (continous variables like pH and so on) from the same samples and you would like to see how they would fit this bi-plot. One can use envfit() function from the vegan package, this function would return both the p-value and the coordinates of each of the variables in your environmental matrix. Then you could subset the significant variables and plot them in the same way as above.

2 Exercise I

Now, as I have mentioned earlier, building a plot similar to PCA really depends on how the object looks like. Now, let us try to make a MDS or PCoA plot from the same data as we have used. Here is how you get the MDS object in R.

gc_dist <- dist(t(gc_vst))
gc_mds <- cmdscale(gc_dist,eig=TRUE, k=2)
Task 1.1

Now, try to replicate the example MDS plot below if you have enough time.

Tip

The mds object gc_mds has “eigenvalues”. You can calculate the variance by Variance <- Eigenvalues / sum(Eigenvalues)

3 Differential Expression

This topic might be of interest to people who work with transcriptomics data specifically, but it is a fun dataset to explore even if you dont work with this kind of data. There are 3 files similar to Time_t2_vs_t0.txt that basically has the list of genes that are differentially expressed in time-pointt2 vs t0. The other 2 files Time_t6_vs_t0.txt and Time_t24_vs_t0.txt represents the comparisons t6 vs t0 and t24 vs t0 respectively. Let us take a quick look at one of these files:

t2_vs_t0 <- read.table("../../data/Time_t2_vs_t0.txt", sep = "\t", header = TRUE, row.names = 1)
head(t2_vs_t0)

This table was generated from a differential expression analysis using DESeq2. These variables from DESeq2 are explained as follows:

  • baseMean: The average of the normalized counts for all samples, a measure of the average expression level of a gene.
  • log2FoldChange: The log2-transformed fold change between two conditions, indicating the magnitude and direction of differential expression. In this particular case, a +ve value would indicate upregulation of the gene in t2 and a -ve value would indicate downregulation of the gene in t2.
  • lfcSE: The standard error of the log2 fold change, representing the variability or uncertainty in the fold change estimate.
  • stat: The test statistic used to determine differential expression, typically a Wald statistic.
  • pvalue: The p-value for the hypothesis test, indicating the probability of observing the data under the null hypothesis of no differential expression.
  • padj: The adjusted p-value (e.g., using the Benjamini-Hochberg method) to control for false discovery rate (FDR) in multiple testing.

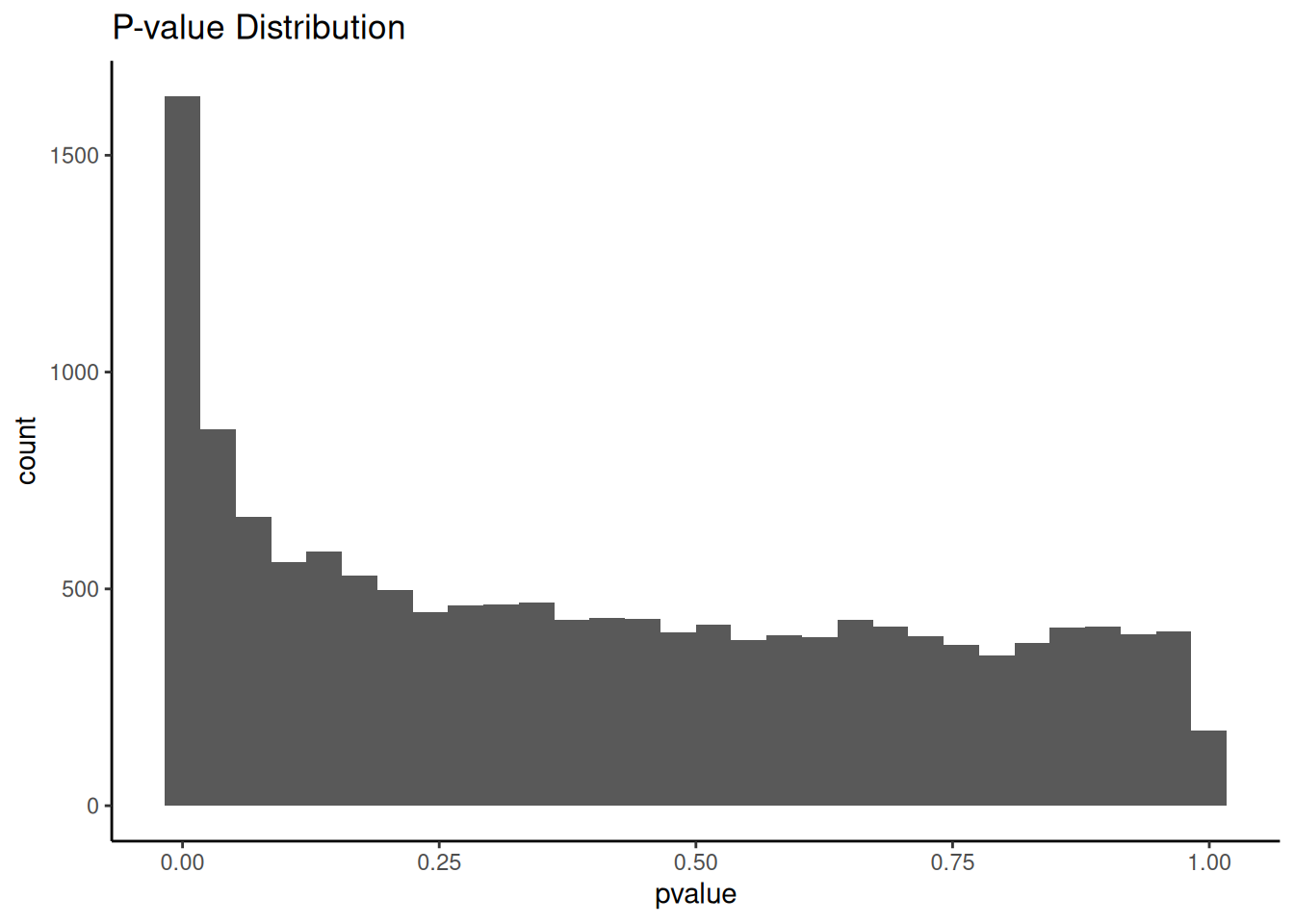
When you do these kinds of analysis that involves a lot of parameters, one of the first thing you should do is to look at the distribution of the unadjusted p-values.

t2_vs_t0 %>%
  ggplot(aes(x = pvalue)) +
  geom_histogram() +
  theme_classic() +
  ggtitle("P-value Distribution")

The distribution looks what is expected of an anlysis like differential gene-expression.

Tip

If you are interested more in understanding the distribution of p-values, you can read about the possible different outcomes and their reasoning here.

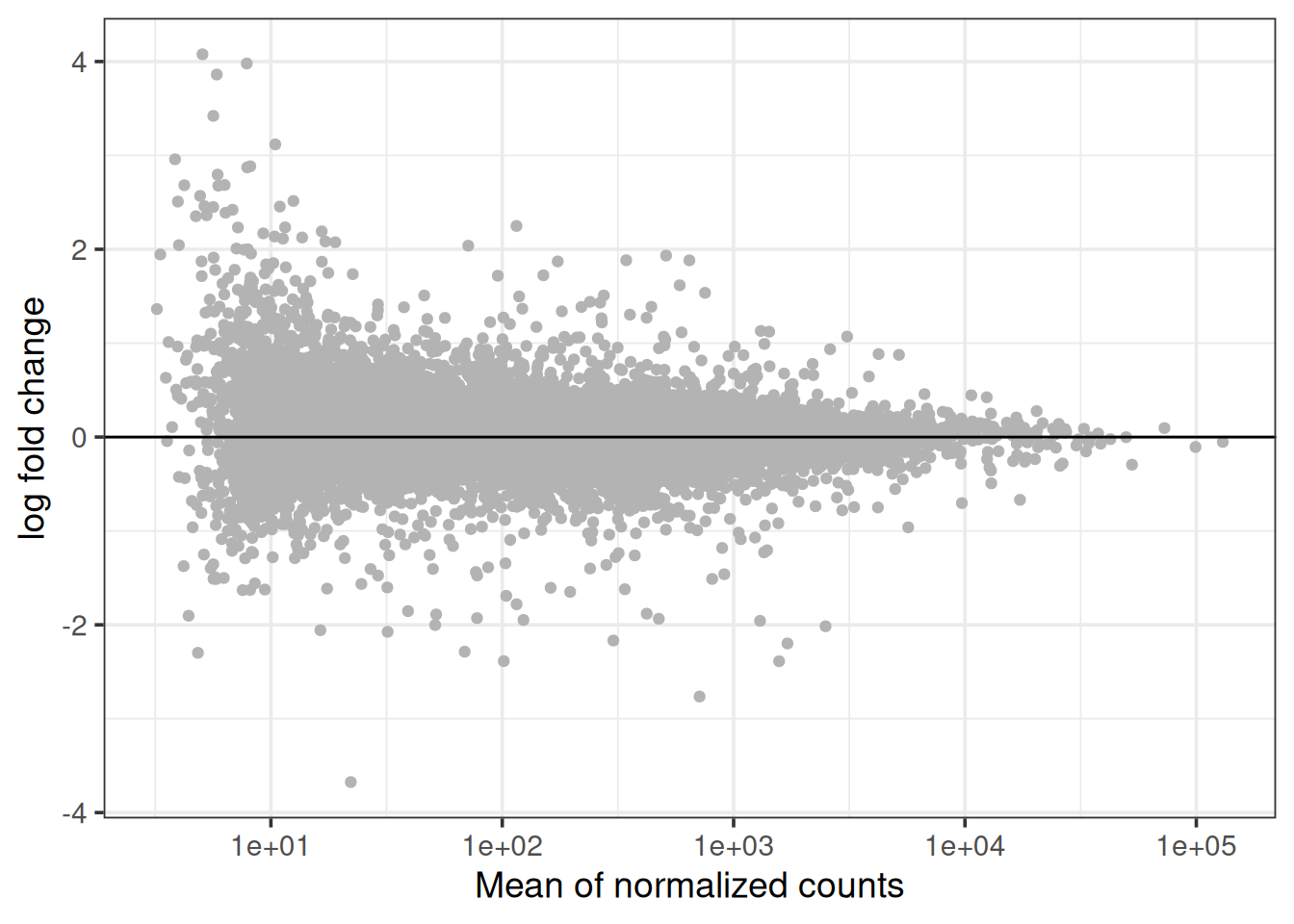
3.1 MA plot.

The MA plot shows the distribution of mean expression vs log fold change for all genes.

t2_vs_t0 %>%
  ggplot(aes(x = baseMean, y = log2FoldChange)) +
  geom_point(color = "grey70") +
  geom_hline(yintercept = 0) +
  scale_x_log10("Mean of normalized counts") +
  ylab("log fold change") +
  theme_bw(base_size = 14)

Try to think about each of the line of code that was used to generate the plot and what it’s function is. At the moment, the plot contains all genes that are colored the with same grey scale.

You can read more about MA plot and what it means here

3.2 Exercise II

Task 2.1

This plot would be even more informative when you color the significant genes differently. Would you be able to generate that plot?

Tip

You can filter the data that has adjusted p-value < 0.05 and plot the points with a different color.

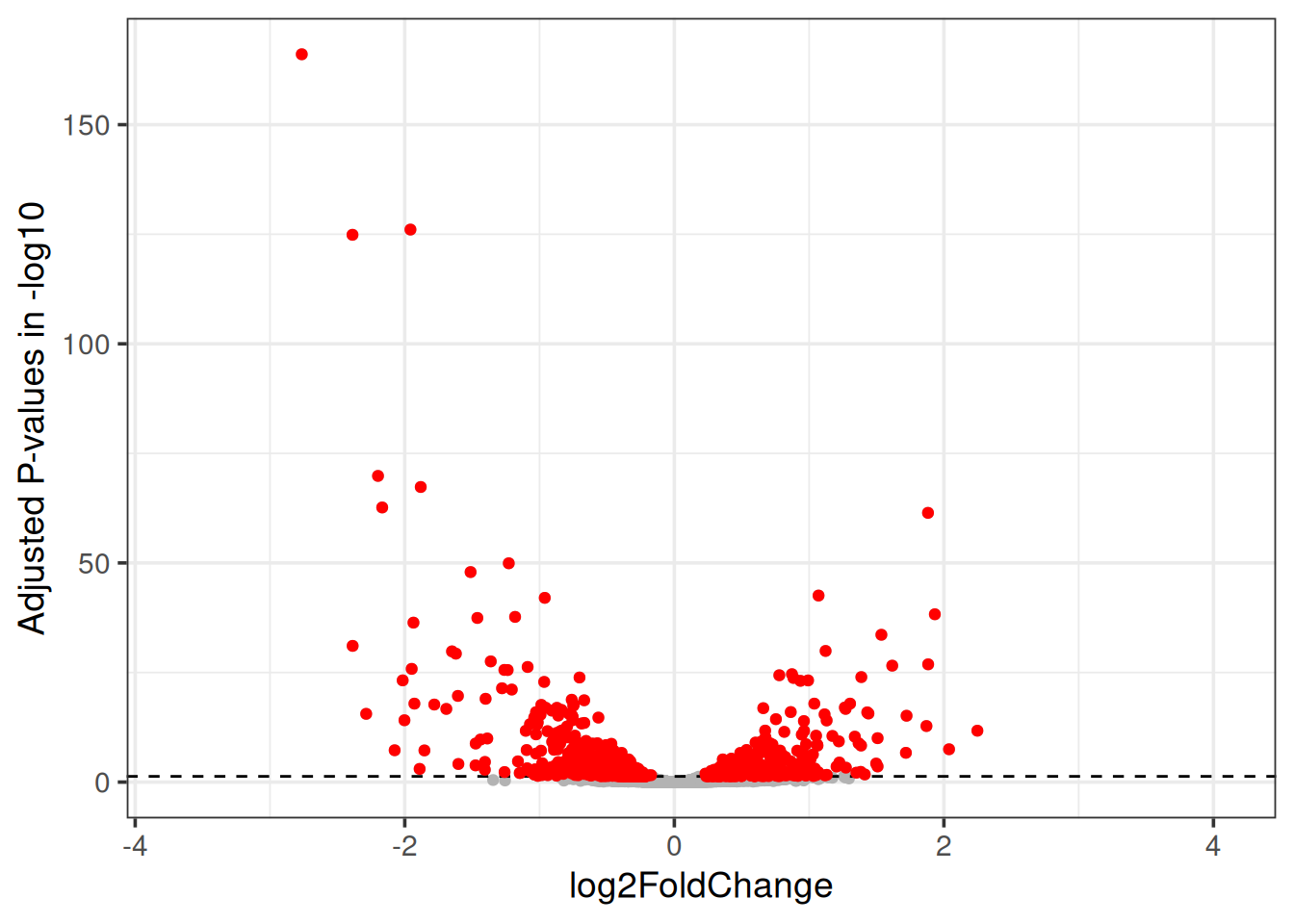
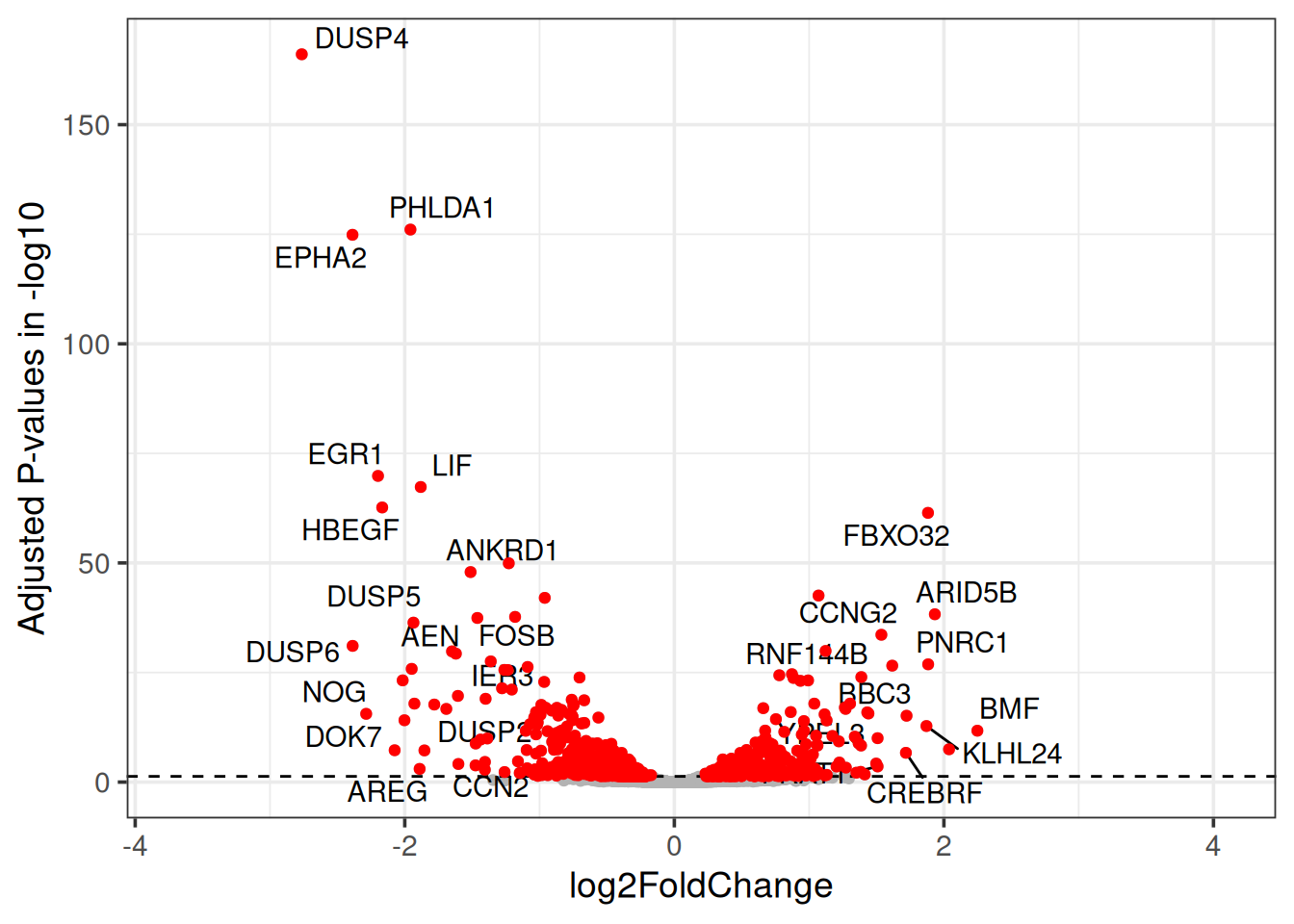
3.3 Volcano plot

Similar to MA plot, Volcano plot indicates the relation between the adjusted p-values and the log fold change. The adjusted p-value is transformed with -log10 on the y-axis, so that the smallest p-values appears at the top of the plot. The log2FoldCange values are plotted as they are on the x-axis, so that the down-regulated genes are on the left of the x-axis (-ve values) and the up-regulated genes are on the right of the x-axis (+ve values).

t2_vs_t0 %>%
  ggplot(aes(x = log2FoldChange, y = -log10(padj))) +
  geom_point(color = "grey70") +
  geom_hline(yintercept = 1.3, linetype = 2) +
  geom_point(data=filter(t2_vs_t0, padj < 0.05), color = "red") +
  ylab("Adjusted P-values in -log10") +
  theme_bw(base_size = 14)

You can read more about Volcano plot and what it means here

3.4 Exercise II

Task 2.2

Try to code the plot below:

Note

You can find the gene name information in the file data/human_biomaRt_annotation.csv.

Tip

You can filter the data that has adjusted p-value < 0.05 and log2FoldChange > ±1.5 for the text part and use geom_text_repel().

4 Heatmap

4.1 pheatmap

4.1.1 Samples

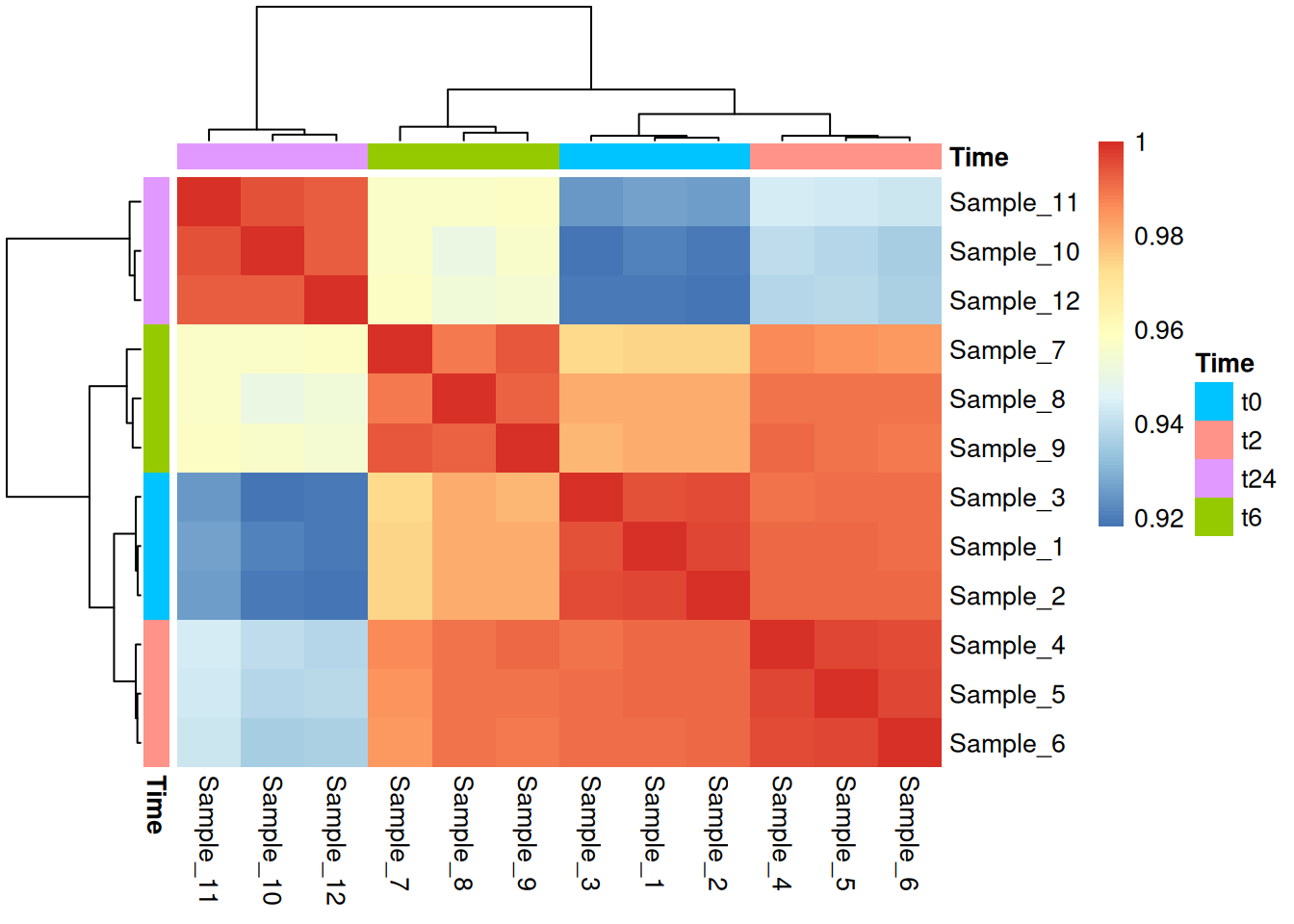
For heatmap, let us look into pheatmap library which is not part of ggplot, but it is a well known package for building heatmaps. It contains a lot of internal aesthetics that you can add that are very informative and intuitive. Let us first start with making a correlation matrix and plot it.

vst_cor <- as.matrix(cor(gc_vst, method="spearman"))
library(pheatmap)

pheatmap(vst_cor,border_color=NA,annotation_col=md[,"Time",drop=F],
         annotation_row=md[,"Time",drop=F],annotation_legend=T)

Note

If you get a gpar() error, this is due to the reason that the metadata table you provide here does not have the sample ids as rownames. pheatmap maps the meta-data to the count data using rownames

Now, this is based on a correlation matrix where you have a very simple square matrix with samples and their correlations to each to each other. Now let us look into how we can make a heatmap from an expression dataset.

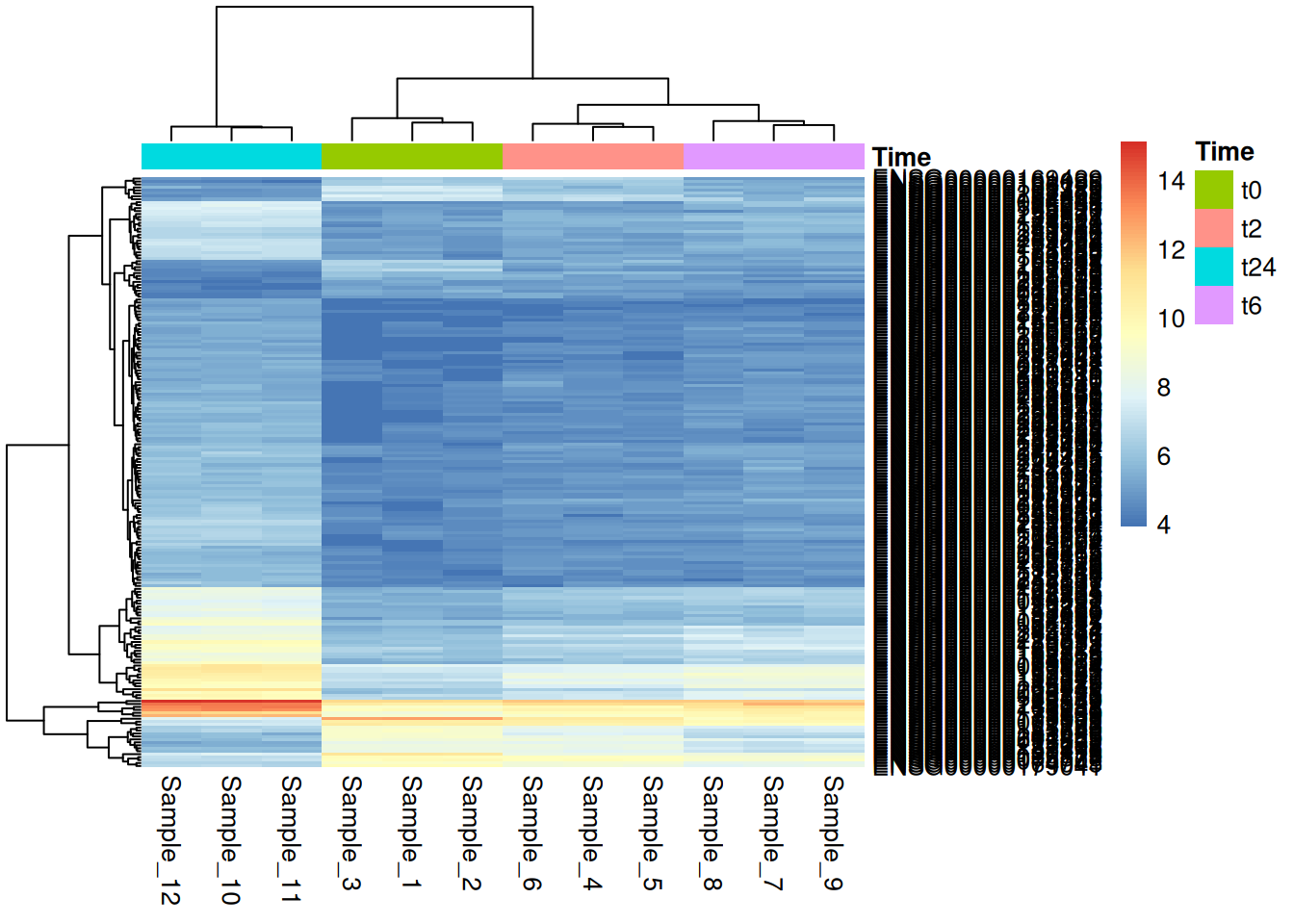
4.1.2 Genes

For this we will use the dataset: Time_t24_vs_t0.txt here that basically has the list of genes that are differentially expressed in t24 vs t0 and we would like to visualize this in an heatmap. To be more precise, we take the top 200 genes (based on fold change) with adjusted p-value < 0.001. We use just these 200, for the sake of visualization. Let us take the t24 vs t0 here as these are most different based on our PCA.

t24_vs_t0 <- read.table("../../data/Time_t24_vs_t0.txt", sep = "\t", header = TRUE, row.names = 1)

diff_t24_vs_t0 <- t24_vs_t0 %>% 
  rownames_to_column('gene') %>%
  filter(padj < 0.001) %>%
  arrange(desc(abs(log2FoldChange))) %>%
  head(200)

hmap_t24_t0 <- subset(gc_vst, rownames(gc_vst) %in% diff_t24_vs_t0$gene)

pheatmap(hmap_t24_t0, border_color=NA, annotation_col=md[,"Time",drop=F], annotation_row=NULL, annotation_legend=T)

Further, we can also customize using the pheatmap and also use the continous color options we talked about in the earlier sections.

library(wesanderson)
md$Time <- factor(md$Time, levels = c("t0","t2","t6","t24"))

pheatmap(hmap_t24_t0, color = wes_palette("Moonrise3", 100, type = "continuous"), border_color=NA, annotation_col=md[,"Time",drop=F], annotation_row=NULL, annotation_legend=T, show_rownames = FALSE, fontsize = 14)

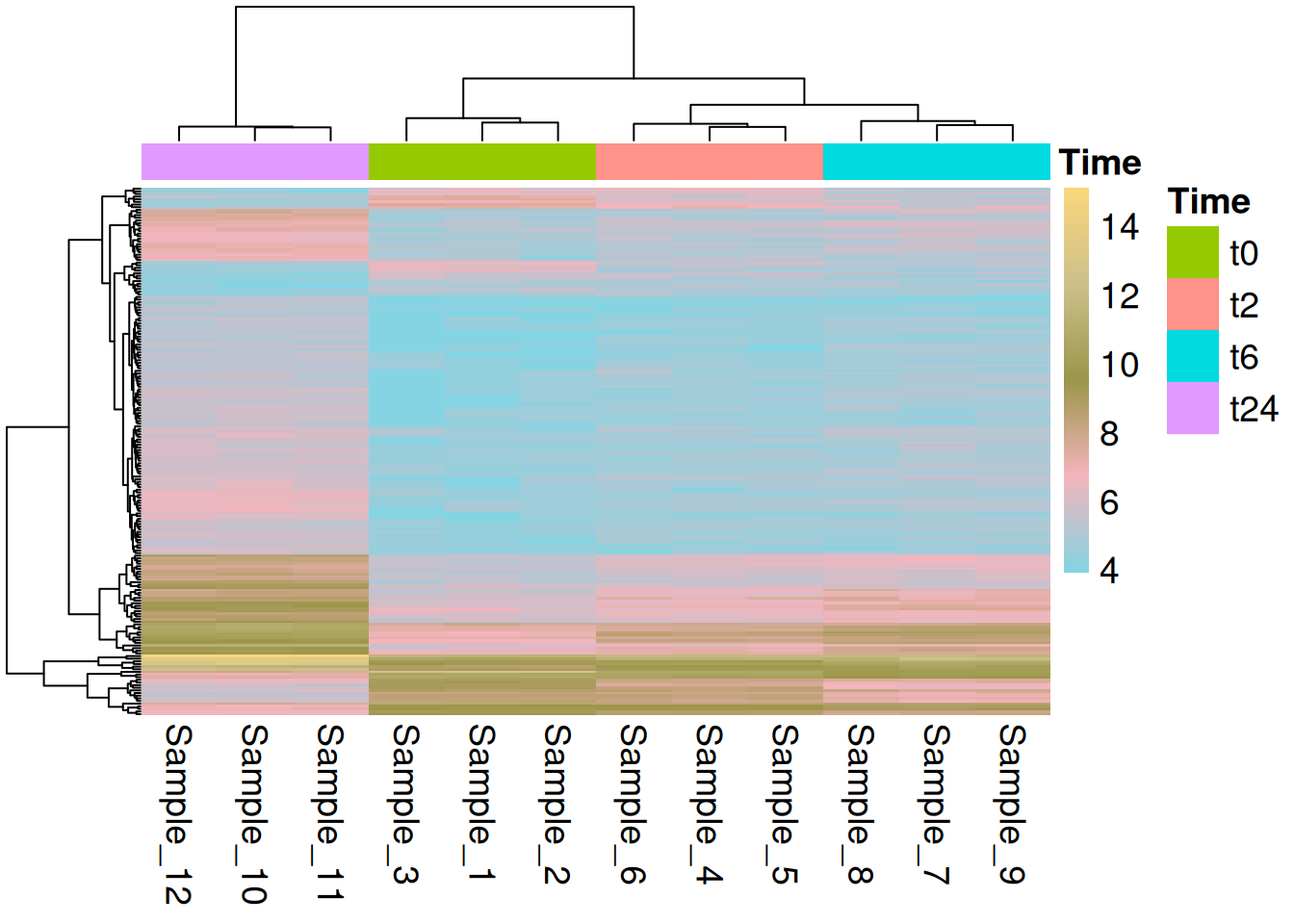
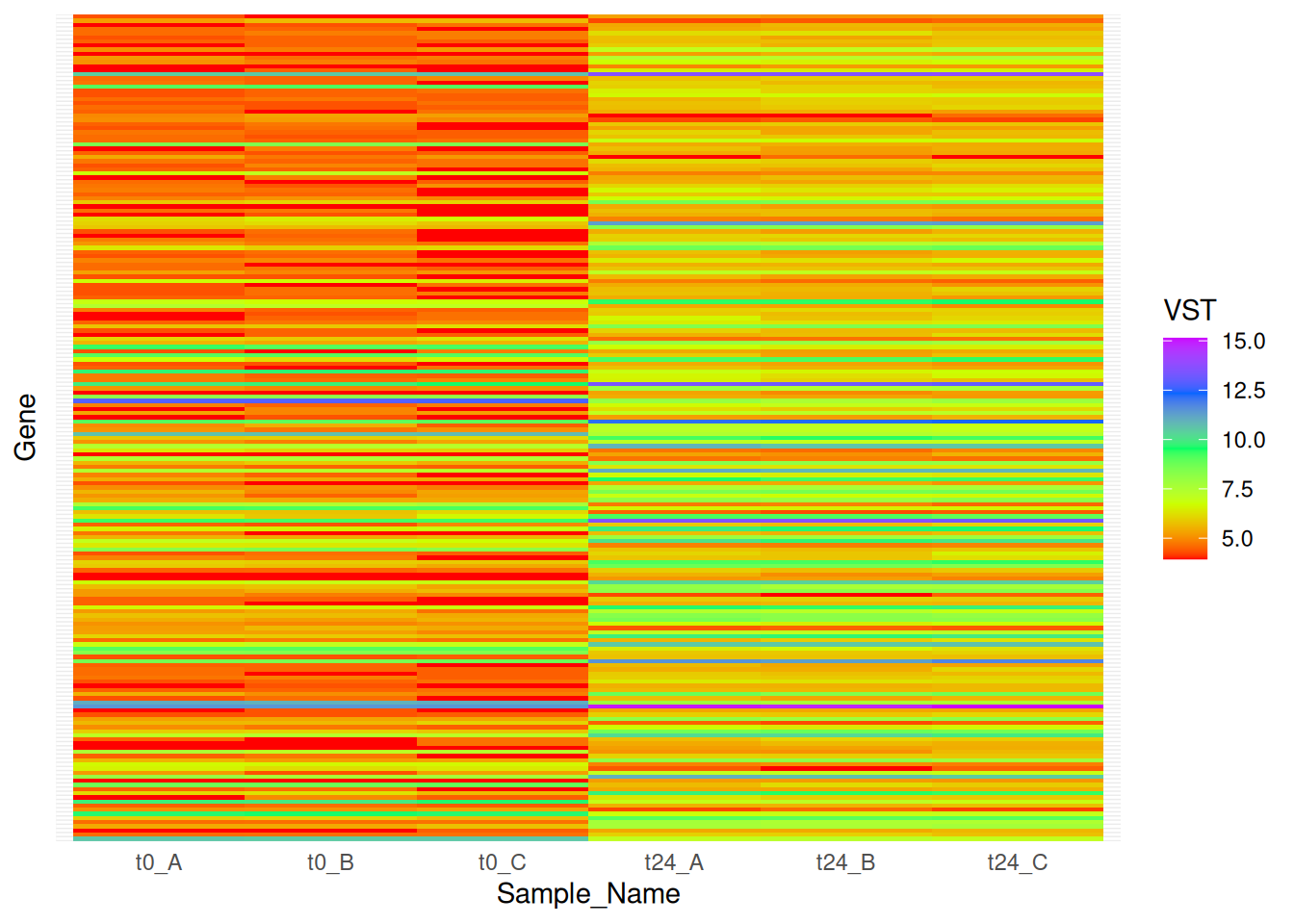
4.2 ggplot

We can use geom_tile() from ggplot to make heatmaps. The ggplot based heatmaps are, as we have seen for other cases, much more easier to customize.

hmap_t24_t0_long <- hmap_t24_t0 %>%
  rownames_to_column(var = "Gene") %>%
  gather(Sample_ID, VST, -Gene) %>% 
  full_join(md, by = "Sample_ID")  

hmap_t24_t0_long$Sample_Name <- factor(hmap_t24_t0_long$Sample_Name, levels = 
                                        c("t0_A","t0_B","t0_C","t2_A","t2_B","t2_C","t6_A","t6_B","t6_C","t24_A","t24_B","t24_C"))
hmap_t24_t0_long$Time <- factor(hmap_t24_t0_long$Time, levels = c("t0","t2","t6","t24"))
hmap_t24_t0_long$Replicate <- factor(hmap_t24_t0_long$Replicate, levels = c("A","B","C"))
hmap_t24_t0_long$Gene <- factor(hmap_t24_t0_long$Gene, levels = row.names(hmap_t24_t0))

ggplot(hmap_t24_t0_long) +
  geom_tile(aes(x = Sample_Name, y = Gene, fill = VST)) +
  scale_fill_gradientn(colours = rainbow(5)) +
  scale_x_discrete(limits = c("t0_A","t0_B","t0_C","t24_A","t24_B","t24_C")) +
  theme(axis.text.y = element_blank(), axis.ticks = element_blank())

As you can see and compare that the heatmaps produced by pheatmap are way better than ggplot.