import numpy as np
import pandas as pd
import scanpy as sc
import matplotlib.pyplot as plt
import warnings
import os
import urllib.request
warnings.simplefilter(action="ignore", category=Warning)
# verbosity: errors (0), warnings (1), info (2), hints (3)
sc.settings.verbosity = 3
# sc.logging.print_versions()
sc.settings.set_figure_params(dpi=80)
Note
Code chunks run Python commands unless it starts with %%bash, in which case, those chunks run shell commands.
1 Data preparation
First, let’s load all necessary libraries and the QC-filtered dataset from the previous step.
# download pre-computed data if missing or long compute
fetch_data = True
# url for source and intermediate data
path_data = "https://export.uppmax.uu.se/naiss2023-23-3/workshops/workshop-scrnaseq"
path_results = "data/covid/results"
if not os.path.exists(path_results):
os.makedirs(path_results, exist_ok=True)
path_file = "data/covid/results/scanpy_covid_qc.h5ad"
# if fetch_data is false and path_file doesn't exist
if fetch_data and not os.path.exists(path_file):
urllib.request.urlretrieve(os.path.join(
path_data, 'covid/results/scanpy_covid_qc.h5ad'), path_file)
adata = sc.read_h5ad(path_file)
adataAnnData object with n_obs × n_vars = 7222 × 19468
obs: 'type', 'sample', 'batch', 'n_genes_by_counts', 'total_counts', 'total_counts_mt', 'pct_counts_mt', 'total_counts_ribo', 'pct_counts_ribo', 'total_counts_hb', 'pct_counts_hb', 'percent_mt2', 'n_counts', 'n_genes', 'percent_chrY', 'XIST-counts', 'S_score', 'G2M_score', 'phase', 'doublet_scores', 'predicted_doublets', 'doublet_info'
var: 'gene_ids', 'feature_types', 'genome', 'mt', 'ribo', 'hb', 'n_cells_by_counts', 'mean_counts', 'pct_dropout_by_counts', 'total_counts', 'n_cells'
uns: 'doublet_info_colors', 'hvg', 'log1p', 'neighbors', 'pca', 'phase_colors', 'sample_colors', 'umap'
obsm: 'X_pca', 'X_umap'
obsp: 'connectivities', 'distances'Before variable gene selection we need to normalize and log transform the data. Then store the full matrix in the raw slot before doing variable gene selection.
# normalize to depth 10 000
sc.pp.normalize_per_cell(adata, counts_per_cell_after=1e4)
# log transform
sc.pp.log1p(adata)
# store normalized counts in the raw slot,
# we will subset adata.X for variable genes, but want to keep all genes matrix as well.
adata.raw = adata
adatanormalizing by total count per cell
finished (0:00:00): normalized adata.X and added 'n_counts', counts per cell before normalization (adata.obs)
WARNING: adata.X seems to be already log-transformed.AnnData object with n_obs × n_vars = 7222 × 19468
obs: 'type', 'sample', 'batch', 'n_genes_by_counts', 'total_counts', 'total_counts_mt', 'pct_counts_mt', 'total_counts_ribo', 'pct_counts_ribo', 'total_counts_hb', 'pct_counts_hb', 'percent_mt2', 'n_counts', 'n_genes', 'percent_chrY', 'XIST-counts', 'S_score', 'G2M_score', 'phase', 'doublet_scores', 'predicted_doublets', 'doublet_info'
var: 'gene_ids', 'feature_types', 'genome', 'mt', 'ribo', 'hb', 'n_cells_by_counts', 'mean_counts', 'pct_dropout_by_counts', 'total_counts', 'n_cells'
uns: 'doublet_info_colors', 'hvg', 'log1p', 'neighbors', 'pca', 'phase_colors', 'sample_colors', 'umap'
obsm: 'X_pca', 'X_umap'
obsp: 'connectivities', 'distances'2 Feature selection
We first need to define which features/genes are important in our dataset to distinguish cell types. For this purpose, we need to find genes that are highly variable across cells, which in turn will also provide a good separation of the cell clusters.
# compute variable genes
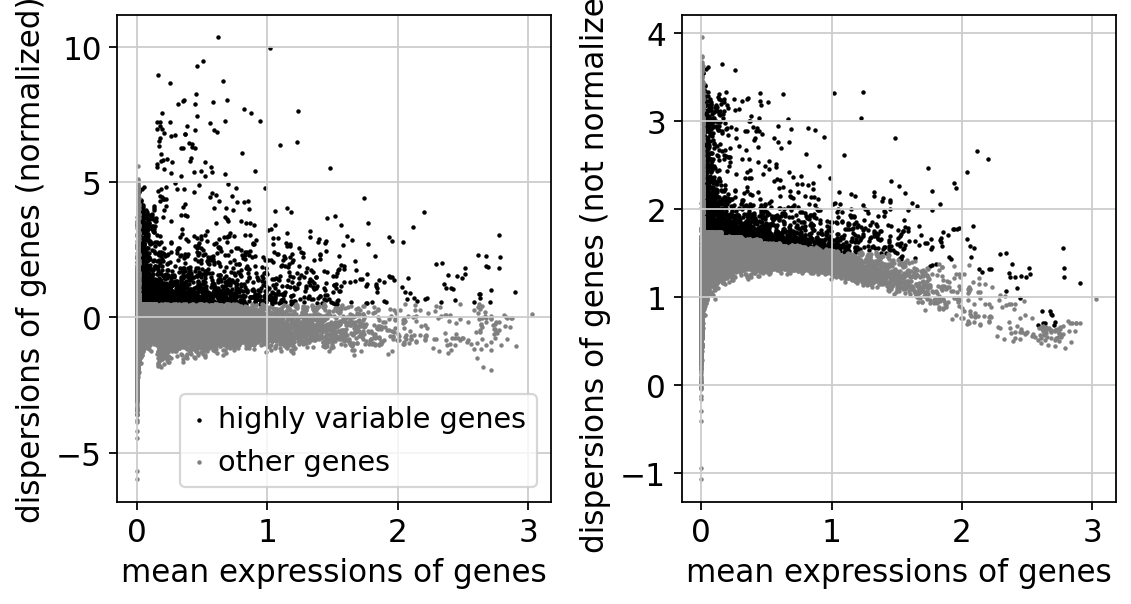
sc.pp.highly_variable_genes(adata, min_mean=0.0125, max_mean=3, min_disp=0.5)
print("Highly variable genes: %d"%sum(adata.var.highly_variable))
#plot variable genes
sc.pl.highly_variable_genes(adata)
# subset for variable genes in the dataset
adata = adata[:, adata.var['highly_variable']]extracting highly variable genes
finished (0:00:01)
--> added
'highly_variable', boolean vector (adata.var)
'means', float vector (adata.var)
'dispersions', float vector (adata.var)
'dispersions_norm', float vector (adata.var)
Highly variable genes: 2626
3 Z-score transformation
Now that the genes have been selected, we now proceed with PCA. Since each gene has a different expression level, it means that genes with higher expression values will naturally have higher variation that will be captured by PCA. This means that we need to somehow give each gene a similar weight when performing PCA (see below). The common practice is to center and scale each gene before performing PCA. This exact scaling called Z-score normalization is very useful for PCA, clustering and plotting heatmaps. Additionally, we can use regression to remove any unwanted sources of variation from the dataset, such as cell cycle, sequencing depth, percent mitochondria etc. This is achieved by doing a generalized linear regression using these parameters as co-variates in the model. Then the residuals of the model are taken as the regressed data. Although perhaps not in the best way, batch effect regression can also be done here. By default, variables are scaled in the PCA step and is not done separately. But it could be achieved by running the commands below:
#run this line if you get the "AttributeError: swapaxes not found"
# adata = adata.copy()
# regress out unwanted variables
sc.pp.regress_out(adata, ['total_counts', 'pct_counts_mt'])
# scale data, clip values exceeding standard deviation 10.
sc.pp.scale(adata, max_value=10)regressing out ['total_counts', 'pct_counts_mt']
sparse input is densified and may lead to high memory use
finished (0:00:56)4 PCA
Performing PCA has many useful applications and interpretations, which much depends on the data used. In the case of single-cell data, we want to segregate samples based on gene expression patterns in the data.
To run PCA, you can use the function pca().
sc.tl.pca(adata, svd_solver='arpack')computing PCA
on highly variable genes
with n_comps=50
finished (0:00:07)We then plot the first principal components.
# plot more PCS
sc.pl.pca(adata, color='sample', components = ['1,2','3,4','5,6','7,8'], ncols=2)
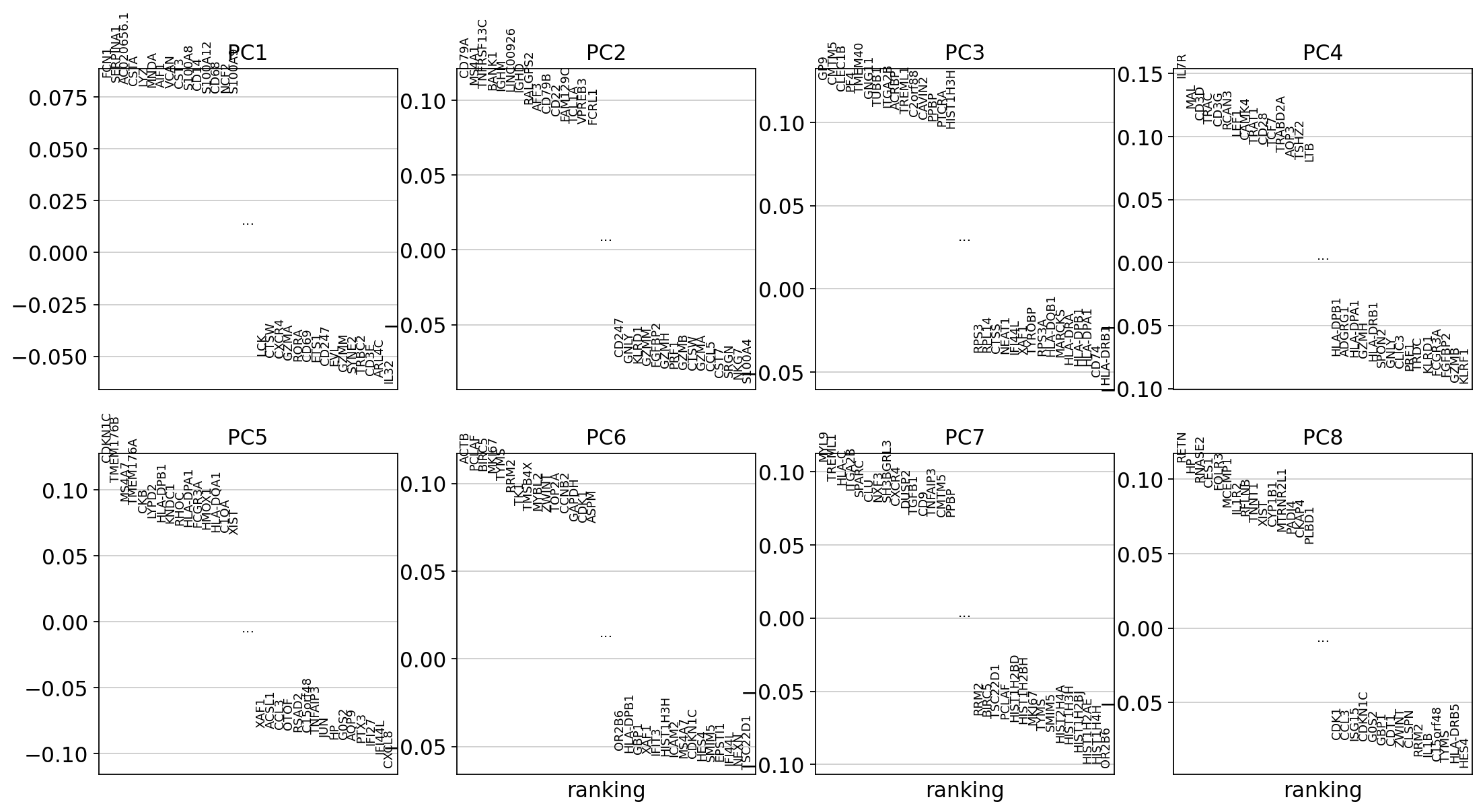
To identify genes that contribute most to each PC, one can retrieve the loading matrix information.
#Plot loadings
sc.pl.pca_loadings(adata, components=[1,2,3,4,5,6,7,8])
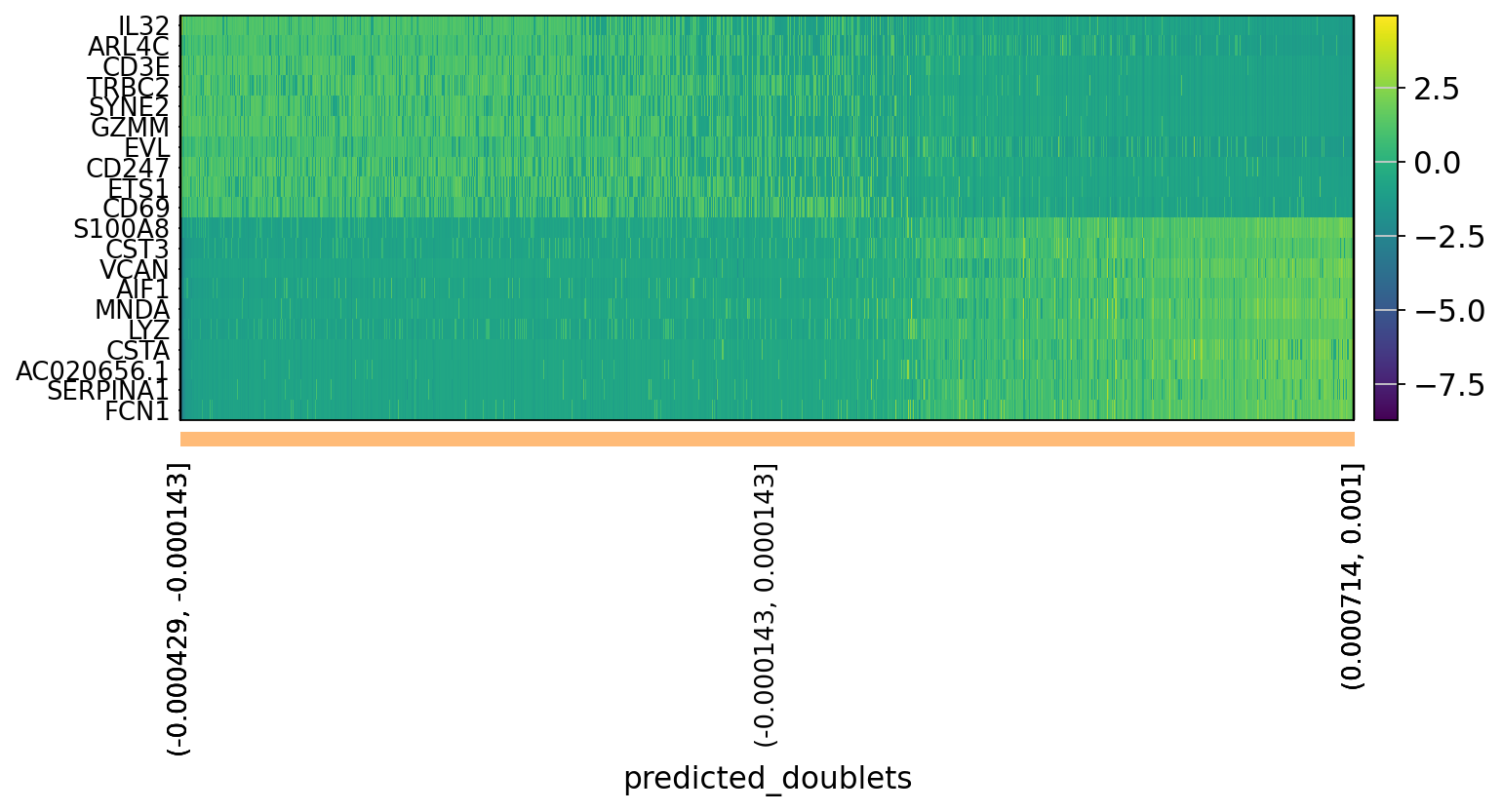
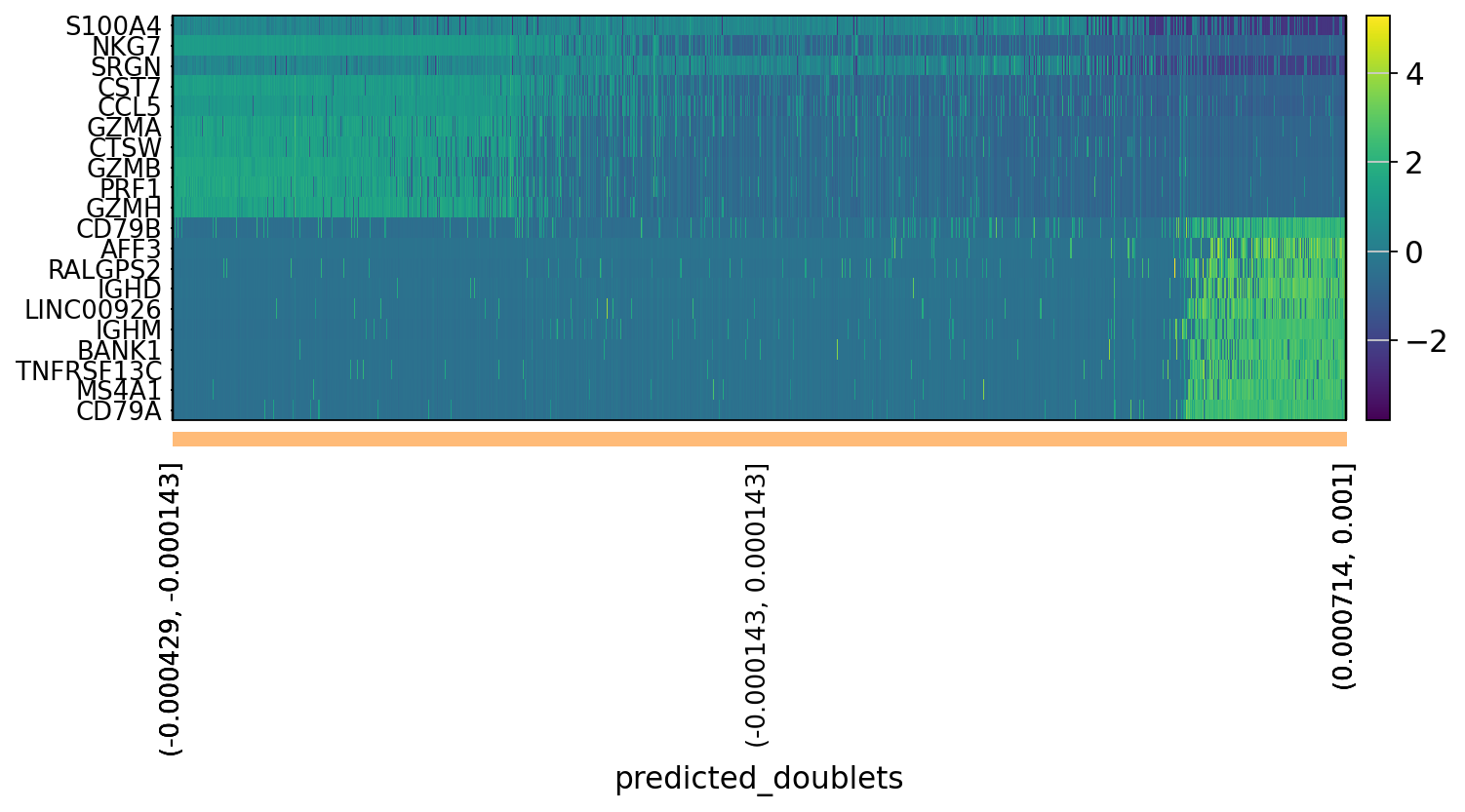
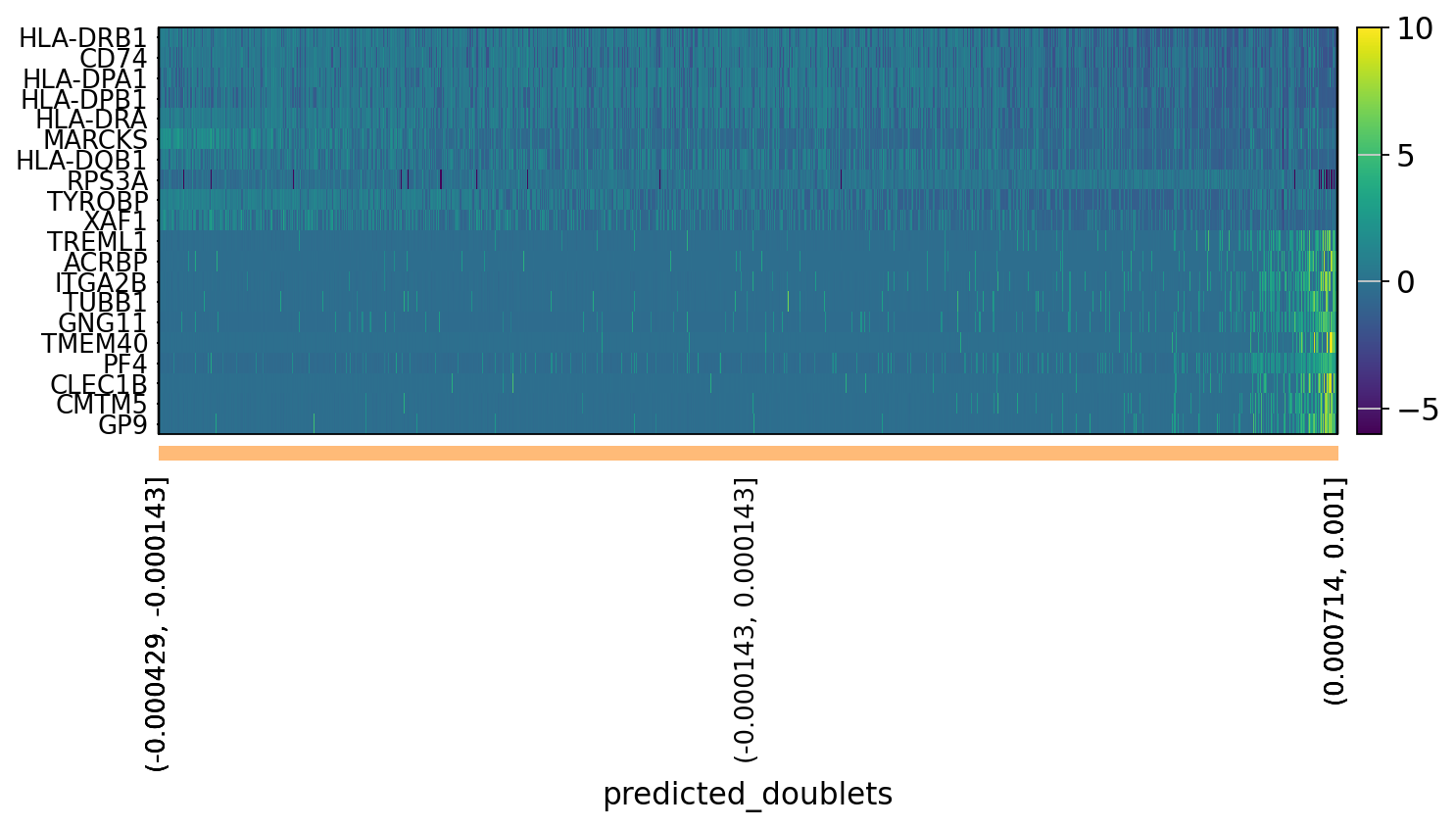
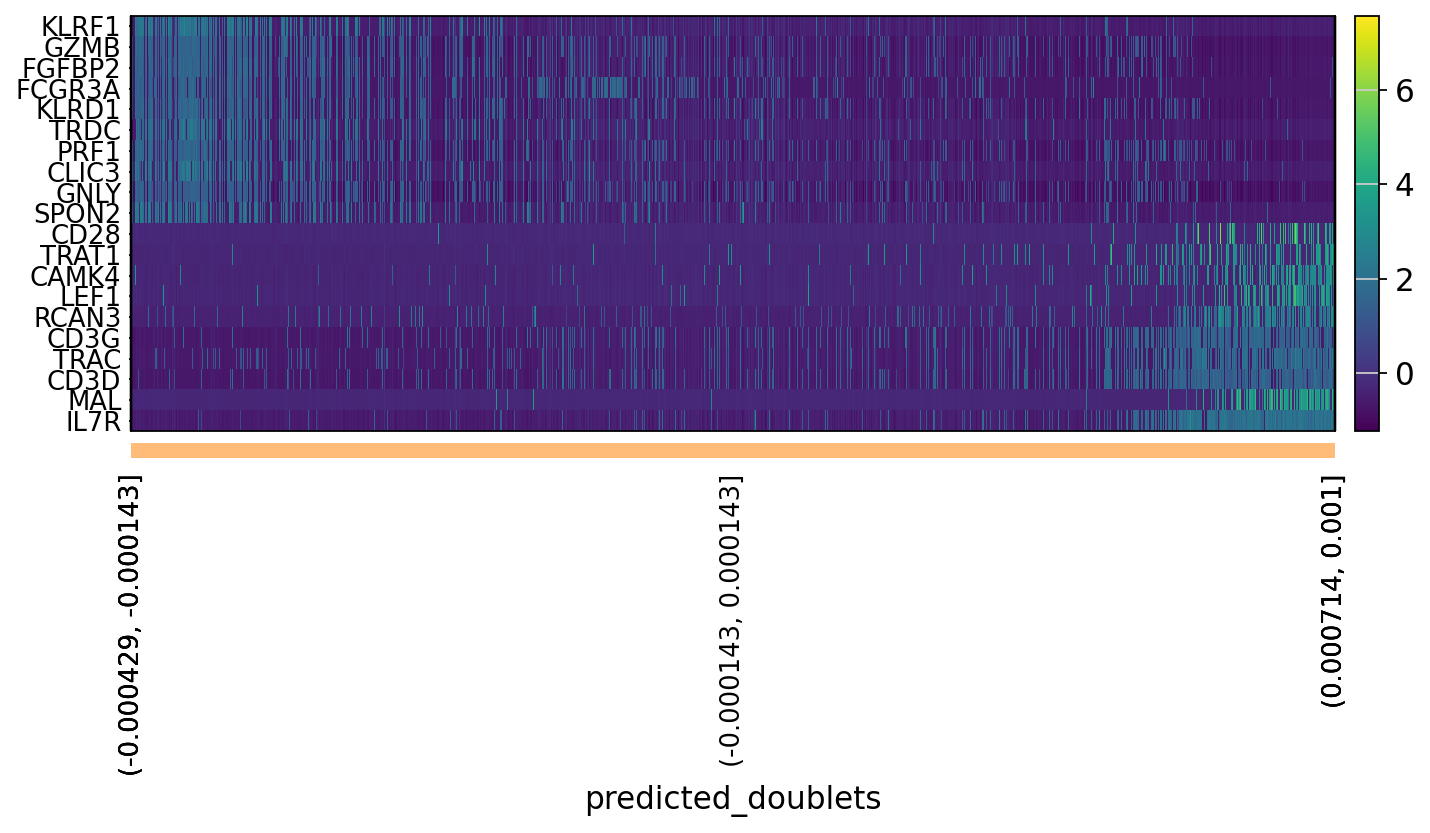
# OBS! only plots the positive axes genes from each PC!!
The function to plot loading genes only plots genes on the positive axes. Instead plot as a heatmaps, with genes on both positive and negative side, one per pc, and plot their expression amongst cells ordered by their position along the pc.
# adata.obsm["X_pca"] is the embeddings
# adata.uns["pca"] is pc variance
# adata.varm['PCs'] is the loadings
genes = adata.var['gene_ids']
for pc in [1,2,3,4]:
g = adata.varm['PCs'][:,pc-1]
o = np.argsort(g)
sel = np.concatenate((o[:10],o[-10:])).tolist()
emb = adata.obsm['X_pca'][:,pc-1]
# order by position on that pc
tempdata = adata[np.argsort(emb),]
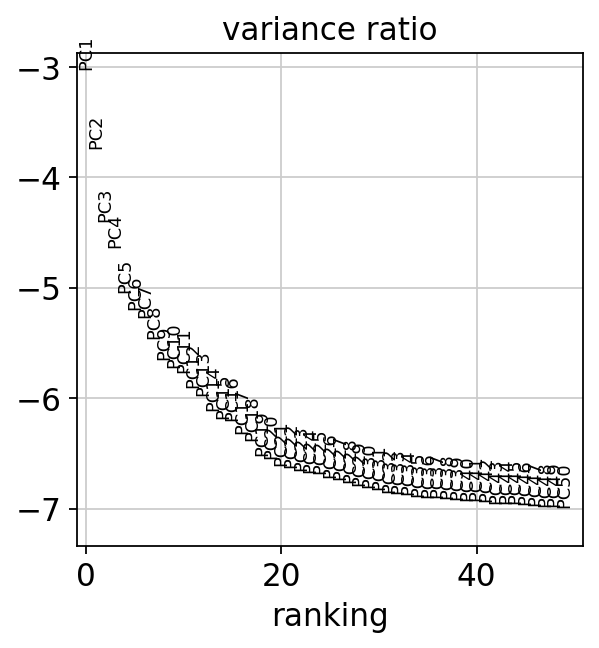
sc.pl.heatmap(tempdata, var_names = genes[sel].index.tolist(), groupby='predicted_doublets', swap_axes = True, use_raw=False)
We can also plot the amount of variance explained by each PC.
sc.pl.pca_variance_ratio(adata, log=True, n_pcs = 50)
Based on this plot, we can see that the top 8 PCs retain a lot of information, while other PCs contain progressively less. However, it is still advisable to use more PCs since they might contain information about rare cell types (such as platelets and DCs in this dataset)
5 tSNE
We will now run BH-tSNE.
sc.tl.tsne(adata, n_pcs = 30)computing tSNE
using 'X_pca' with n_pcs = 30
using sklearn.manifold.TSNE
finished: added
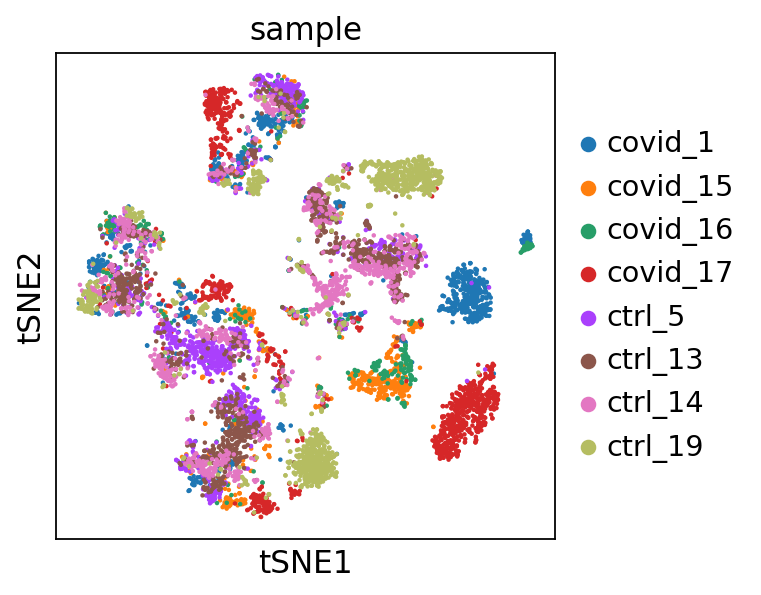
'X_tsne', tSNE coordinates (adata.obsm) (0:00:23)We plot the tSNE scatterplot colored by dataset. We can clearly see the effect of batches present in the dataset.
sc.pl.tsne(adata, color='sample')
6 UMAP
The UMAP implementation in SCANPY uses a neighborhood graph as the distance matrix, so we need to first calculate the graph.
sc.pp.neighbors(adata, n_pcs = 30, n_neighbors = 20)computing neighbors
using 'X_pca' with n_pcs = 30
finished: added to `.uns['neighbors']`
`.obsp['distances']`, distances for each pair of neighbors
`.obsp['connectivities']`, weighted adjacency matrix (0:00:14)We can now run UMAP for cell embeddings.
sc.tl.umap(adata)
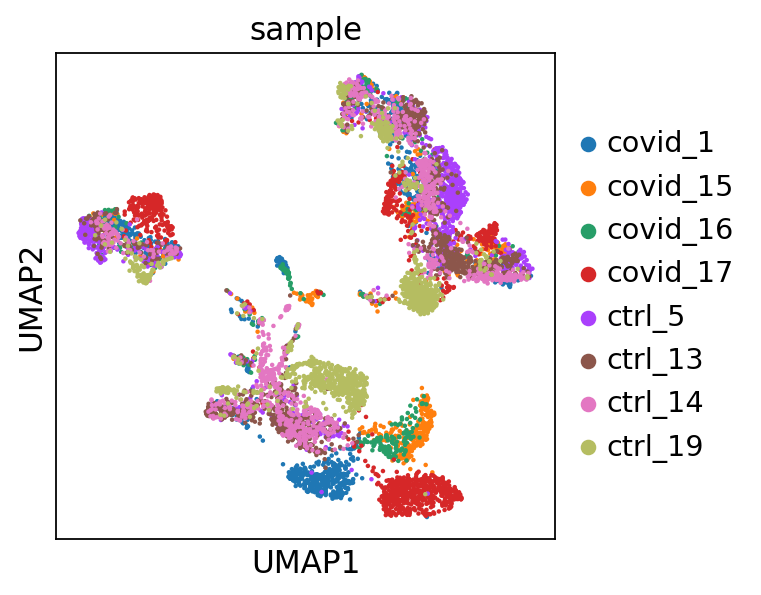
sc.pl.umap(adata, color='sample')computing UMAP
finished: added
'X_umap', UMAP coordinates (adata.obsm) (0:00:13)
UMAP is plotted colored per dataset. Although less distinct as in the tSNE, we still see quite an effect of the different batches in the data.
# run with 10 components, save to a new object so that the umap with 2D is not overwritten.
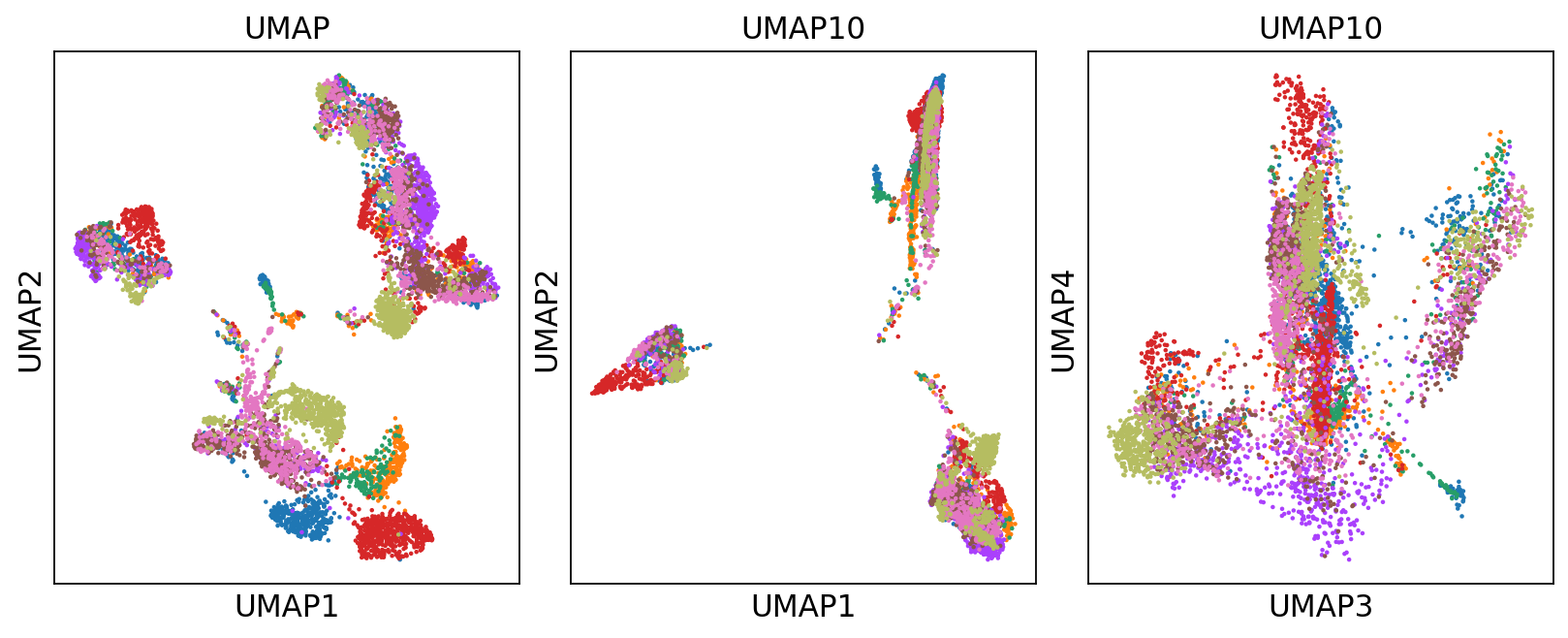
umap10 = sc.tl.umap(adata, n_components=10, copy=True)
fig, axs = plt.subplots(1, 3, figsize=(10, 4), constrained_layout=True)
sc.pl.umap(adata, color='sample', title="UMAP",
show=False, ax=axs[0], legend_loc=None)
sc.pl.umap(umap10, color='sample', title="UMAP10", show=False,
ax=axs[1], components=['1,2'], legend_loc=None)
sc.pl.umap(umap10, color='sample', title="UMAP10",
show=False, ax=axs[2], components=['3,4'], legend_loc=None)
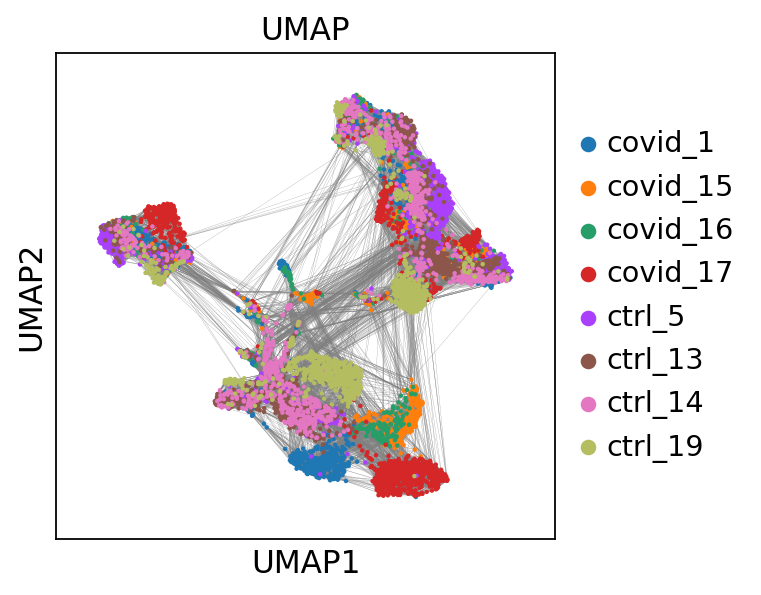
# we can also plot the umap with neighbor edges
sc.pl.umap(adata, color='sample', title="UMAP", edges=True)computing UMAP
finished: added
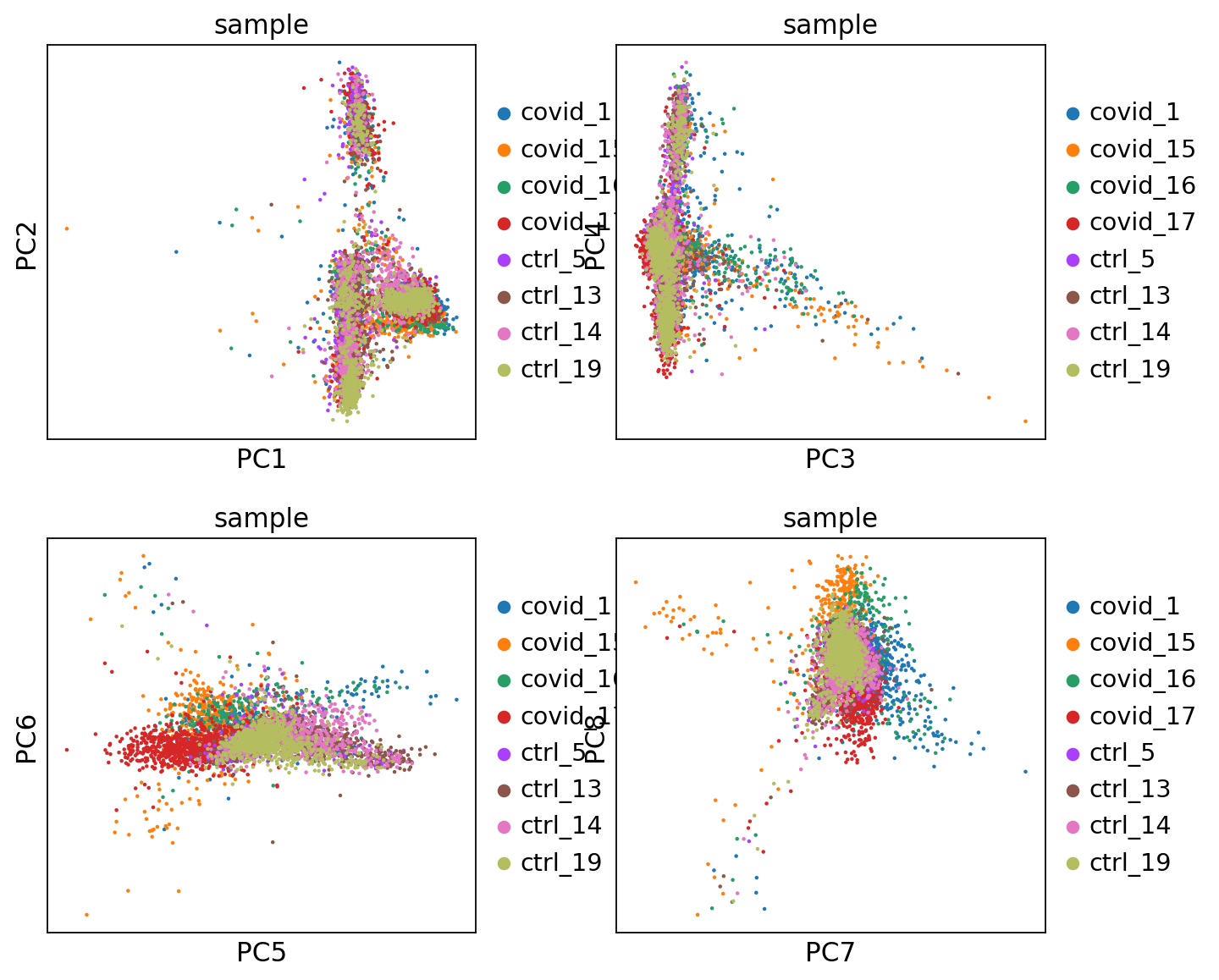
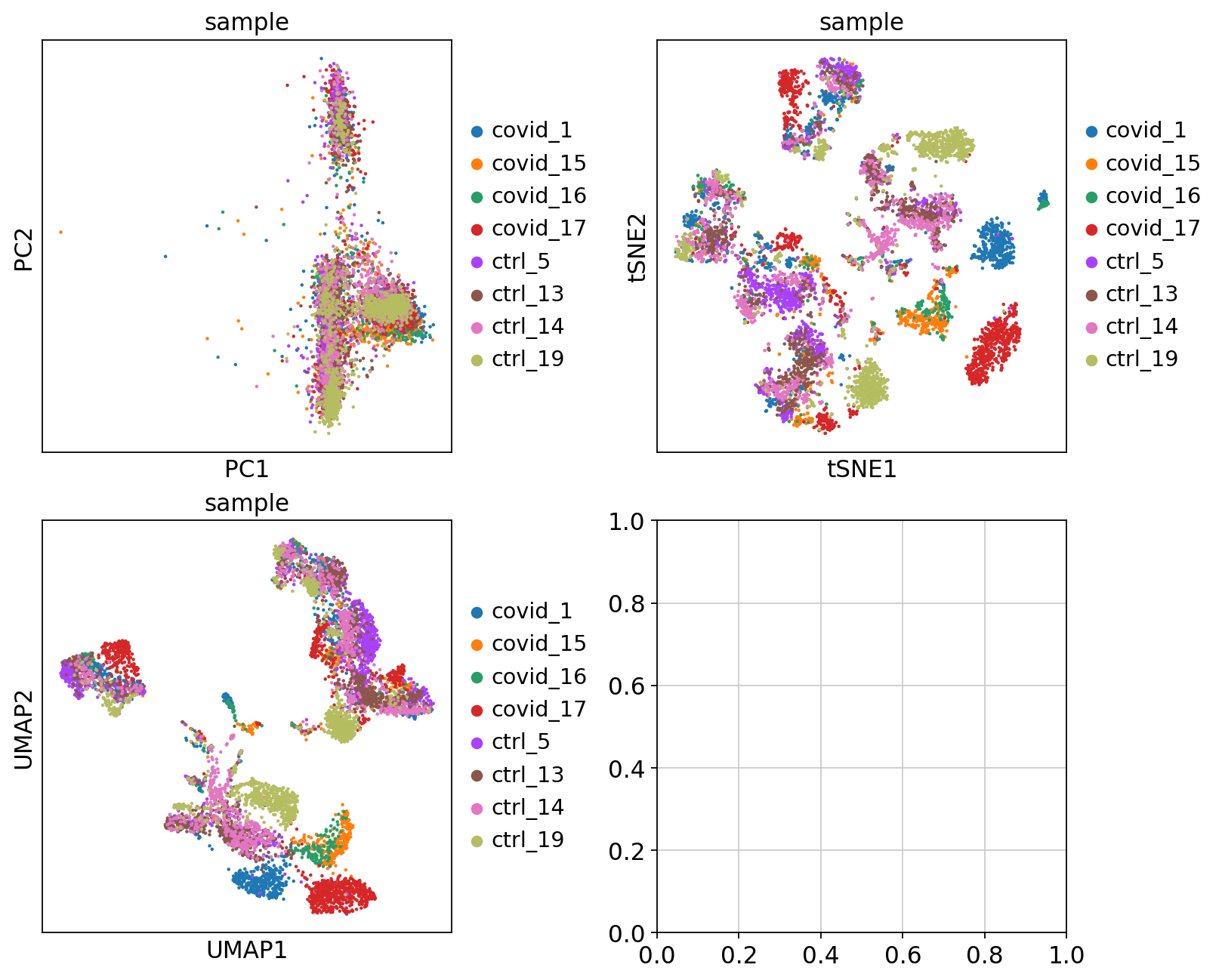
'X_umap', UMAP coordinates (adata.obsm) (0:00:16)
We can now plot PCA, UMAP and tSNE side by side for comparison. Have a look at the UMAP and tSNE. What similarities/differences do you see? Can you explain the differences based on what you learned during the lecture? Also, we can conclude from the dimensionality reductions that our dataset contains a batch effect that needs to be corrected before proceeding to clustering and differential gene expression analysis.
fig, axs = plt.subplots(2, 2, figsize=(10, 8), constrained_layout=True)
sc.pl.pca(adata, color='sample', components=['1,2'], ax=axs[0, 0], show=False)
sc.pl.tsne(adata, color='sample', components=['1,2'], ax=axs[0, 1], show=False)
sc.pl.umap(adata, color='sample', components=['1,2'], ax=axs[1, 0], show=False)<Axes: title={'center': 'sample'}, xlabel='UMAP1', ylabel='UMAP2'>
Finally, we can compare the PCA, tSNE and UMAP.
Discuss
We have now done Variable gene selection, PCA and UMAP with the settings we selected for you. Test a few different ways of selecting variable genes, number of PCs for UMAP and check how it influences your embedding.
7 Genes of interest
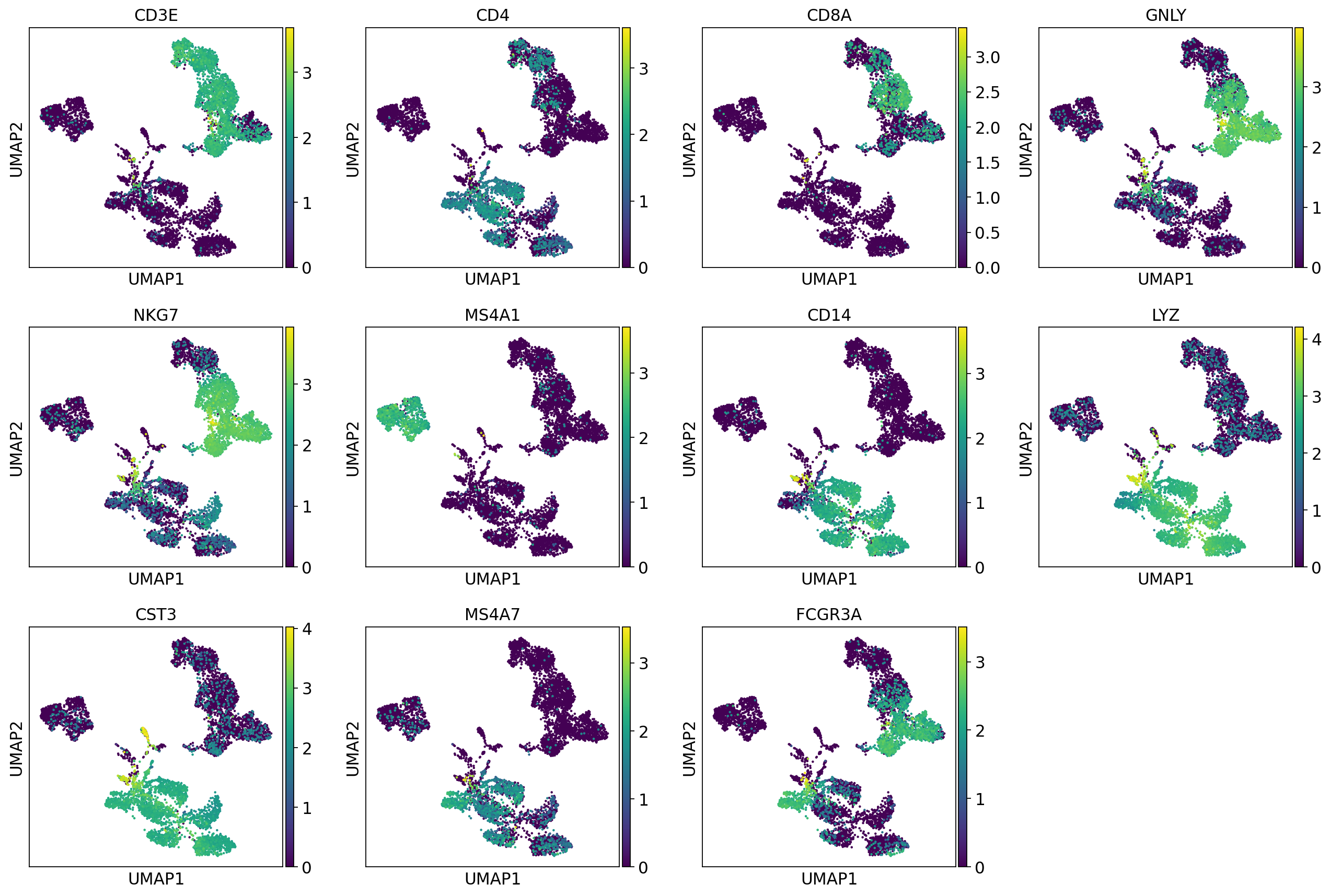
Let’s plot some marker genes for different cell types onto the embedding.
| Markers | Cell Type |
|---|---|
| CD3E | T cells |
| CD3E CD4 | CD4+ T cells |
| CD3E CD8A | CD8+ T cells |
| GNLY, NKG7 | NK cells |
| MS4A1 | B cells |
| CD14, LYZ, CST3, MS4A7 | CD14+ Monocytes |
| FCGR3A, LYZ, CST3, MS4A7 | FCGR3A+ Monocytes |
| FCER1A, CST3 | DCs |
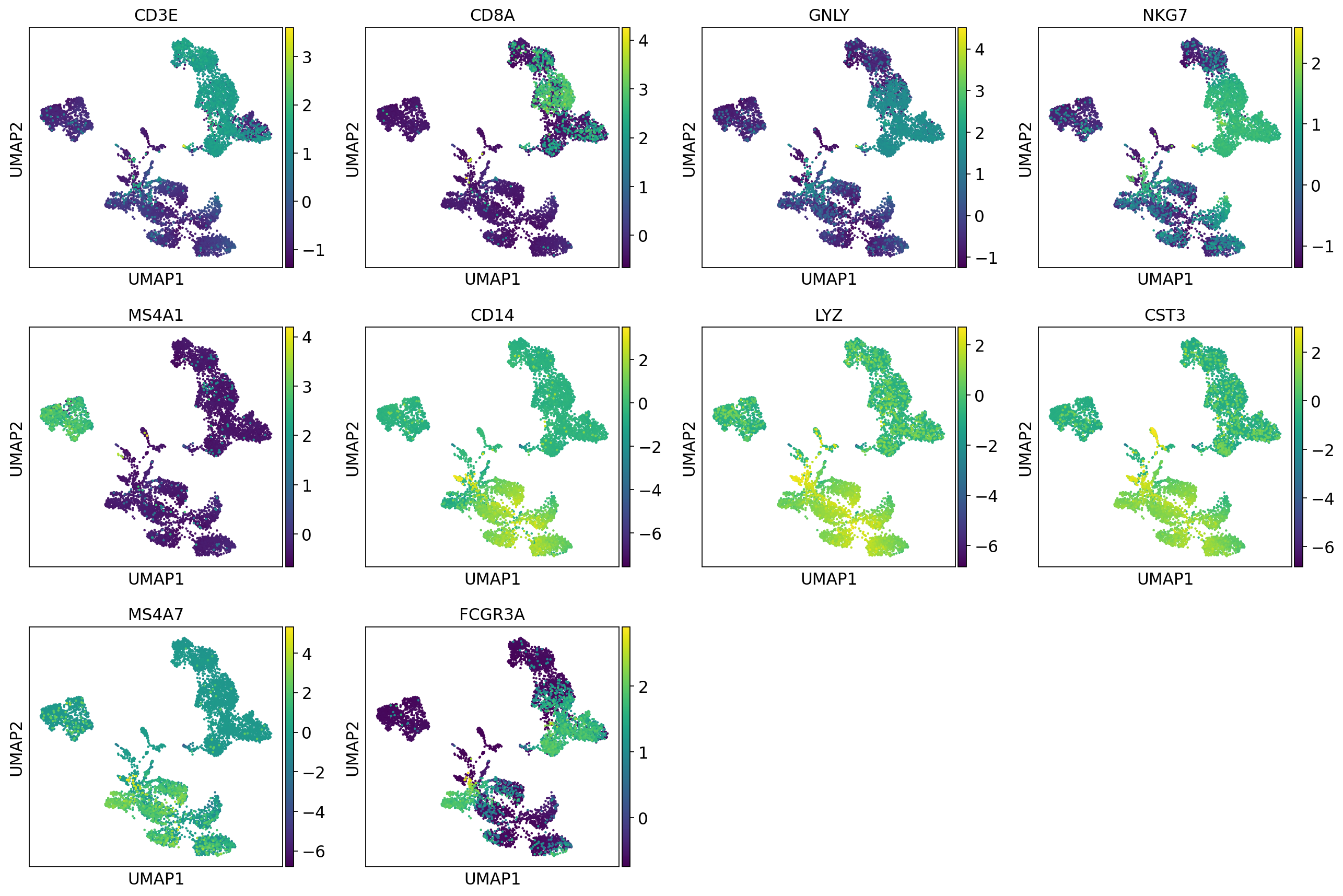
sc.pl.umap(adata, color=["CD3E", "CD4", "CD8A", "GNLY","NKG7", "MS4A1","CD14","LYZ","CST3","MS4A7","FCGR3A"])
The default is to plot gene expression in the normalized and log-transformed data. You can also plot it on the scaled and corrected data by using use_raw=False. However, not all of these genes are included in the variable gene set so we first need to filter them.
genes = ["CD3E", "CD4", "CD8A", "GNLY","NKG7", "MS4A1","CD14","LYZ","CST3","MS4A7","FCGR3A"]
var_genes = adata.var.highly_variable
var_genes.index[var_genes]
varg = [x for x in genes if x in var_genes.index[var_genes]]
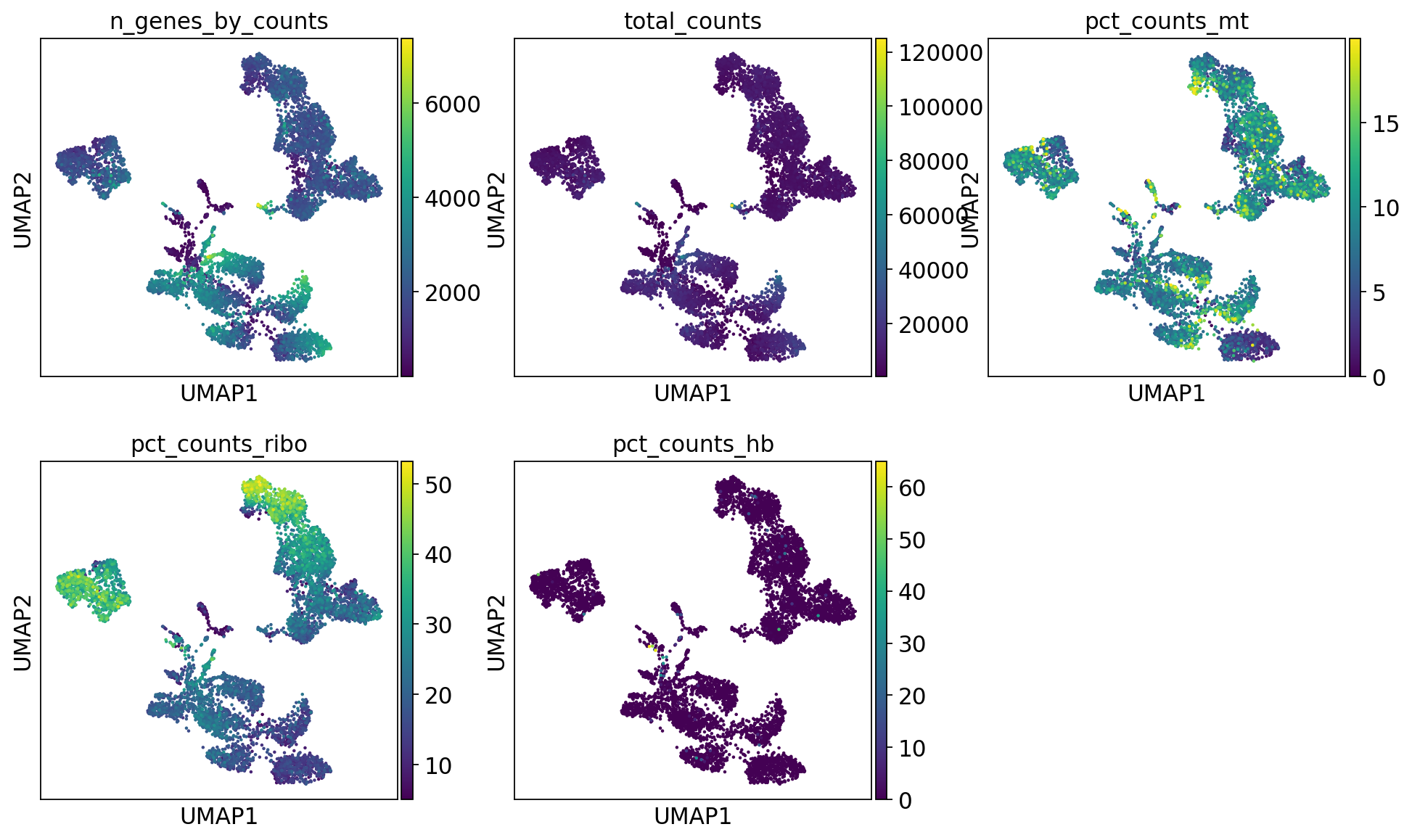
sc.pl.umap(adata, color=varg, use_raw=False)
Discuss
Select some of your dimensionality reductions and plot some of the QC stats that were calculated in the previous lab. Can you see if some of the separation in your data is driven by quality of the cells?
8 Save data
We can finally save the object for use in future steps.
adata.write_h5ad('data/covid/results/scanpy_covid_qc_dr.h5ad')Just a reminder, you need to keep in mind what you have in the X matrix. After these operations you have an X matrix with only variable genes, that are normalized, logtransformed and scaled.
We stored the expression of all genes in raw.X after doing lognormalization so that matrix is a sparse matrix with logtransformed values.
print(adata.X.shape)
print(adata.raw.X.shape)
print(adata.X[:3,:3])
print(adata.raw.X[:10,:10])(7222, 2626)
(7222, 19468)
[[-0.16998859 -0.06050171 -0.08070081]
[-0.19315341 -0.09975121 -0.31379319]
[-0.2051203 -0.11680799 -0.43194618]]
(1, 4) 0.7825693876867097
(8, 7) 1.13110413367469859 Session info
Click here
sc.logging.print_versions()-----
anndata 0.10.5.post1
scanpy 1.9.6
-----
PIL 10.0.0
anyio NA
asttokens NA
attr 23.1.0
babel 2.12.1
backcall 0.2.0
certifi 2023.11.17
cffi 1.15.1
charset_normalizer 3.1.0
colorama 0.4.6
comm 0.1.3
cycler 0.12.1
cython_runtime NA
dateutil 2.8.2
debugpy 1.6.7
decorator 5.1.1
defusedxml 0.7.1
exceptiongroup 1.2.0
executing 1.2.0
fastjsonschema NA
gmpy2 2.1.2
h5py 3.9.0
idna 3.4
igraph 0.10.8
ipykernel 6.23.1
ipython_genutils 0.2.0
jedi 0.18.2
jinja2 3.1.2
joblib 1.3.2
json5 NA
jsonpointer 2.0
jsonschema 4.17.3
jupyter_events 0.6.3
jupyter_server 2.6.0
jupyterlab_server 2.22.1
kiwisolver 1.4.5
leidenalg 0.10.1
llvmlite 0.41.1
louvain 0.8.1
markupsafe 2.1.2
matplotlib 3.8.0
matplotlib_inline 0.1.6
mpl_toolkits NA
mpmath 1.3.0
natsort 8.4.0
nbformat 5.8.0
networkx 3.2.1
numba 0.58.1
numpy 1.26.3
opt_einsum v3.3.0
overrides NA
packaging 23.1
pandas 2.2.0
parso 0.8.3
patsy 0.5.6
pexpect 4.8.0
pickleshare 0.7.5
pkg_resources NA
platformdirs 3.5.1
prometheus_client NA
prompt_toolkit 3.0.38
psutil 5.9.5
ptyprocess 0.7.0
pure_eval 0.2.2
pvectorc NA
pycparser 2.21
pydev_ipython NA
pydevconsole NA
pydevd 2.9.5
pydevd_file_utils NA
pydevd_plugins NA
pydevd_tracing NA
pygments 2.15.1
pynndescent 0.5.11
pyparsing 3.1.1
pyrsistent NA
pythonjsonlogger NA
pytz 2023.3
requests 2.31.0
rfc3339_validator 0.1.4
rfc3986_validator 0.1.1
scipy 1.12.0
send2trash NA
session_info 1.0.0
six 1.16.0
sklearn 1.4.0
sniffio 1.3.0
socks 1.7.1
sparse 0.15.1
stack_data 0.6.2
statsmodels 0.14.1
sympy 1.12
texttable 1.7.0
threadpoolctl 3.2.0
torch 2.0.0
tornado 6.3.2
tqdm 4.65.0
traitlets 5.9.0
typing_extensions NA
umap 0.5.5
urllib3 2.0.2
wcwidth 0.2.6
websocket 1.5.2
yaml 6.0
zmq 25.0.2
zoneinfo NA
zstandard 0.19.0
-----
IPython 8.13.2
jupyter_client 8.2.0
jupyter_core 5.3.0
jupyterlab 4.0.1
notebook 6.5.4
-----
Python 3.10.11 | packaged by conda-forge | (main, May 10 2023, 18:58:44) [GCC 11.3.0]
Linux-5.15.0-92-generic-x86_64-with-glibc2.35
-----
Session information updated at 2024-02-06 00:35