4 Clustering

Clustering is about grouping objects together according to similarity. The objects are grouped into clusters so that objectes within the same cluster are more similar to one another than to objects in other clusters.

Clustering is usually performed based on a set of \(n\) objects, each with \(p\) measurements. A single object \(i\) can thus be described by the vector \({\mathbf x}_i = [x_{i1}, x_{i2}, \dots, x_{ip}]\).

With only \(p=2\) measurements these measurements can easily be plotted and we could illustrate clusters by colors.

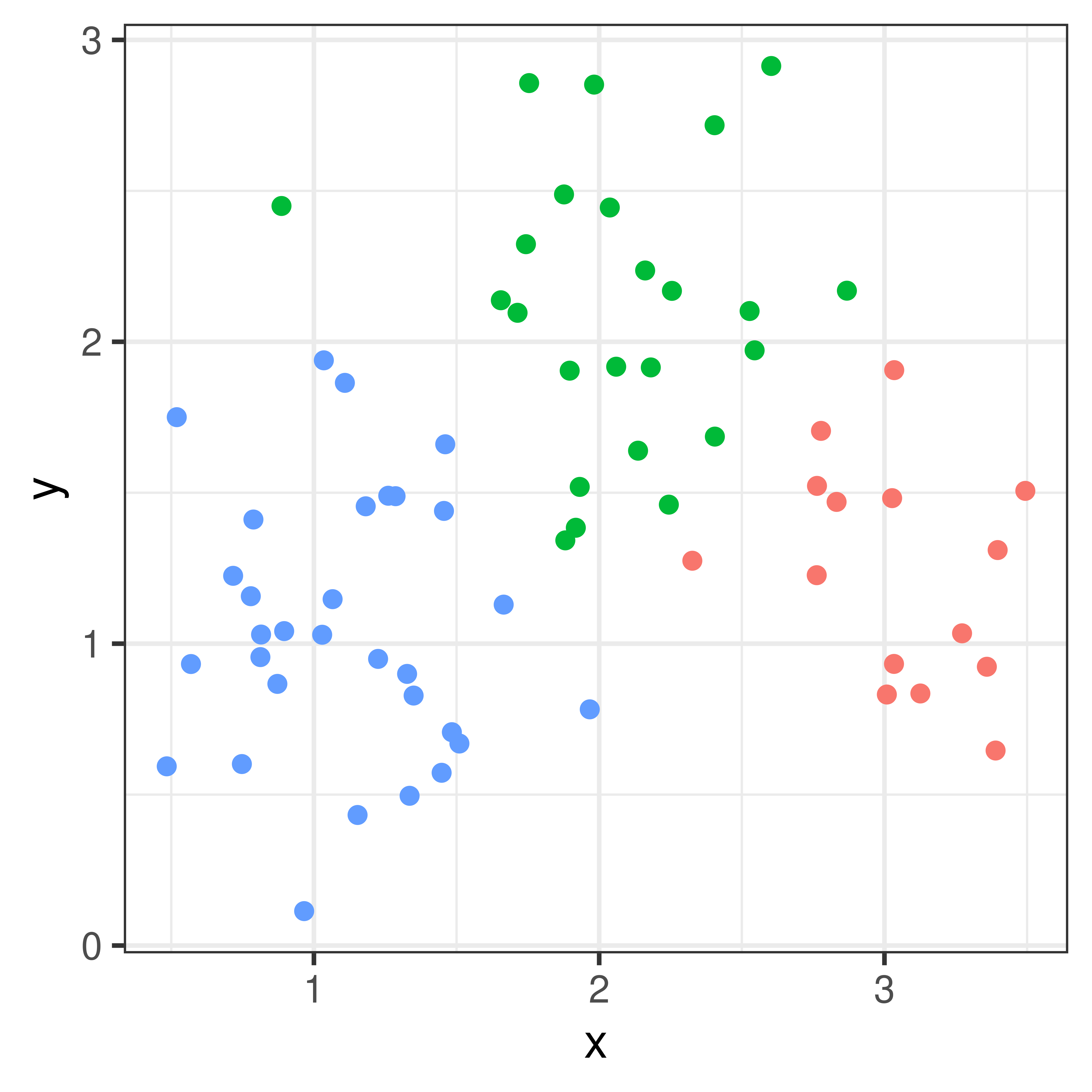
Three clusters

Figure 4.1: Three clusters

Clustering is commonly used for data exploration and to identify substructures in a data set.

There are many types of clustering algorithms, here we will only discuss K-means and hierarchical clustering.

4.1 K-means

The K-means algorith aims to dive all objects into exactly \(K\) clusters. \(K\) has to be given to the algorithm. The K-means algorithm minimize the variance within clusters, by iteratively assigning each object to the cluster with the closest mean (centroid).

The centroid of cluster \(k\) is the arithmetic mean of all \(n_k\) objects in the cluster

\[{\mathbf m}_k = \frac{1}{n_k} \sum_{i=1}^{n_k} {\mathbf x}_{i}\]

The algorithm can be performed as follows;

  1. Initialization. Select \(k\) initial centroids.
  2. Assign each object to the closest centroid (in terms of squared Euclidean distance). The squared Euclidean distance between an object (a data point) and a cluster centroid \(m_k\) is \(d_i = \sum_{j=1}^p (x_{ij} - m_{kj})^2\). By assigning each object to closest centroid the total within cluster sum of squares (WSS) is minimized. \[WSS = \sum_{k=1}^K\sum_{i \in C_k}\sum_{j=1}^p (x_{ij} - m_{kj})^2\]
  3. Update the centroids for each of the \(k\) clusters by computing the centroid for all the objects in each of the clusters.
  4. Repeat 1-2 until convergence

The initial centroids can be selected in several different ways. Two common methods are;

  • Forgy’s method: Select \(K\) data points as initial centroids
  • Randomly assign each data point to one out of \(K\) clusters and compute the centroids for these initial clusters.

4.2 Dissimilarity matrix

All clustering algorithms need a measure of similarity or dissimilarity between objects. As a similarity can be transformed to a dissimilarity, we will here focus on dissimilaities.

Dissimilarities between all pairs of objects can be described in a dissimilarity matrix. Most algorithms are based on symmetric dissimilarities, i.e. when the dissimilarity between a and b is the same as between b and a. Also, most algorithm require non-negative dissimilarities.

K-means uses the squared Euclidean distance as a dissimilarity measure, but there of course other ways to measure the dissimilarity between two objects (data points).

Common dissimilarity measures include;

Euclidean distance \[d_{euc} (x, y) = \sqrt{\sum_{j=1}^{p} (x_j - y_j)^2}\] Squared Euclidean distance \[d_{euc} (x, y) = \sum_{j=1}^{p} (x_j - y_j)^2\]

Manhattan distance \[d_{man} (x, y) = \sqrt{\sum_{j=1}^{p} |x_j - y_j|}\] Pearson correlation distance

Pearson’s correlation is a similarity measure

\[r = \frac{\sum_{j=1}^p(x_j-\bar x)(y_i-\bar y)}{\sqrt{\sum_{j=1}^p(x_j-\bar x)^2\sum_{j=1}^p(y_j-\bar y)^2}}\]

Using a transformation we can compute a Pearson’s correlation distance

\[d_{pear}(x,y) = \sqrt{1-r}\]

4.3 Hierarchical clustering

Hierarchical clustering does not require the number of clusters to be specified. Instead of creating a single set of clusters it creates a hierarchy of clusterings based on pairwise dissimilarities.

A hierarchical cluster dendrogram.

Figure 4.2: A hierarchical cluster dendrogram.

There are two strategies for hierarchical clustering agglomerative (bottom-up) and divisive (top-down).

The agglomerative strategy starts att the bottom with all objects in separate clusters and at each level merge a pair of clusters. The merged pair of clusters are those with the smallest dissimilarity.

The divisive strategy starts at the top with all objects in a single cluster and at each level one cluster is split into two. The split is chosen to produce the two groups with the largest possible dissimilarity.

With \(n\) objects to cluster both strategies will produce a dendrogram representing the \(n-1\) levels in the hierarchy. Each level represent a specific clustering of the objects into disjoint clusters. The heights of the branches in the dendrogram are proportional to the dissimilarity of the merged/split clusters.

4.3.1 Agglomerative clustering

Agglomerative clustering starts with all objects in separate clusters and at each level merge the pair of clusters with the smallest dissimilarity. The pairwise dissilimarities between objects are known, but a method for computing dissimilarity between clusters is needed, as so called linkage method.

The dissimilarity between two clusters A and B with objects \(a_1, \dots, a_{n_A}\) and \(b_1, \dots, b_{n_B}\), respectively, can be computed using one of several linkage methods.

Single linkage

Single linkage takes as a cluster dissimilarity the distance between the two closest objects in the two clusters.

\[d_{sl}(A, B) = \min_{i,j} d(a_i, b_j)\]

Complete linkage

Complete linkage takes as a cluster dissimilarity the distance between the two objects furthest apart in the two clusters.

\[d_{cl}(A, B) = \max_{i,j} d(a_i, b_j)\]

Average linkage

Average linkage takes as a cluster dissimilarity the average distance between the objects in the in the two clusters.

\[d_{al}(A, B) = \frac{1}{n_A n_B}\sum_i\sum_j d(a_i, b_j)\]

Single, complete and average linkage are the most common linkage methods and these can be combined with any pairwise dissimilarity measures.

Ward’s linkage

Ward’s linkage method minimize the within variance, by merging clusters with the minimum increase in within sum of squares.

\[d_{wl}(A, B) = \sum_{i=1}^{n_A} (a_i - m_{A \cup B})^2 + \sum_{i=1}^{n_B} (b_i - m_{A \cup B})^2 - \sum_{i=1}^{n_A} (a_i - m_{A})^2 - \sum_{i=1}^{n_B} (b_i - m_{B})^2\] where \(m_A, m_B, m_{A \cup B}\) are the center of the clusters \(A\), \(B\) and \(A \cup B\), respectively.

Note that Ward’s linkage method should not be combined with any dissimilarity matrix as it is based on the squared Euclidean distance. In the R function hclust either the Euclidean or squared Euclidean distance can be used in combination with the linkage method='ward.D' or method='ward.D2, respectively.

Hierarchical clustering of the same data set using Euclidean distance and four different linkage methods.Hierarchical clustering of the same data set using Euclidean distance and four different linkage methods.Hierarchical clustering of the same data set using Euclidean distance and four different linkage methods.Hierarchical clustering of the same data set using Euclidean distance and four different linkage methods.

Figure 4.3: Hierarchical clustering of the same data set using Euclidean distance and four different linkage methods.

Exercises: Clustering

Exercise 4.1 Based on a two dimensional data set you will investigate K-means clustering.

Download the two-dimensional data set.

  1. Try to cluster the data using the k-means algorithm (function kmeans in R). Use Forgy’s method for initialization and select a value for \(k\). If you get a message that the algorithm did not converge in 10 iterations, try increasing the number of iterations
  2. Plot the data and color by cluster id
  3. Run the same analysis again, do you get the same results? (You can compare two vectors of class identities using the function table.)
  4. By setting the argument nstart to 4 the algorithm will automatically try four different (random) starting points.
  5. Try different values for \(k\), run the k-means algorithm and collect the WSS (‘tot.withinss’). Plot WSS vs k. Thw WSS is always decreasing as k increases, but the curve can still give you a hint of which \(k\) to choose. The Elbow method for selecting \(k\) is to look at this curve and choose the \(k\) that you find at the bend of the curve, at the ‘elbow’. Which \(k\) would you pick based on this?

Exercise 4.2 The NCI60 data set consists of gene expression values for 6830 genes for 64 cell lines.

Using this data set investigate a few hierarchical clustering distances and linkage methods.

The data can be downloaded in R using the following command

  • What is the size of the data matrix? Do every column represent a gene or a cell line?
  • Compute the Euclidean distance between cell lines. This can be accomplished using the function dist. Read the help text ?dist. This function computes the distance between rows of the input data matrix. If the rows represent cell lines, you can run dist(nci.data), but if your cell lines are represented by columns you need to transpose the data matrix first dist(t(nci.data)).
  • Cluster the cell lines using complete linkage hierarchical clustering, use the function hclust.
  • Plot the result! (If you read the help text about hclust you should know how to plot)
    • Try changing the labels to something more informative (such as label=nci.label).
    • Investigate the argument hang, what happens if you set it to -1?
  • Try the linkage methods “single”, “average” and “ward.D” in addition to “complete”. Compare the results. Which method do you think is ‘best’?
  • Pick the tree resulting from the method you think is ‘best’. How many clusters are there? You can cut the tree on any level to get between 1 and 64 clusters. The function cutree cuts either on a specific height (dissimilarity) or to get a specific number of clusters.
  • Compute the Pearson correlation between the cell lines, use the function cor
  • Convert the correlation matrix to a dissimilarity matrix and cluster using complete or average linkage.

4.3.2 Solutions

4.1

## Warning: did not converge in 10 iterations

## Warning: did not converge in 10 iterations

## Warning: did not converge in 10 iterations

## Warning: did not converge in 20 iterations

4.2

## [1] 6830   64