2  Wilcoxon signed rank test I

for a median

Code 
# load libraries
library(tidyverse)
library(magrittr)
library(kableExtra)

Named after Frank Wilcoxon (1892–1945), Wilcoxon signed rank test was one of the first “non-parametric” methods developed. It can be used to:

  1. compare the sample median against a hypothetical median (equivalent to one sample t-test)
  2. examine the difference between paired observations (equivalent to paired t-test). It does make some assumptions about the data, namely:

Example 2.1 (Wilcoxon signed rank test (for a median)) Let’s imagine we are a part of team analyzing results of a placebo-controlled clinical trial to test the effectiveness of a sleeping drug. We have collected data on 10 patients when they took a sleeping drug and when they took a placebo.

The hours of sleep recorded for each study participant:

Code 
# input data
data.sleep <- data.frame(id = 1:10, 
                         drug = c(6.1, 6.0, 8.2, 7.6, 6.5, 5.4, 6.9, 6.7, 7.4, 5.8), 
                         placebo = c(5.2, 7.9, 3.9, 4.7, 5.3, 7.4, 4.2, 6.1, 3.8, 7.3)) 

print(data.sleep)
   id drug placebo
1   1  6.1     5.2
2   2  6.0     7.9
3   3  8.2     3.9
4   4  7.6     4.7
5   5  6.5     5.3
6   6  5.4     7.4
7   7  6.9     4.2
8   8  6.7     6.1
9   9  7.4     3.8
10 10  5.8     7.3

Before we investigate the effect of drug, a senior statistician ask us:

“Is the median sleeping time without taking the drug significantly less than the recommended 7 h of sleep?”

2.1 Define the null and alternative hypothesis under study

\(H_0: m = m_0\) the median sleeping time is equal to \(m_0\), \(m_0 = 7\) h

\(H_1 < m_0\) the median sleeping time is less than \(m_0\), \(m_0 = 7\) h

2.2 Calculate the value of the test statistics

  1. we subtract the median from each measurement, \(X_i - m_0\)
  2. we find absolute value of the difference, \(|X_i - m_0|\)
  3. we rank the absolute value of the difference
  4. we find the value of \(W\), the Wilcoxon signed-rank test statistics as \[W =\displaystyle \sum_{i=1}^{n}Z_iR_i \tag{2.1}\] where \(Z_i\) is an indicator variable such as:

\[\begin{equation} Z_i = \left\{ \begin{array}{cc} 0 & \mathrm{if\ } X_i - m_0 < 0 \\ 1 & otherwise \\ \end{array} \right. \end{equation}\]

Code 
m0 <- 7
data.wilcoxon <- data.sleep %>% 
  select(!drug) %>% # remove drug data for now
  rename(x = placebo) %>% # rename placebo column to x so it is easier to type and follow eq
  mutate(`x-m0` = x - 7) %>% # subtract m0
  mutate(`abs(x-m0)` = abs(`x-m0`)) %>% # take absolute value
  mutate(R = rank(`abs(x-m0)`)) %>% # rank
  mutate(Z = ifelse(`x-m0` < 0, 0, 1)) %>% # define indicator variable Z
  mutate(ZR = R*Z) # calculate ranks R times Z

# print the table
data.wilcoxon %>%
  kable() %>% kable_styling(full_width = FALSE)
id x x-m0 abs(x-m0) R Z ZR
1 5.2 -1.8 1.8 6.0 0 0.0
2 7.9 0.9 0.9 3.5 1 3.5
3 3.9 -3.1 3.1 9.0 0 0.0
4 4.7 -2.3 2.3 7.0 0 0.0
5 5.3 -1.7 1.7 5.0 0 0.0
6 7.4 0.4 0.4 2.0 1 2.0
7 4.2 -2.8 2.8 8.0 0 0.0
8 6.1 -0.9 0.9 3.5 0 0.0
9 3.8 -3.2 3.2 10.0 0 0.0
10 7.3 0.3 0.3 1.0 1 1.0
Table 2.1: Demonstrating steps in the calculating W, Wilcoxon signed-rank test statistics on the placebo column: x stands for placebo sleeping hours

We can now calculate \(W\) following equation Equation 2.1 and we get:

Code 
# sum up the ranks multiplied by Z indicator value
W <- data.wilcoxon$ZR %>% sum()
print(W)
[1] 6.5

2.3 Compare the value to the test statistics to values from known probability distribution

We got \(W = 6.5\) and now we need to calculate the P-value associated with \(W\) to be able to make decision about rejecting the null hypothesis. We refer to a statistical table “Upper and Lower Percentiles of the Wilcoxon Signed Rank Test, W” that can be found online or here.

For sample size \(n=10\) we can see that probability of observing \(W \le 3\) or \(W \ge 52\) is small, 0.005. Probability of observing \(W \le 4\) or \(W \ge 51\) is 0.007, still small but slightly larger. While we are getting towards the middle of the distribution the probability of observing \(W\) is getting larger and the probability of observing \(W \le11\) or \(W \ge 44\) is 0.053.

The P-value associated with observing \(W=6.5\) is just under \(0.019\). Assuming 5% significance level, we have enough evidence to reject the null hypothesis and conclude that the median is significantly less than 7 hours.

2.4 Obtaining probablity mass function

Where is the statistical table coming from?

Briefly, Wilcoxon described and showed examples how to calculate both the test statistics \(W\) for an example data as well as the distribution of \(W\) under the null hypothesis Wilcoxon (1945). We can try to find the distribution of W ourselves for a simple scenario with less, four observation (\(n=4\))

Code 
# enumerate all rank possibilties (by hand)
r1 <- c(1, -1, 1, 1, 1, -1, -1, -1, 1, 1, 1, -1, -1, -1, 1, -1)
r2 <- c(2, 2, -2, 2, 2, -2, 2, 2, -2, 2, -2, -2, -2, 2, -2, -2)
r3 <- c(3, 3, 3, -3, 3, 3, -3, 3, -3, -3, 3, -3, 3, -3, -3, -3)
r4 <- c(4, 4, 4, 4, -4, 4, 4, -4, 4, -4, -4, 4, -4, -4, -4, -4)

data.w <- rbind(r1, r2, r3, r4)
data.w.ind <- data.w
data.w.ind[data.w < 0] <- 0
r.sum <- apply(data.w.ind, 2, sum)

data.w <- rbind(data.w, r.sum)
rownames(data.w) <- c("id1", "id4", "id3", "id4", "W")
colnames(data.w) <- paste("c", 1:16, sep="")

data.w %>% kable() %>% kable_styling(full_width = TRUE) %>%
  row_spec(5, bold = T, color = "black", background = "#deebf7")
c1 c2 c3 c4 c5 c6 c7 c8 c9 c10 c11 c12 c13 c14 c15 c16
id1 1 -1 1 1 1 -1 -1 -1 1 1 1 -1 -1 -1 1 -1
id4 2 2 -2 2 2 -2 2 2 -2 2 -2 -2 -2 2 -2 -2
id3 3 3 3 -3 3 3 -3 3 -3 -3 3 -3 3 -3 -3 -3
id4 4 4 4 4 -4 4 4 -4 4 -4 -4 4 -4 -4 -4 -4
W 10 9 8 7 6 7 6 5 5 3 4 4 3 2 1 0
Table 2.2: Enumeration of possible of ranks given 4 observations together with calculated W statistics
  • Given 4 observations, we could get ranks \(R_i\) of 1, 2, 3 or 4 only
  • Further, depending where the observation would be with respect to \(m_0\), the rank \(R_i\) could be positive or negative.
  • For example, the first column \(c1\) corresponds to all 4 observations having positive ranks, so all \(x_i - m_0 > 0\), whereas column \(c16\) corresponds to all observations having negative ranks, so \(x_i - m_0 < 0\).
  • As \(W\) test statistics is derived by summing up the positive ranks, we can see by listing all the combinations in the table, that \(0 \le W \le10\).

We can also now write down the probability mass function given the table.

Code 
# calculate probability mass function
W <- data.w[5,]

df.w <- data.frame(W = W) %>%
  group_by(W) %>%
  summarize(n = n()) %>%
  mutate(per = n / 16) 

dist.W <- rbind(W = formatC(df.w$W), `p(W)`=df.w$per)

dist.W %>% t() %>%
  kable(digits = 2) %>%
  kable_styling(full_width = T) %>%
  row_spec(1, )
W p(W)
0 0.0625
1 0.0625
2 0.0625
3 0.125
4 0.125
5 0.125
6 0.125
7 0.125
8 0.0625
9 0.0625
10 0.0625
Table 2.3: Probability mass function for 4 observations
Code 
# plot pmf
barplot(df.w$per, names.arg = 0:10, ylab = "p(W)", xlab="W")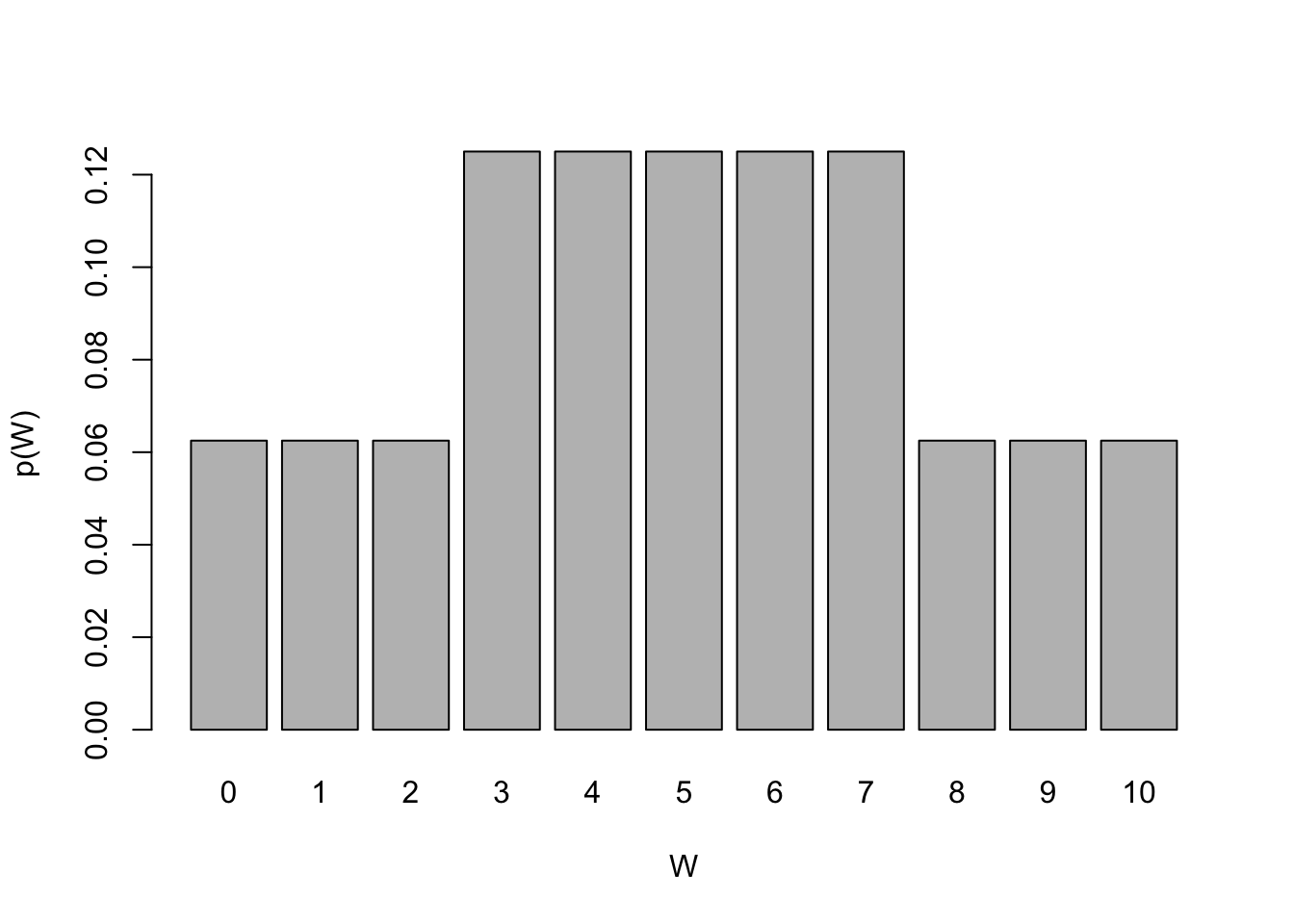

Figure 2.1: Probablity mass function for observations

Now we can use our knowledge from the Probability session on discrete distributions to calculate the probability associated with observing test statistics \(W\) given the known probability mass function.

For more examples on how to manually obtain the distribution \(W\) under the null hypothesis visit PennState Elbery collage website.

2.5 In R we use wilcox.test() function:

# run Wilcoxon signed rank test for a median
wilcox.test(x = data.sleep$placebo, 
            y = NULL,
            alternative = "less",
            mu = 7, 
            exact = F
            )

    Wilcoxon signed rank test with continuity correction

data:  data.sleep$placebo
V = 6.5, p-value = 0.01827
alternative hypothesis: true location is less than 7