Mathematical statistics and machine learning in R
RaukR 2024 • Advanced R for Bioinformatics
Nikolay Oskolkov
21-Jun-2024
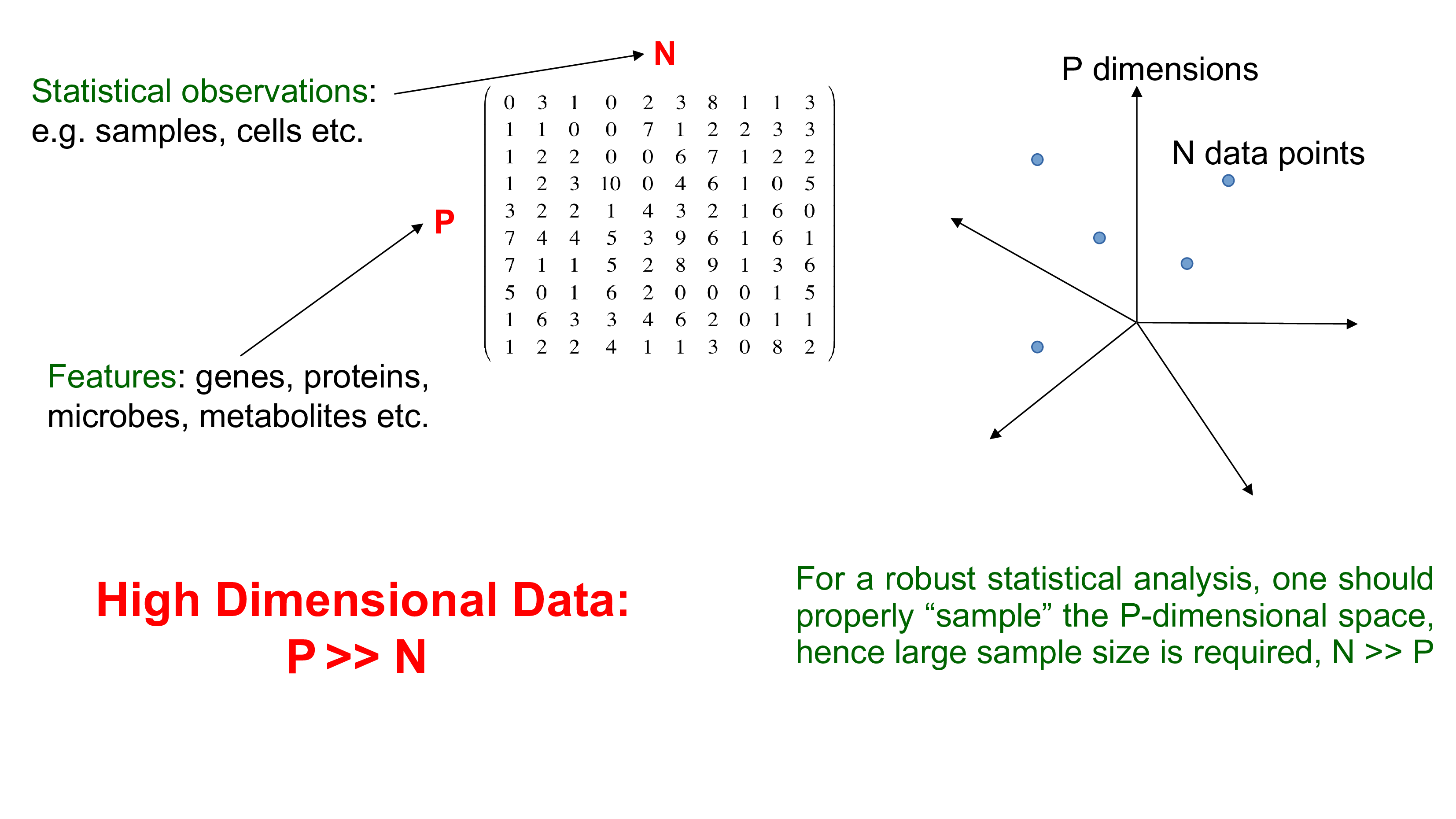
Biological data are high dimensional
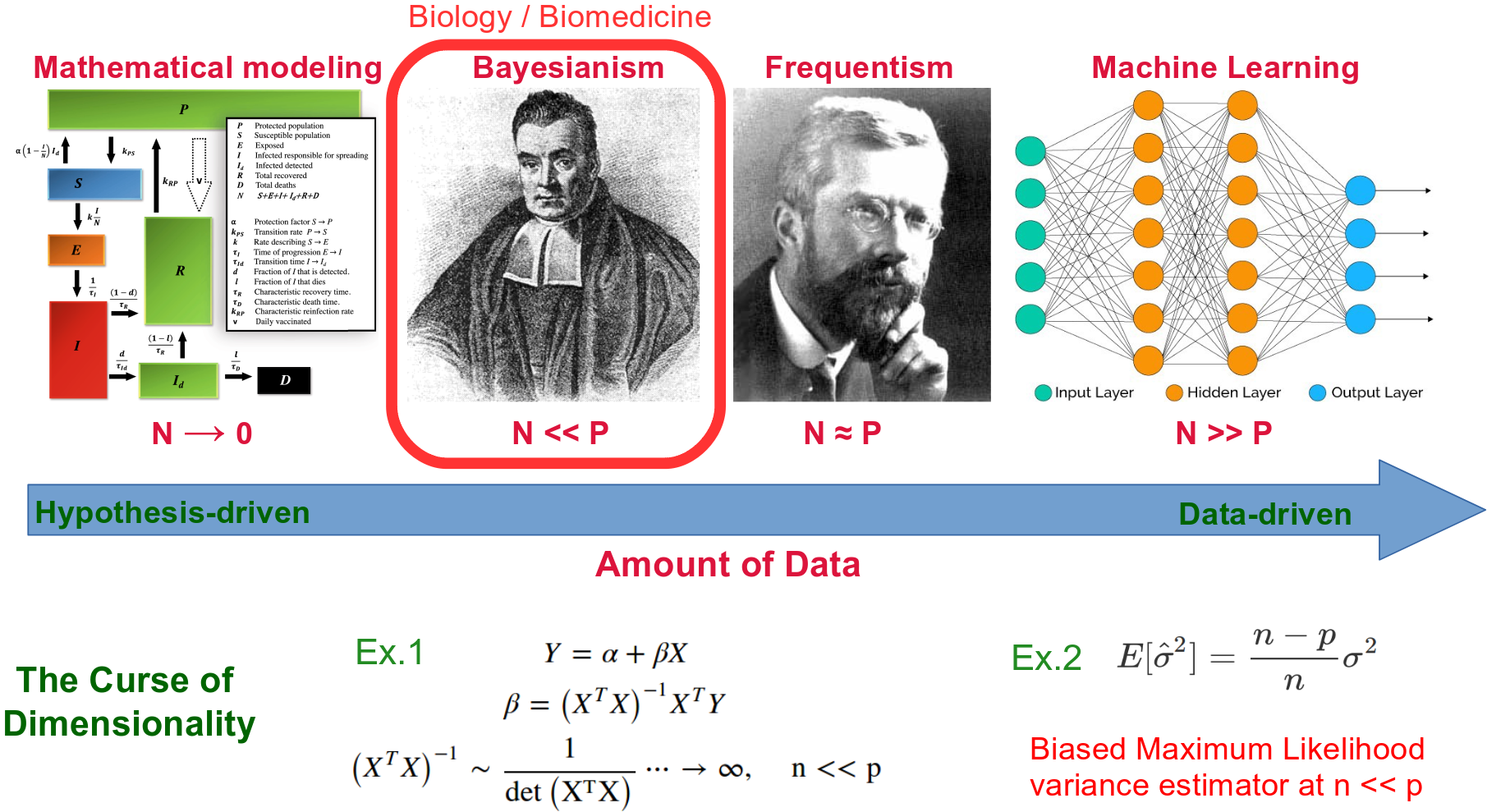
Types of data analysis
Some peculiarities of Frequentist statistics
- based on Maximum Likelihood principle
- focus
too muchon summary statistics
\[\rm{L}\,(\,x_i \,|\, \mu,\sigma^2\,) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp^{\displaystyle -\frac{\sum\limits_{i=1}^N (x_i-\mu)^2}{2\sigma^2}}\]
\[\frac{\partial \rm{L}\,(\,x_i \,|\, \mu,\sigma^2\,)}{\partial\mu} = 0; \,\, \frac{\partial \rm{L}\,(\,x_i \,|\, \mu,\sigma^2\,)}{\partial\sigma^2} = 0\]
\[\mu = \frac{1}{N}\sum_{i=0}^N x_i \,\,\rm{-}\,\rm{mean \, estimator}\]
\[\sigma^2 = \frac{1}{N}\sum_{i=0}^N (x_i-\mu)^2 \,\,\rm{-}\,\rm{variance \, estimator}\]
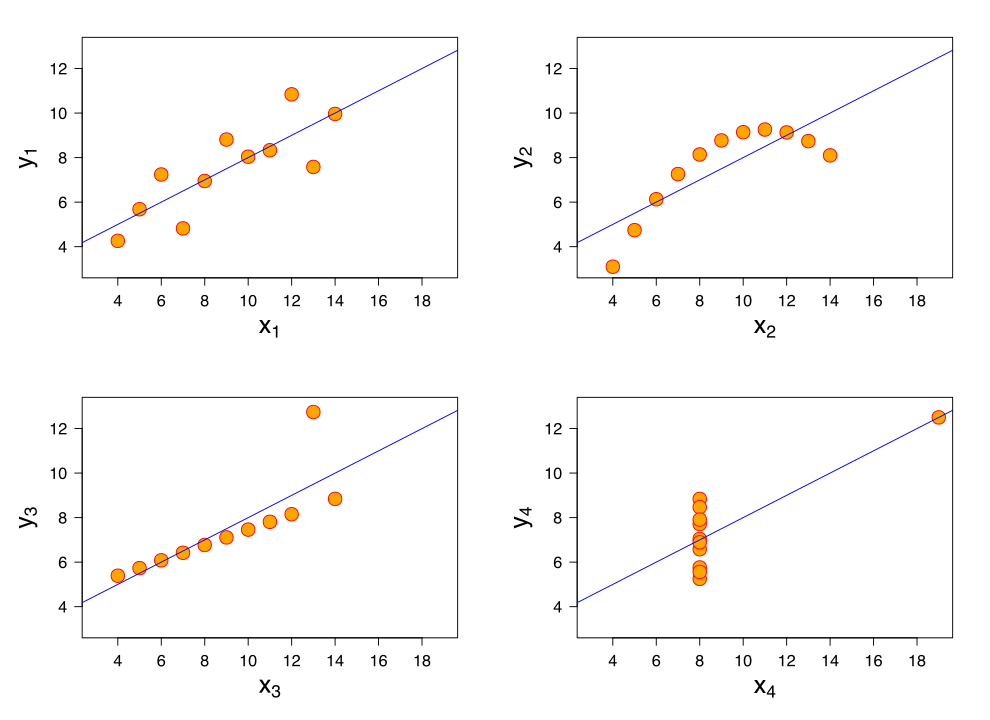 Summary statistics do not always reasonbly describe data (example: Anscombes quartet)
Summary statistics do not always reasonbly describe data (example: Anscombes quartet)
Frequentist statistics: focus to much on p-values
FC<-1.02; x_mean<-5; x_sd<-1; N_vector<-seq(from=100,to=10000,by=100); pvalue_t<-vector(); pvalue_lm<-vector()
for(N in N_vector)
{
x1 <- rnorm(N, x_mean, x_sd); x2 <- rnorm(N, x_mean*FC, x_sd)
t_test_res<-t.test(x1, x2); pvalue_t <- append(pvalue_t, t_test_res$p.value)
x <- rnorm(N, 0, 1); y <- 0.1*x+2*rnorm(N, 0, 1)
lm_res <- summary(lm(y~x)); pvalue_lm <- append(pvalue_lm, lm_res$coefficients[2,4])
}
par(mfrow=c(2,2)); par(mar = c(5, 5, 1, 1))
boxplot(x1, x2, names=c("X1","X2"), ylab="Value", col="darkred"); mtext("Fold change FC = 1.02")
plot(pvalue_t~N_vector,type='o',xlab="N",ylab="p-value",col="darkgreen"); mtext("P-value of two-group t-test")
plot(y~x, xlab="X", ylab="Y"); abline(lm(y~x), col="blue", lwd=2); mtext("Y = 0.1*X + 2*rnorm(N, 0, 1)")
plot(pvalue_lm~N_vector,type='o',xlab="N",ylab="p-value",col="darkgreen"); mtext("P-value of linear regression")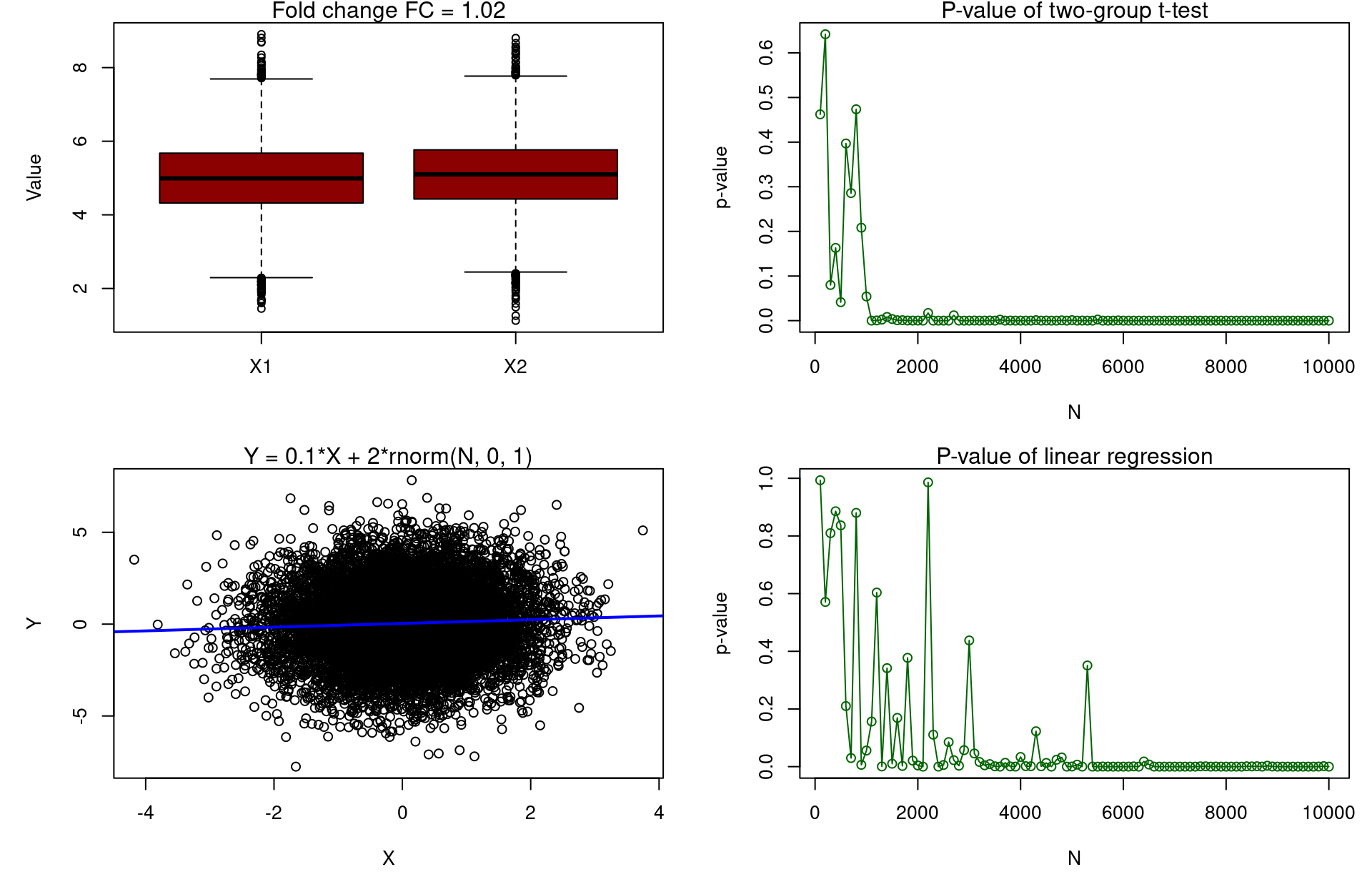

Questionable whether p-value is a best metric for ranking features (biomarkers)
Frequentist statistics struggles with high-dimensional data
n <- 20 # number of samples
p <- 2 # number of features / dimensions
Y <- rnorm(n)
X <- matrix(rnorm(n * p), n, p)
summary(lm(Y ~ X))
Call:
lm(formula = Y ~ X)
Residuals:
Min 1Q Median 3Q Max
-2.0522 -0.6380 0.1451 0.3911 1.8829
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.14950 0.22949 0.651 0.523
X1 -0.09405 0.28245 -0.333 0.743
X2 -0.11919 0.24486 -0.487 0.633
Residual standard error: 1.017 on 17 degrees of freedom
Multiple R-squared: 0.02204, Adjusted R-squared: -0.09301
F-statistic: 0.1916 on 2 and 17 DF, p-value: 0.8274Going to higher dimensions →
n <- 20 # number of samples
p <- 10 # number of features / dimensions
Y <- rnorm(n)
X <- matrix(rnorm(n * p), n, p)
summary(lm(Y ~ X))
Call:
lm(formula = Y ~ X)
Residuals:
Min 1Q Median 3Q Max
-1.0255 -0.4320 0.1056 0.4493 1.0617
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.54916 0.26472 2.075 0.0679 .
X1 0.30013 0.21690 1.384 0.1998
X2 0.68053 0.27693 2.457 0.0363 *
X3 -0.10675 0.26010 -0.410 0.6911
X4 -0.21367 0.33690 -0.634 0.5417
X5 -0.19123 0.31881 -0.600 0.5634
X6 0.81074 0.25221 3.214 0.0106 *
X7 0.09634 0.24143 0.399 0.6992
X8 -0.29864 0.19004 -1.571 0.1505
X9 -0.78175 0.35408 -2.208 0.0546 .
X10 0.83736 0.36936 2.267 0.0496 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.8692 on 9 degrees of freedom
Multiple R-squared: 0.6592, Adjusted R-squared: 0.2805
F-statistic: 1.741 on 10 and 9 DF, p-value: 0.2089Going to even higher dimensions →
n <- 20 # number of samples
p <- 20 # number of features / dimensions
Y <- rnorm(n)
X <- matrix(rnorm(n * p), n, p)
summary(lm(Y ~ X))
Call:
lm(formula = Y ~ X)
Residuals:
ALL 20 residuals are 0: no residual degrees of freedom!
Coefficients: (1 not defined because of singularities)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.34889 NaN NaN NaN
X1 0.66218 NaN NaN NaN
X2 0.76212 NaN NaN NaN
X3 -1.35033 NaN NaN NaN
X4 -0.57487 NaN NaN NaN
X5 0.02142 NaN NaN NaN
X6 0.40290 NaN NaN NaN
X7 0.03313 NaN NaN NaN
X8 -0.31983 NaN NaN NaN
X9 -0.92833 NaN NaN NaN
X10 0.18091 NaN NaN NaN
X11 -1.37618 NaN NaN NaN
X12 2.11438 NaN NaN NaN
X13 -1.75103 NaN NaN NaN
X14 -1.55073 NaN NaN NaN
X15 0.01112 NaN NaN NaN
X16 -0.50943 NaN NaN NaN
X17 -0.47576 NaN NaN NaN
X18 0.31793 NaN NaN NaN
X19 1.43615 NaN NaN NaN
X20 NA NA NA NA
Residual standard error: NaN on 0 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: NaN
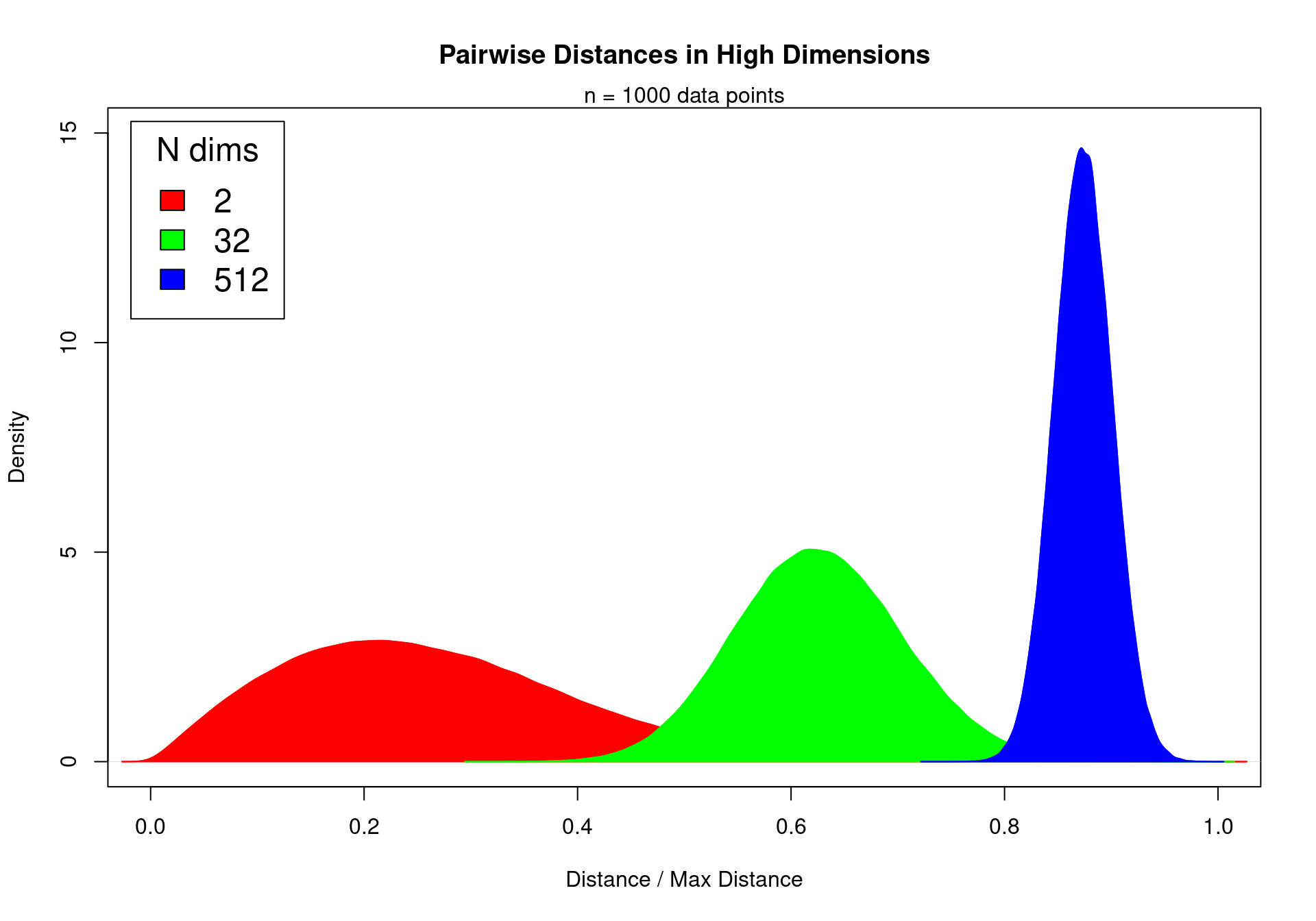
F-statistic: NaN on 19 and 0 DF, p-value: NAEquidistant points in high dimensions
Data points in high dimensions:
move away from each other
become equidistant and similar
Impossible to see differences between cases and controls
Regularizations: LASSO
\[Y = \beta_1X_1+\beta_2X_2+\epsilon\]
\[\textrm{OLS} = (Y-\beta_1X_1-\beta_2X_2)^2\]
\[\textrm{Penalized OLS} = (Y-\beta_1X_1-\beta_2X_2)^2 + \lambda(|\beta_1|+|\beta_2|)\]
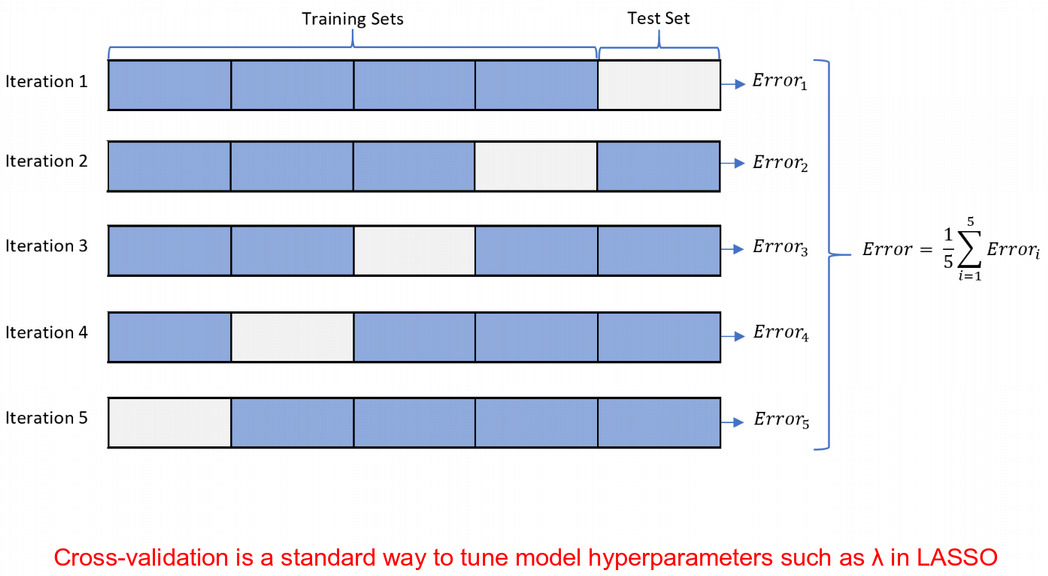
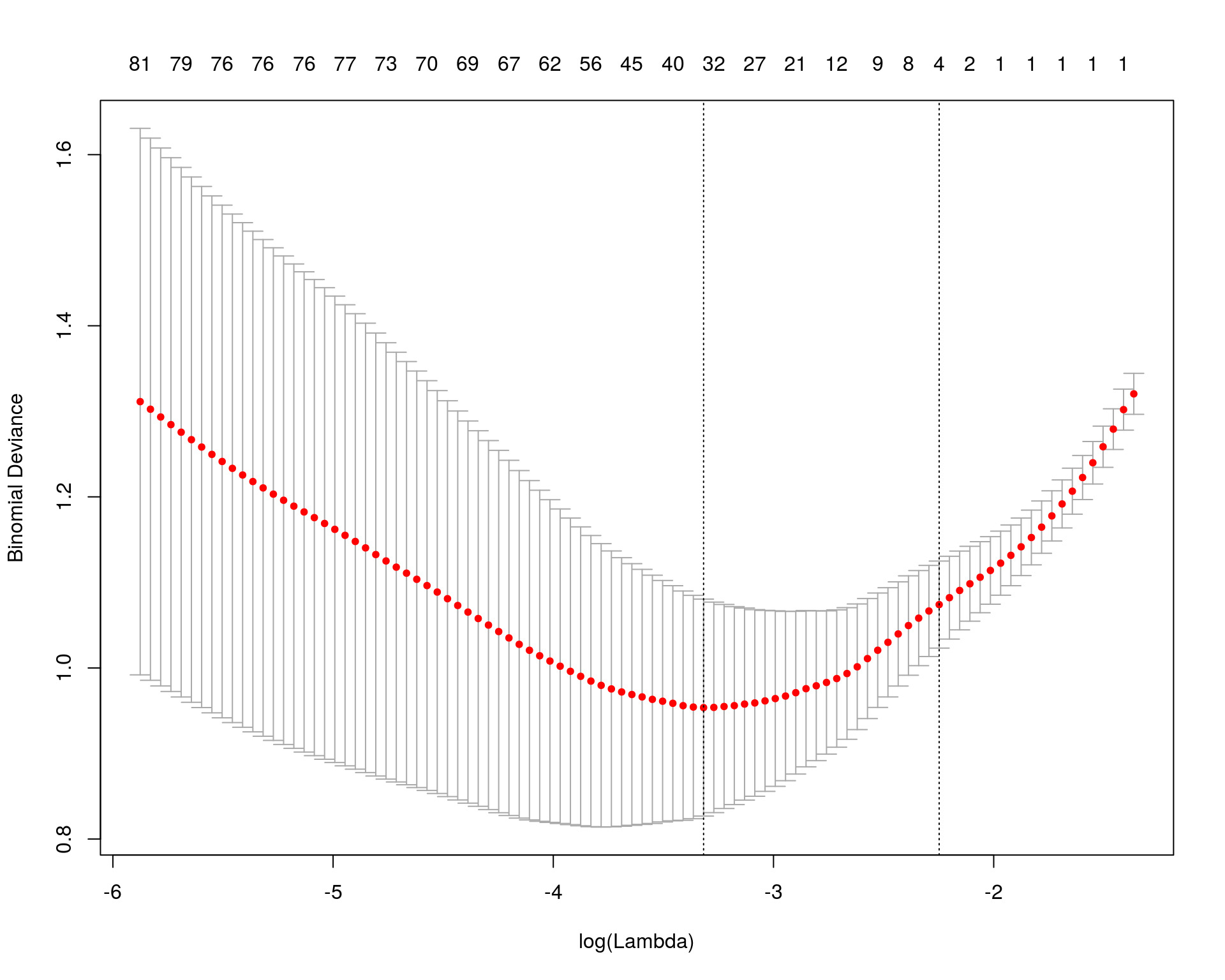
Regularizations are priors in Bayesian statistics
\[\small Y = \beta_1X_1+\beta_2X_2+\epsilon; \,\,\, Y \sim N(\,\beta_1X_1+\beta_2X_2, \sigma^2\,) \equiv \rm{L}\,(\,\rm{Y} \,|\, \beta_1,\beta_2\,)\]
- Maximum Likelihood principle: maximize probability to observe data given parameters: \[\small \rm{L}\,(\,\rm{Y} \,|\, \beta_1,\beta_2\,) = \frac{1}{\sqrt{2\pi\sigma²}} \exp^{\displaystyle -\frac{(Y-\beta_1X_1-\beta_2X_2)^2}{2\sigma²}}\]
- Bayes theorem: maximize posterior probability of observing parameters given data: \[\small \rm{Posterior}(\rm{params} \,|\, \rm{data})=\frac{L(\rm{data} \,|\, \rm{params})*\rm{Prior}(\rm{params})}{\int{L(\rm{data} \,|\, \rm{params})*\rm{Prior}(\rm{params}) \, d(\rm{params})}}\]
\[\small \rm{Posterior}(\,\beta_1,\beta_2\,|\, \rm{Y}\,) \sim \rm{L}\,(\,\rm{Y} \,|\,\beta_1,\beta_2\,)*\rm{Prior}(\beta_1,\beta_2) \sim \exp^{-\frac{(Y-\beta_1X_1-\beta_2X_2)^2}{2\sigma²}}*\exp^{-\lambda(|\beta_1|+|\beta_2|)} \\ \small -\log{\left[\rm{Posterior}(\, \beta_1,\beta_2 \,|\, \rm{Y}\,)\right]} \sim (Y-\beta_1X_1-\beta_2X_2)^2 + \lambda(|\beta_1|+|\beta_2|)\]
Markov Chain Monte Carlo (MCMC): introduction
- Integration via Monte Carlo sampling
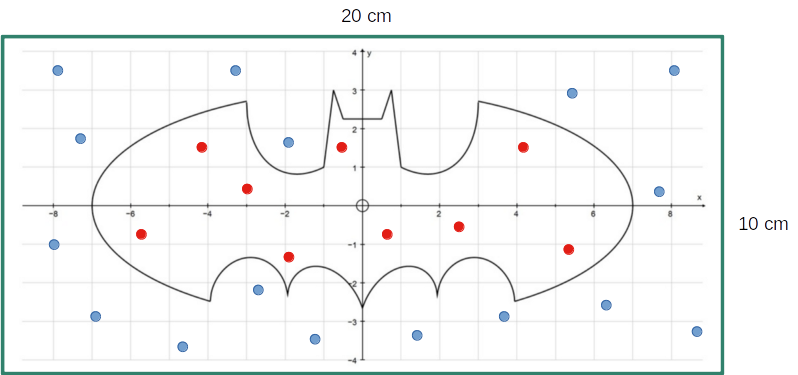
\[\small I = 2\int\limits_2^4{x dx}=2\frac{x^2}{2} \Big|_2^4 = 16 - 4 = 12\]
f <- function(x){return(2*x)}; a <- 2; b <- 4; N <- 10000; count <- 0
x <- seq(from = a, to = b, by = (b-a) / N); y_max <- max(f(x))
for(i in 1:N)
{
x_sample <- runif(1, a, b); y_sample <- runif(1, 0, y_max)
if(y_sample <= f(x_sample)){count <- count + 1}
}
paste0("Integral by Monte Carlo: I = ", (count / N) * (b - a) * y_max)[1] "Integral by Monte Carlo: I = 11.9248"- Markov Chain Monte Carlo (MCMC)
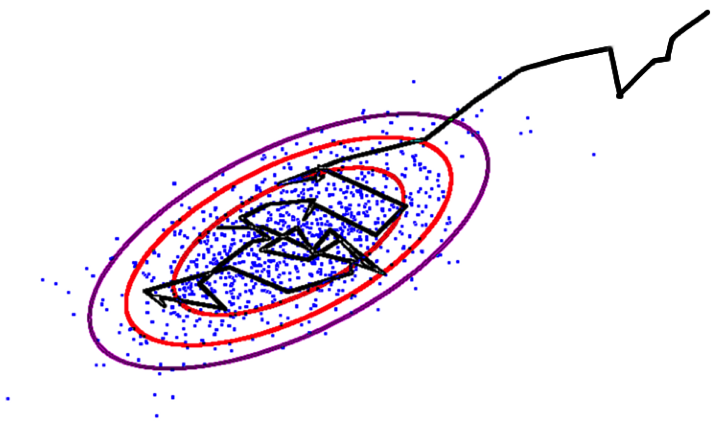
\[\small \rm{Hastings \,\, ratio} = \frac{\rm{Posterior}\,(\,\rm{params_{next}} \,|\, \rm{data}\,)}{\rm{Posterior}\,(\,\rm{params_{previous}} \,|\, \rm{data}\,)}\]
- If Hastings ratio > u [0, 1], then accept, else reject
- Hastings ratio does not contain the intractable integral from Bayes theorem
Markov Chain Monte Carlo (MCMC) from scratch in R
- Example from population genetics
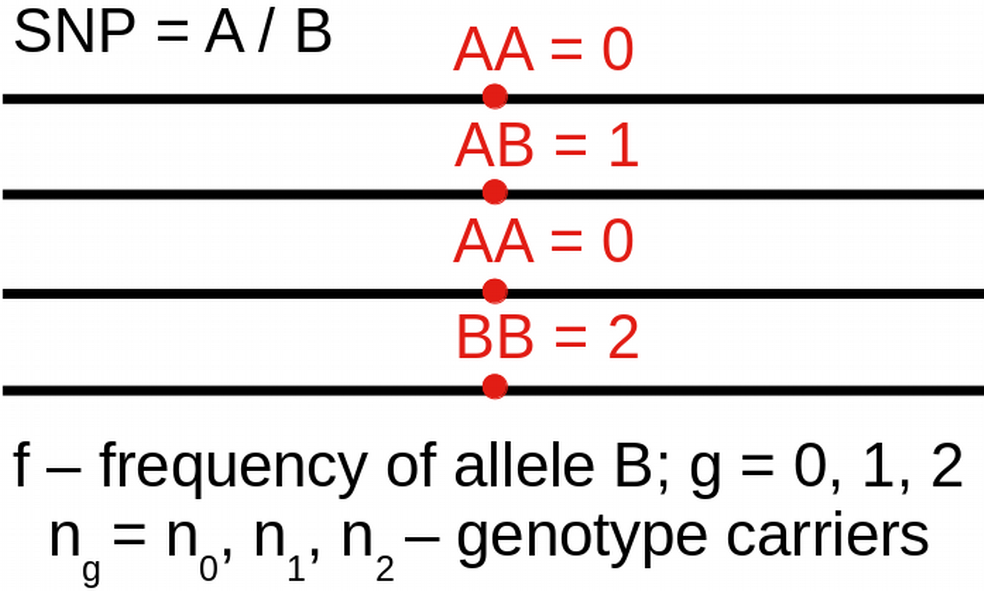
\[\small L(n \, | \, f) = \prod_g{\left[ {2\choose g} f^g (1-f)^{2-g} \right]^{n_g}}\]
\[\small \frac{\partial \log\left[L(n | f)\right]}{\partial f} = 0 \, \Rightarrow \hat{f}=\frac{n_1+2n_2}{2(n_0+n_1+n_2)}\]
\[\small \rm{Prior}(f, \alpha, \beta) = \frac{1}{B(\alpha, \beta)} f^{\alpha-1} (1-f)^{\beta-1}\]
N <- 100; n <- c(25, 50, 25) # Observed genotype data for N individuals
f_MLE <- (n[2] + 2*n[3]) / (2 * sum(n)) # MLE of allele frequency
# Define log-likelihood function (log-binomial distribution)
LL <- function(n, f){return((n[2] + 2*n[3])*log(f) + (n[2] + 2*n[1])*log(1-f))}
# Define log-prior function (log-beta distribution)
LP <- function(f, alpha, beta){return(dbeta(f, alpha, beta, log = TRUE))}
# Run MCMC Metropolis - Hastings sampler
f_poster <- vector(); alpha <- 0.5; beta <- 0.5; f_cur <- 0.1 # initialization
for(i in 1:1000)
{
f_next <- abs(rnorm(1, f_cur, 0.1)) # make random step for allele frequency
LL_cur <- LL(n, f_cur); LL_next <- LL(n, f_next)
LP_cur <- LP(f_cur, alpha, beta); LP_next <- LP(f_next, alpha, beta)
hastings_ratio <- LL_next + LP_next - LL_cur - LP_cur
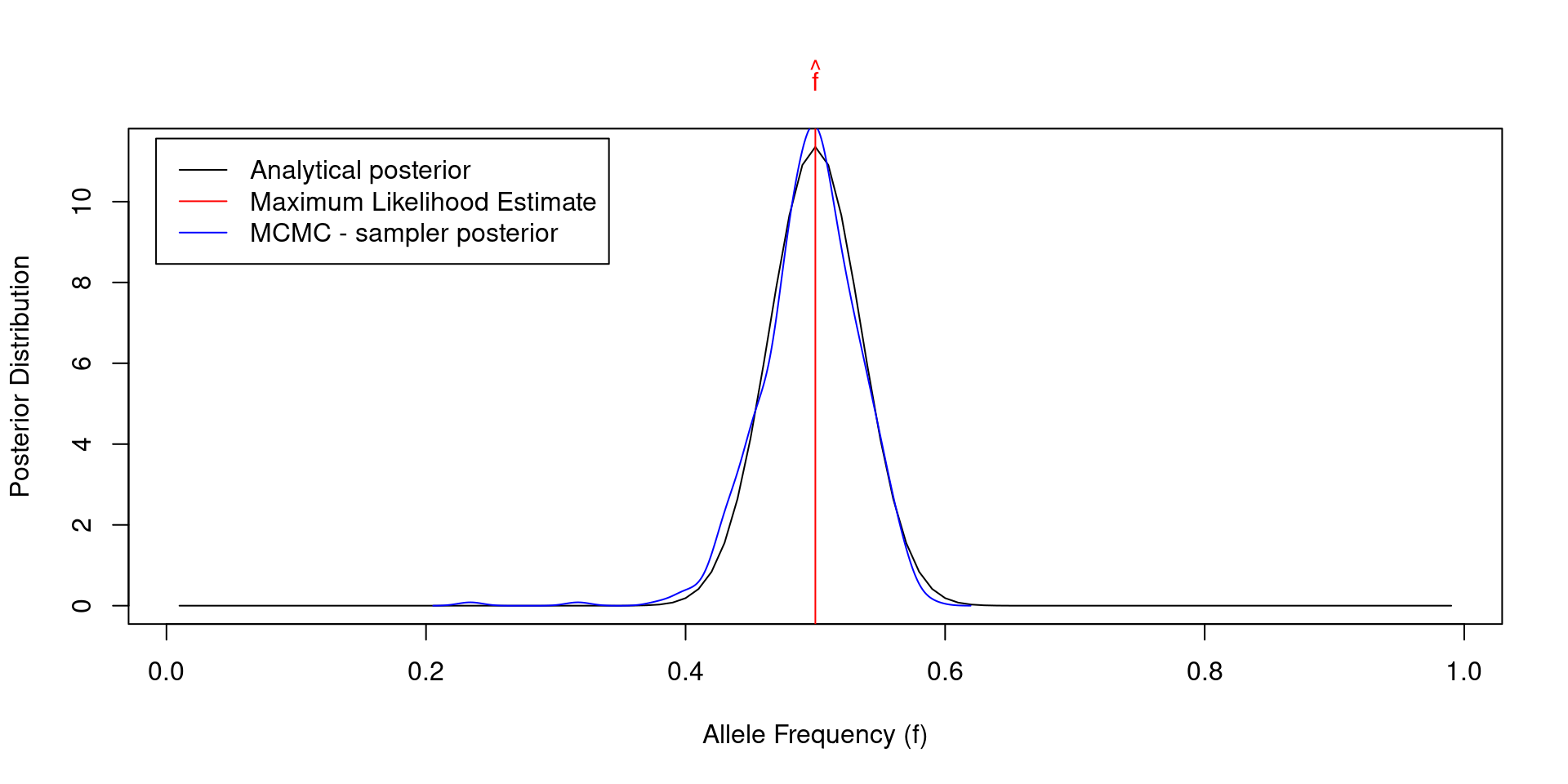
if(hastings_ratio > log(runif(1))){f_cur <- f_next}; f_poster[i] <- f_cur
}
Moving from statistics to machine learning
- Statistics is more analytical (pen & paper)
\[\rm{L}\,(\,x_i \,|\, \mu,\sigma^2\,) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp^{\displaystyle -\frac{\sum\limits_{i=1}^N (x_i-\mu)^2}{2\sigma^2}}\]
\[\frac{\partial \rm{L}\,(\,x_i \,|\, \mu,\sigma^2\,)}{\partial\mu} = 0; \,\, \frac{\partial \rm{L}\,(\,x_i \,|\, \mu,\sigma^2\,)}{\partial\sigma^2} = 0\]
\[\mu = \frac{1}{N}\sum_{i=0}^N x_i \,\,\rm{-}\,\rm{mean \, estimator}\]
\[\sigma^2 = \frac{1}{N}\sum_{i=0}^N (x_i-\mu)^2 \,\,\rm{-}\,\rm{variance \, estimator}\]
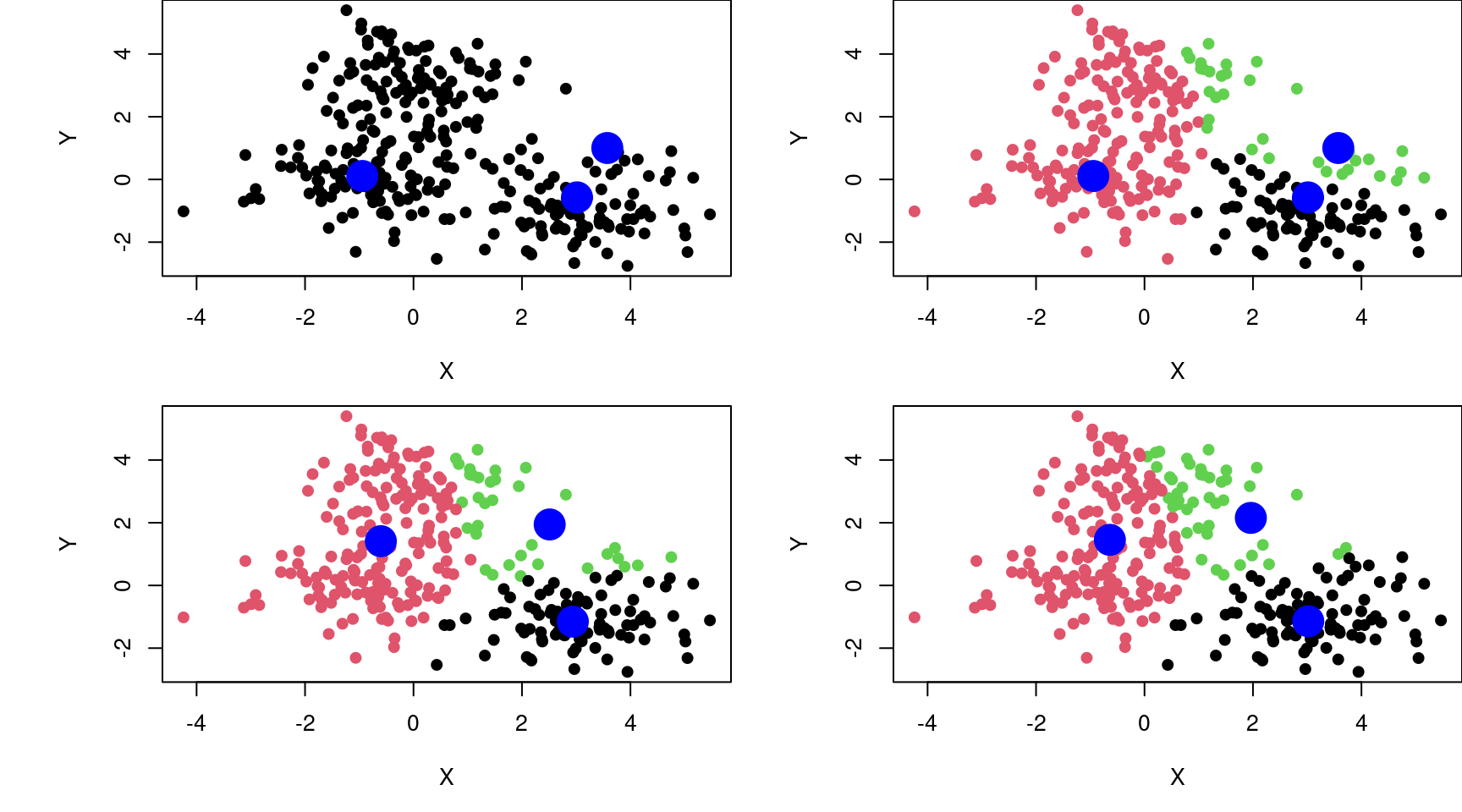
- Machine Learning is more algorithmic (ex. K-means)
K = 3; set.seed(123); c = X[sample(1:dim(X)[1],K),]; par(mfrow=c(2,2),mai=c(0.8,1,0,0))
plot(X, xlab = "X", ylab = "Y", pch = 19); points(c, col = "blue", cex = 3, pch = 19)
for(t in 1:3)
{
l <- vector()
for(i in 1:dim(X)[1])
{
d <- vector(); for(j in 1:K){d[j] <- sqrt((X[i,1]-c[j,1])^2 + (X[i,2]-c[j,2])^2)}
l[i] <- which.min(d)
}
plot(X, xlab="X", ylab="Y", col=l, pch=19); points(c, col="blue", cex=3, pch=19)
s = list(); for(i in unique(l)){s[[i]] <- colMeans(X[l==i,])}; c = Reduce("rbind", s)
}
Statistics vs. machine learning: prediction
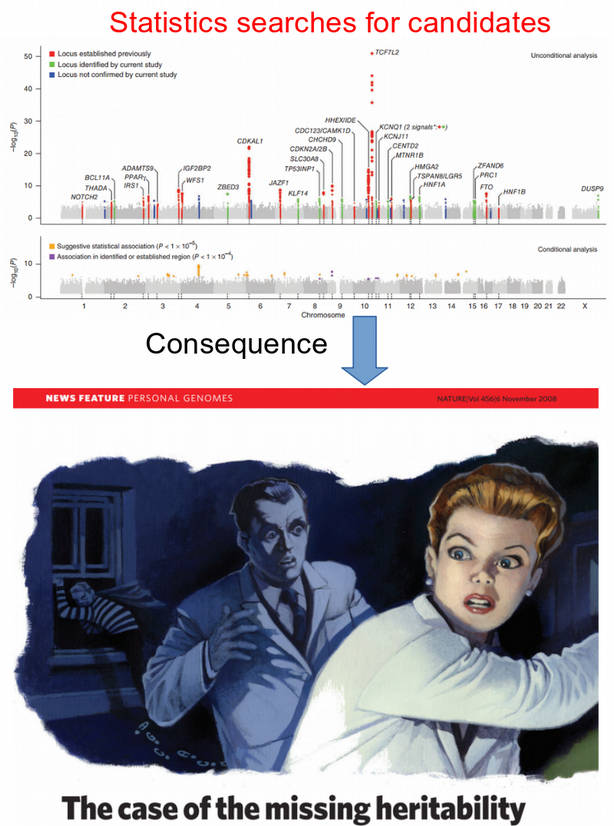

How does machine learning work?
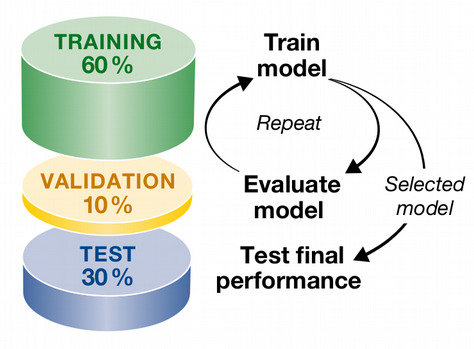
Machine Learning typically involves five basic steps:
1. Split data set into train, validation and test subsets
- Fit the model on the train subset
- Validate your model on the validation subset
- Repeat train - validation split many times and tune hyperparameters
- Test the accuracy of the optimized model on the test subset.
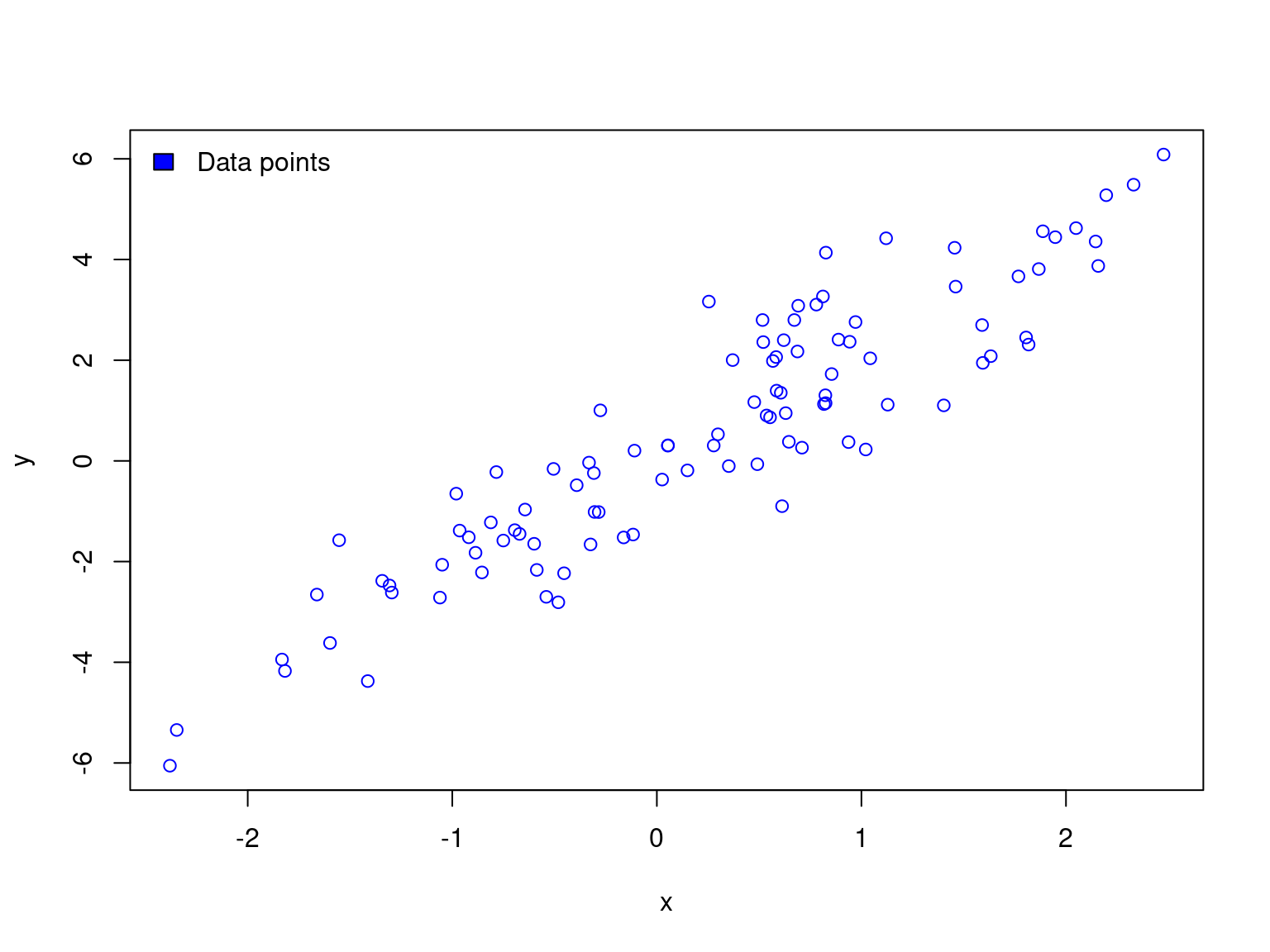
Toy example of machine learning
train <- df[sample(1:dim(df)[1], 0.7 * dim(df)[1]), ]
test <- df[!rownames(df) %in% rownames(train), ]
df$col <- ifelse(rownames(df) %in% rownames(test), "red", "blue")
plot(y ~ x, data = df, col = df$col)
legend("topleft", c("Train","Test"), fill=c("blue","red"), bty="n")
abline(lm(y ~ x, data = train), col = "blue")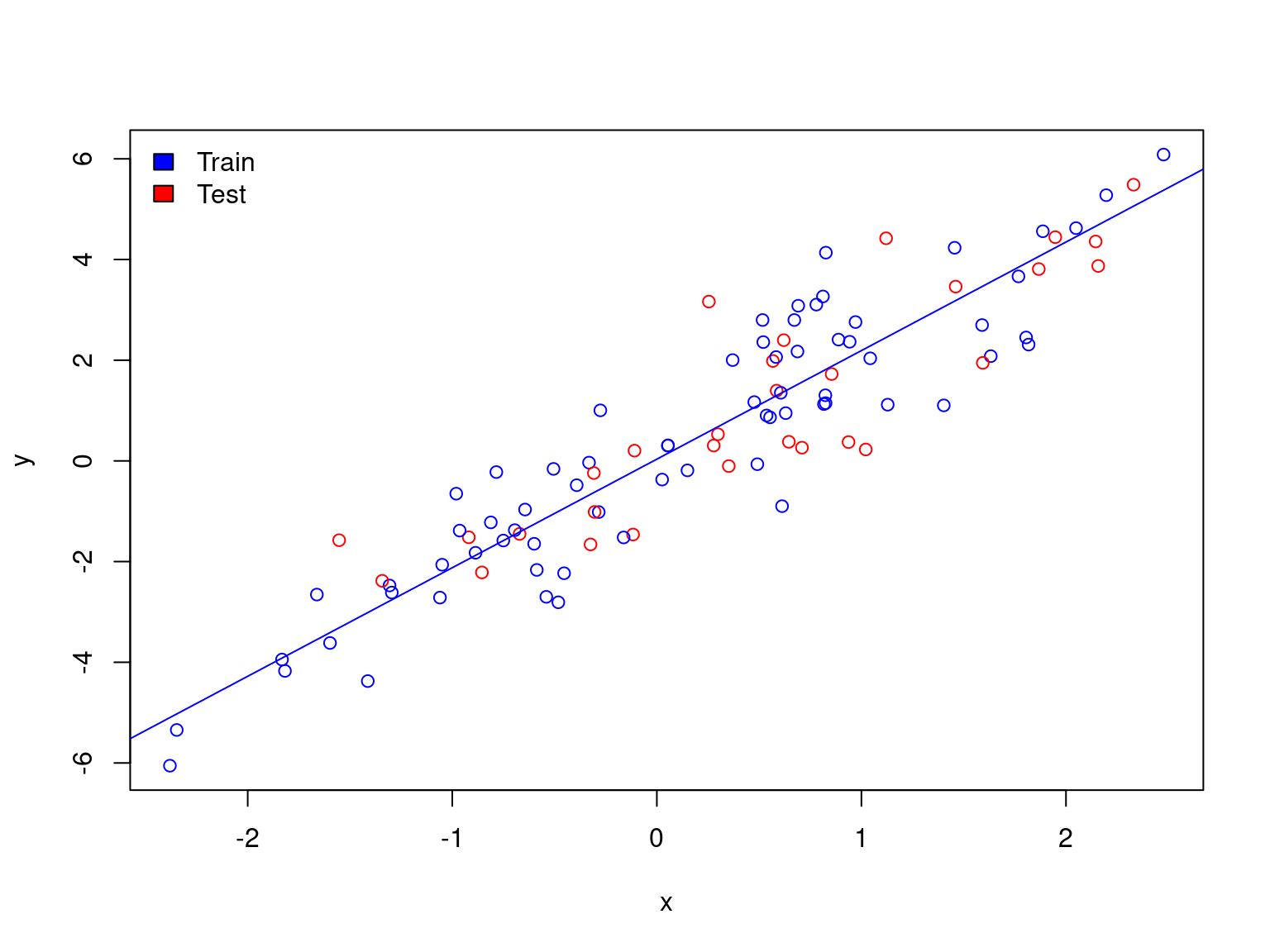
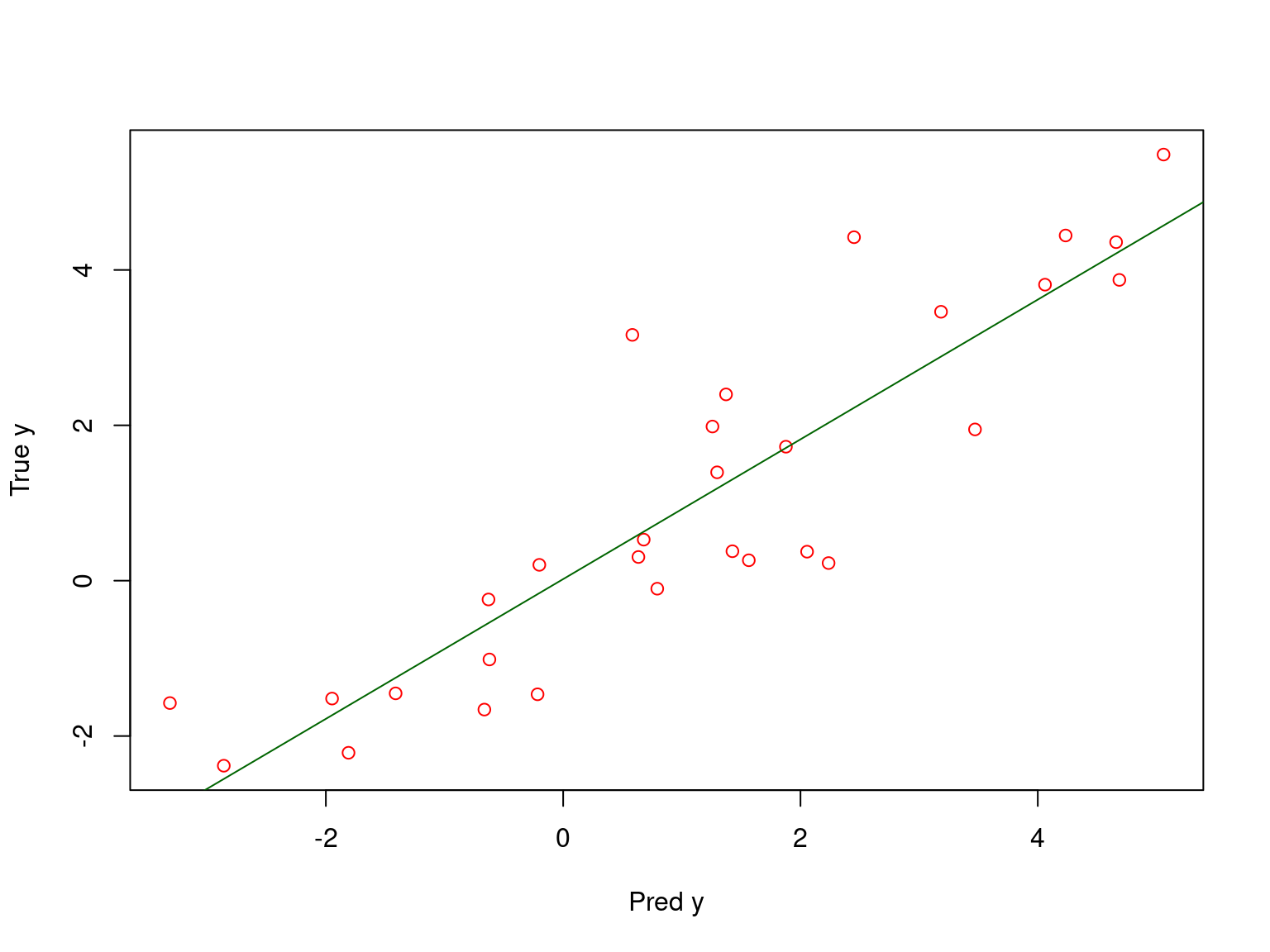
Toy example: model validation
Call:
lm(formula = test$y ~ test_predicted)
Residuals:
Min 1Q Median 3Q Max
-1.80597 -0.78005 0.07636 0.52330 2.61924
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.02058 0.21588 0.095 0.925
test_predicted 0.89953 0.08678 10.366 4.33e-11 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.053 on 28 degrees of freedom
Multiple R-squared: 0.7933, Adjusted R-squared: 0.7859
F-statistic: 107.4 on 1 and 28 DF, p-value: 4.329e-11
Thus the model explains 79% of variation on the test subset.
From linear models to artificial neural networks (ANNs)
- ANN: a mathematical function Y = f(X) with a special architecture
- Can be non-linear depending on activation function
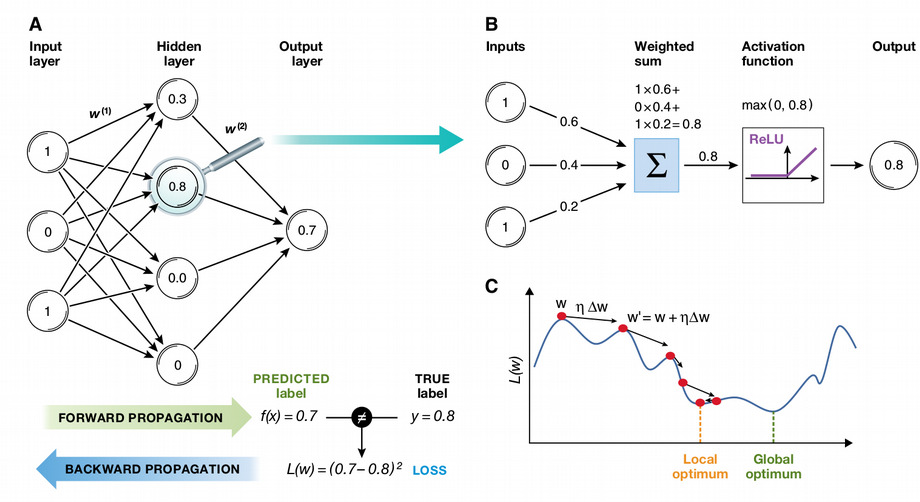
- Backward propagation (gradient descent) for minimizing error
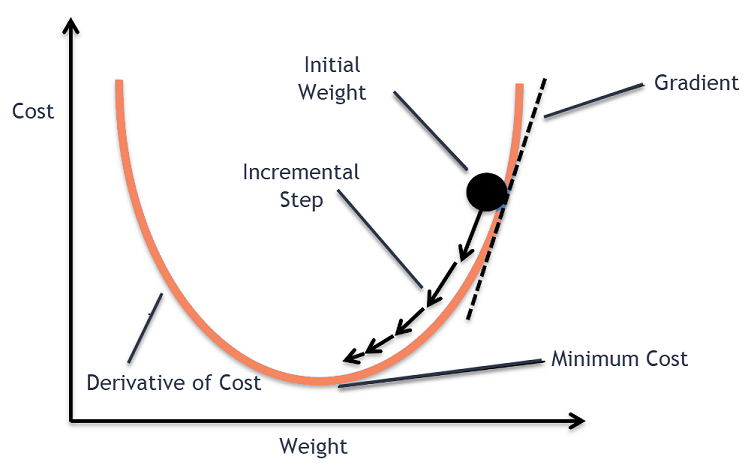
- Universal Approximation Theorem
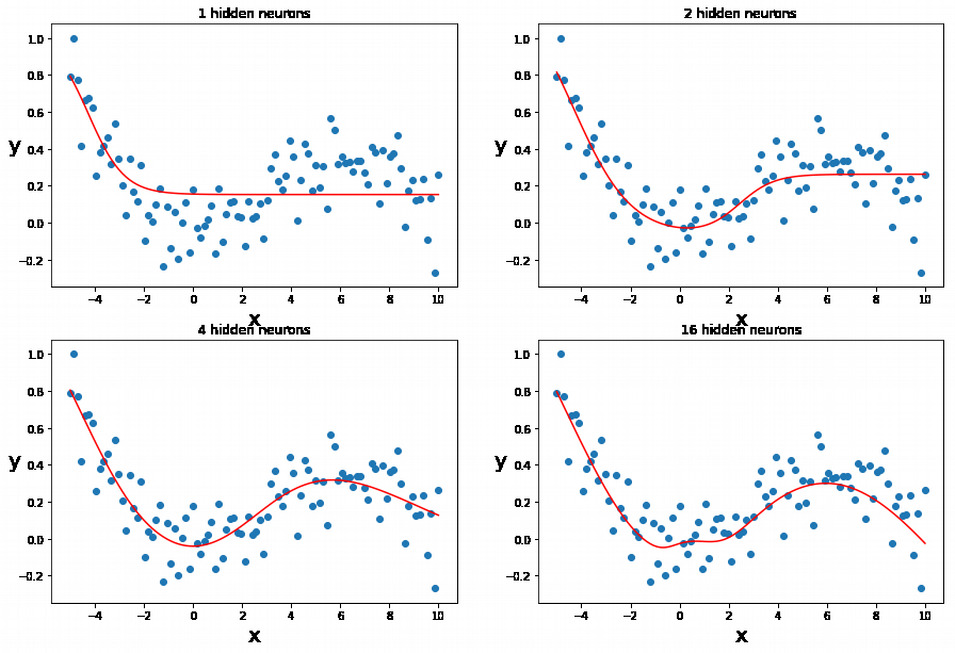
Gradient descent
\[y_i = \alpha + \beta x_i + \epsilon, \,\, i = 1 \ldots n\]
\[E(\alpha, \beta) = \frac{1}{n}\sum_{i=1}^n(y_i - \alpha - \beta x_i)^2\]
\[\hat{\alpha}, \hat{\beta} = \rm{argmin} \,\, E(\alpha, \beta)\]
\[\frac{\partial E(\alpha, \beta)}{\partial\alpha} = -\frac{2}{n}\sum_{i=1}^n(y_i - \alpha - \beta x_i)\]
\[\frac{\partial E(\alpha, \beta)}{\partial\beta} = -\frac{2}{n}\sum_{i=1}^n x_i(y_i - \alpha - \beta x_i)\]
Numeric implementation of gradient descent:
\[\alpha_{i+1} = \alpha_i - \eta \left. \frac{\partial E(\alpha, \beta)}{\partial\alpha} \right\vert_{\alpha=\alpha_i,\beta=\beta_i}\]
\[\beta_{i+1} = \beta_i - \eta \left. \frac{\partial E(\alpha, \beta)}{\partial\beta} \right\vert_{\alpha=\alpha_i,\beta=\beta_i}\]
Coding gradient descent from scratch in R
n <- 100 # sample size
x <- rnorm(n) # simulated expanatory variable
y <- 3 + 2 * x + rnorm(n) # simulated response variable
summary(lm(y ~ x))
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-1.9073 -0.6835 -0.0875 0.5806 3.2904
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.89720 0.09755 29.70 <2e-16 ***
x 1.94753 0.10688 18.22 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.9707 on 98 degrees of freedom
Multiple R-squared: 0.7721, Adjusted R-squared: 0.7698
F-statistic: 332 on 1 and 98 DF, p-value: < 2.2e-16
Let us now reconstruct the intercept and slope from gradient descent
alpha <- vector(); beta <- vector()
E <- vector(); dEdalpha <- vector(); dEdbeta <- vector()
eta <- 0.01; alpha[1] <- 1; beta[1] <- 1 # initialize alpha and beta
for(i in 1:1000)
{
E[i] <- (1/n) * sum((y - alpha[i] - beta[i] * x)^2)
dEdalpha[i] <- - sum(2 * (y - alpha[i] - beta[i] * x)) / n
dEdbeta[i] <- - sum(2 * x * (y - alpha[i] - beta[i] * x)) / n
alpha[i+1] <- alpha[i] - eta * dEdalpha[i]
beta[i+1] <- beta[i] - eta * dEdbeta[i]
}
print(paste0("alpha = ", tail(alpha, 1),", beta = ", tail(beta, 1)))[1] "alpha = 2.89719694937354, beta = 1.94752837381973"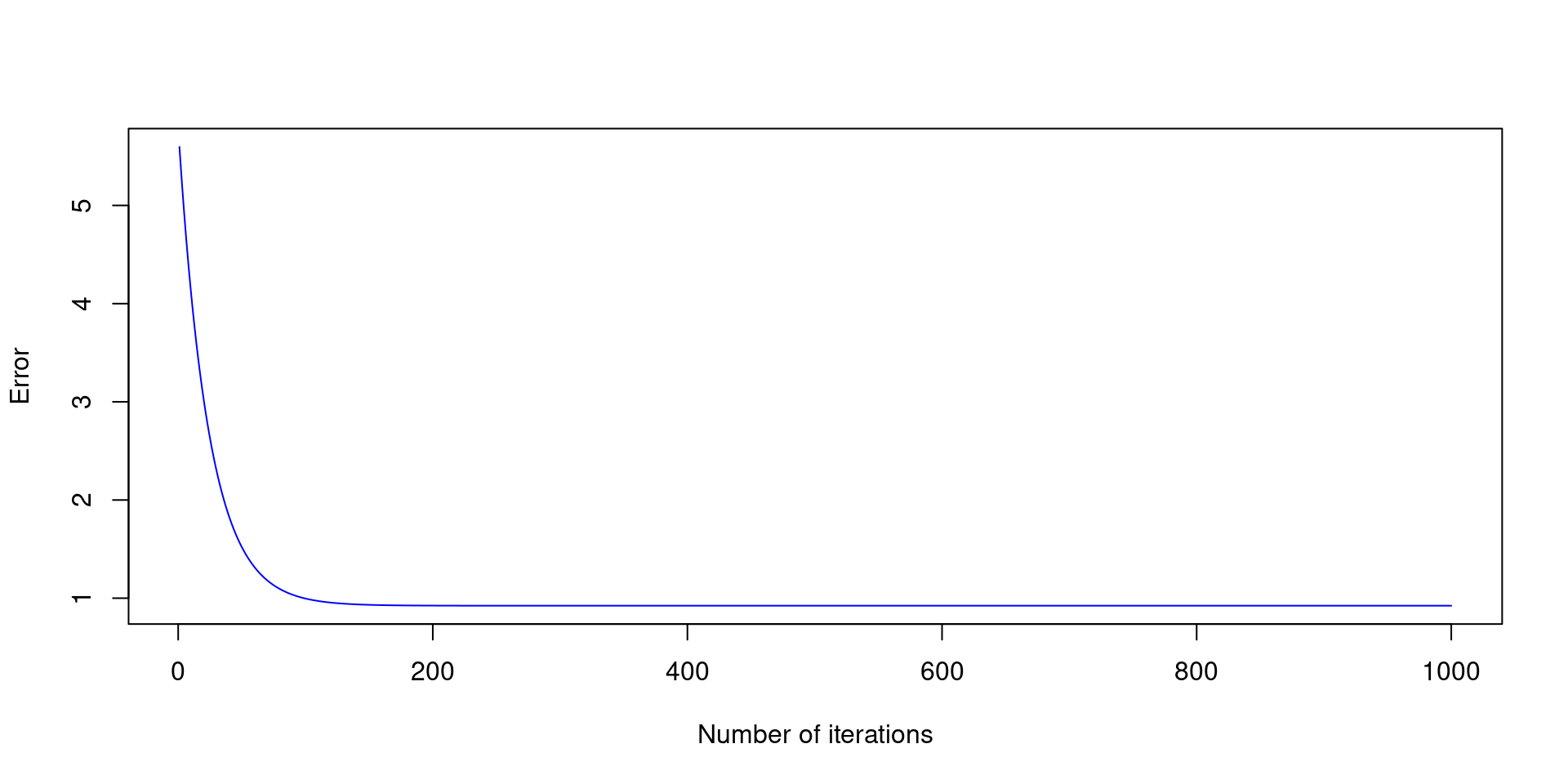
ANN from scratch in R: problem formulation
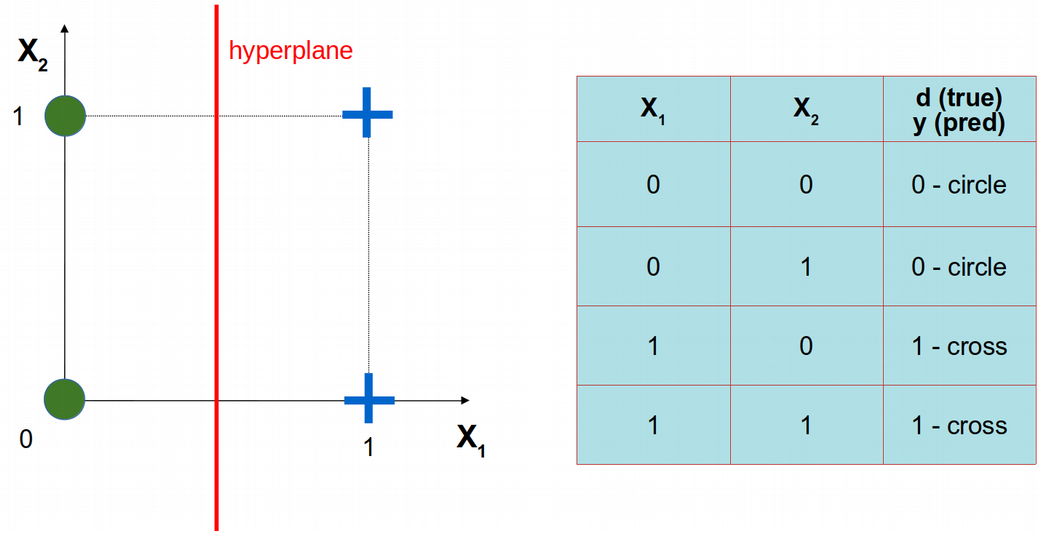
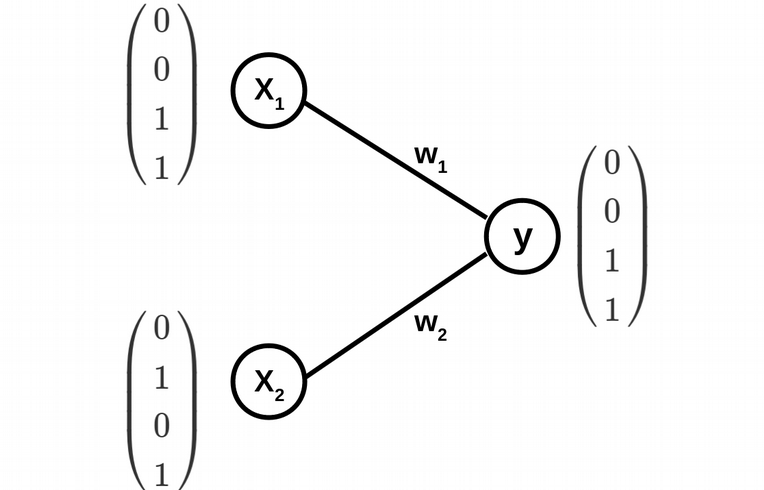
\[y(w_1,w_2)=\phi(w_1x_1+w_2x_2)\]
\[\phi(s)=\frac{1}{1+e^{\displaystyle -s}} \,\,\rm{-}\,\rm{sigmoid}\]
\[\phi^\prime(s)=\phi(s)\left(1-\phi(s)\right)\]
ANN from scratch in R: implementation in code
phi <- function(x){return(1/(1 + exp(-x)))} # activation function
mu <- 0.1; N_epochs <- 10000
w1 <- 0.1; w2 <- 0.5; E <- vector()
for(epochs in 1:N_epochs)
{
#Forward propagation
y <- phi(w1 * x1 + w2 * x2 - 3) # we use a fixed bias -3
#Backward propagation
E[epochs] <- (1 / (2 * length(d))) * sum((d - y)^2)
dE_dw1 <- - (1 / length(d)) * sum((d - y) * y * (1 - y) * x1)
dE_dw2 <- - (1 / length(d)) * sum((d - y) * y * (1 - y) * x2)
w1 <- w1 - mu * dE_dw1
w2 <- w2 - mu * dE_dw2
}
plot(E ~ seq(1:N_epochs), xlab="Epochs", ylab="Error", col="red")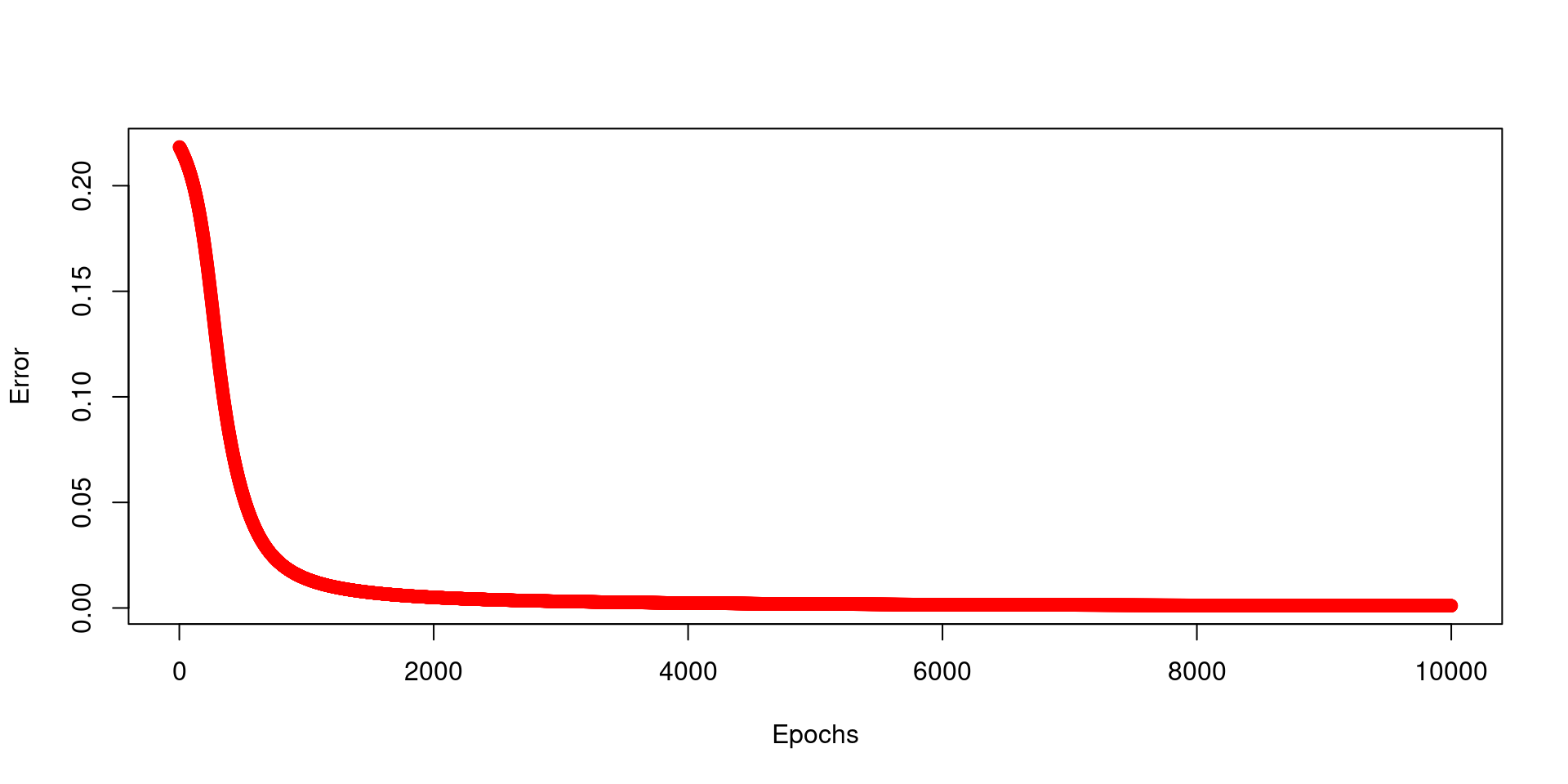
\[E(w_1,w_2)=\frac{1}{2N}\sum_{i=1}^N\left(d_i-y_i(w_1,w_2)\right)^2\]
\[w_{1,2}=w_{1,2}-\mu\frac{\partial E(w_1,w_2)}{\partial w_{1,2}}\]
\[\frac{\partial E}{\partial w_1} = -\frac{1}{N}\sum_{i=1}^N (d_i-y_i)*y_i*(1-y_i)*x_{1i}\]
\[\frac{\partial E}{\partial w_2} = -\frac{1}{N}\sum_{i=1}^N (d_i-y_i)*y_i*(1-y_i)*x_{2i}\]
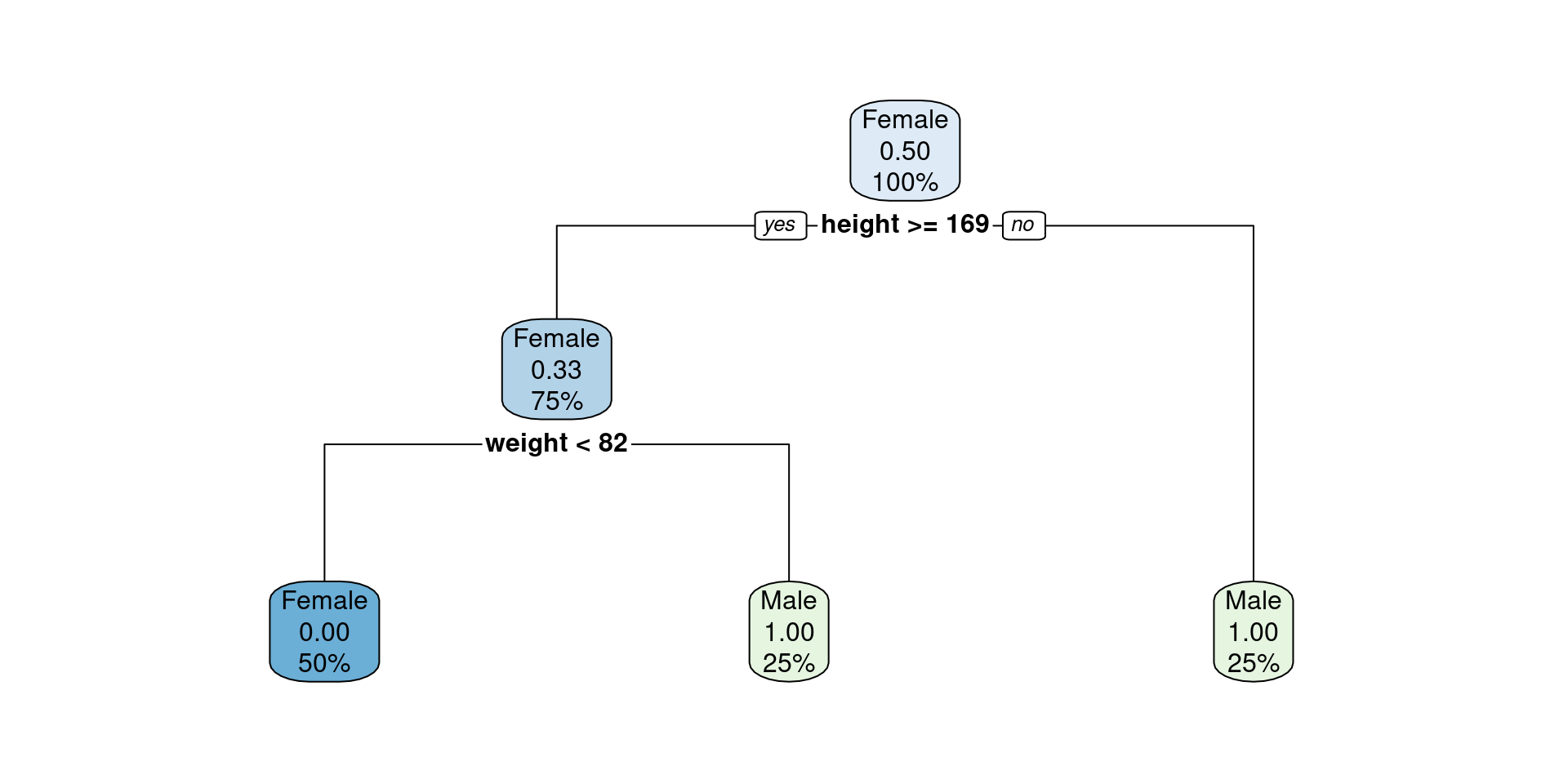
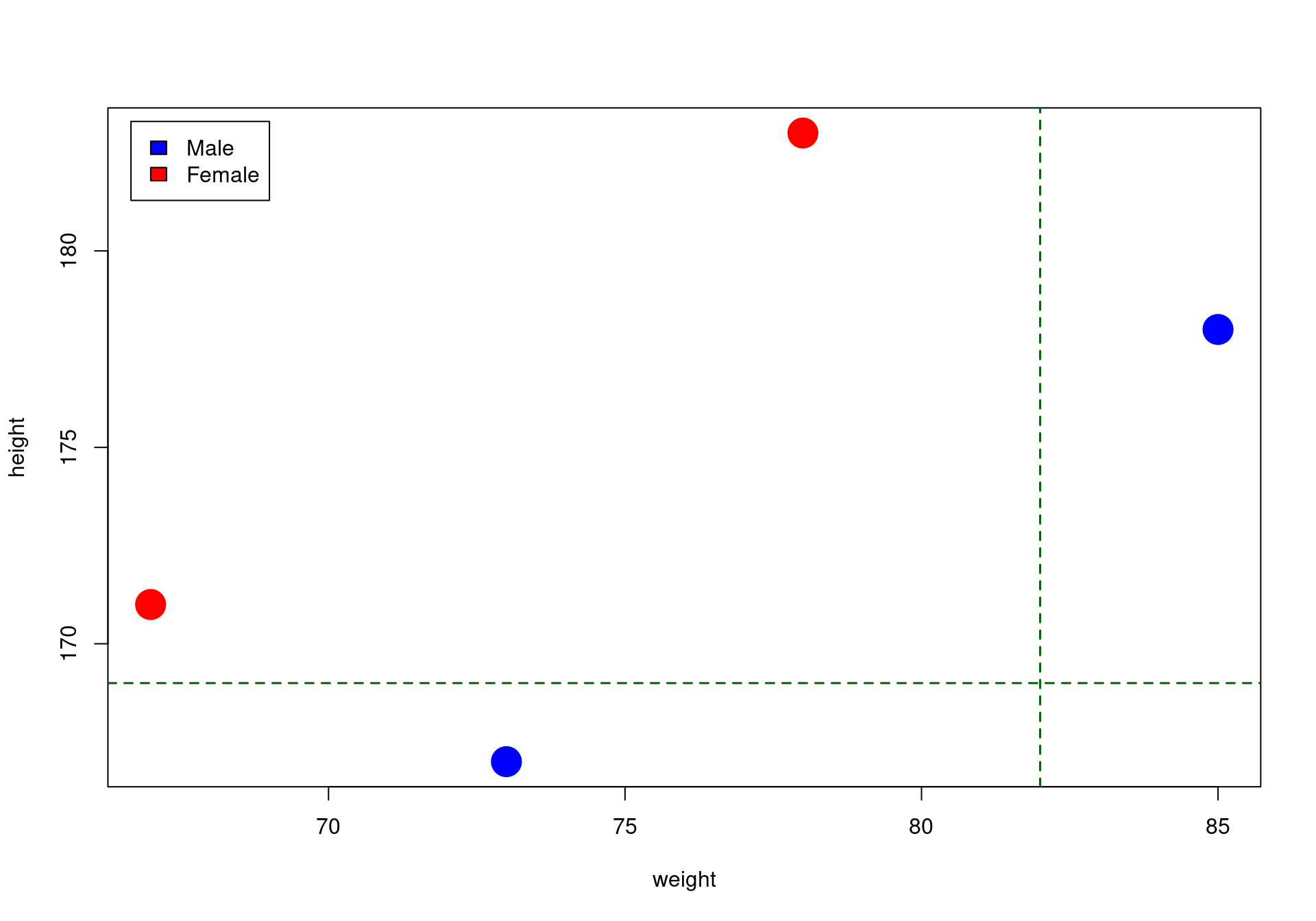
Decision tree from scratch in R: problem formulation
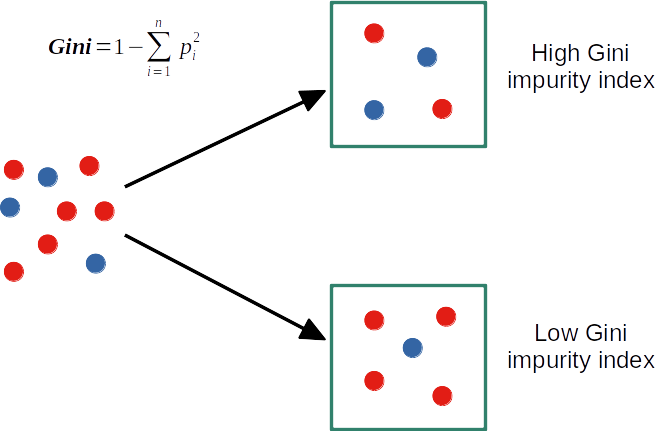
Decision tree from scratch in R: Gini index and split
get_best_split <- function(X, y)
{
mean_gini <- vector(); spl_vals <- vector(); spl_names <- vector()
for(j in colnames(X)) # for each variable in X data frame
{
spl <- vector() # vector of potential split candidates
sort_X <- X[order(X[, j]), ]; sort_y <- y[order(X[, j])] # sort by variable
for(i in 1:(dim(X)[1]-1)) # for each observation of variable in X data frame
{
spl[i] <- (sort_X[i, j] + sort_X[(i + 1), j]) / 2 # variable consecutive means
g1_y <- sort_y[sort_X[, j] > spl[i]] # take labels for group above split
g2_y <- sort_y[sort_X[, j] < spl[i]] # take labels for group below split
mean_gini <- append(mean_gini, (gini(g1_y) + gini(g2_y))/2) # two groups mean Gini
spl_vals <- append(spl_vals, spl[i])
spl_names <- append(spl_names, j)
}
}
min_spl_val <- spl_vals[mean_gini == min(mean_gini)][1] # get best split variable
min_spl_name <- spl_names[mean_gini == min(mean_gini)][1] # get best split value
sort_X <- X[order(X[, min_spl_name]), ] # sort X by best split variable
sort_y <- y[order(X[, min_spl_name])] # sort y by best split variable
g1_y <- sort_y[sort_X[, min_spl_name] > min_spl_val] # labels above best split
g2_y <- sort_y[sort_X[, min_spl_name] < min_spl_val] # labels below best split
if(gini(g1_y) == 0){sex <- paste0("Above: ", as.character(g1_y))}
else if(gini(g2_y) == 0){sex <- paste0("Below: ", as.character(g2_y))}
return(list(spl_name = min_spl_name, spl_value = min_spl_val, sex = sex))
}
get_best_split(X, y)$spl_name
[1] "height"
$spl_value
[1] 169
$sex
[1] "Below: Male"Decision tree from scratch in R: code implementation
- After we have found the best split, let us check what group we can split further: get_new_data function
get_new_data <- function(X, y)
{
spl_name <- get_best_split(X, y)$spl_name
spl_val <- get_best_split(X, y)$spl_value
# Sort X and y by the variable of the best split
sort_X <- X[order(X[, spl_name]), ]; sort_y <- y[order(X[, spl_name])]
# get X and y for the first group of samples above the best split value
g1_y <- sort_y[sort_X[, spl_name] > spl_val]
g1_X <- sort_X[sort_X[, spl_name] > spl_val,]
# get X and y for the second group of samples below the best split value
g2_y <- sort_y[sort_X[, spl_name] < spl_val]
g2_X <- sort_X[sort_X[, spl_name] < spl_val,]
# return new data (subset of X and y) for a group with Gini index > 0
if(gini(g1_y) > 0){return(list(new_X = g1_X, new_y = g1_y))}
else if(gini(g2_y) > 0){return(list(new_X = g2_X, new_y = g2_y))}
else{return(0)}
}
get_new_data(X, y)$new_X
height weight
4 171 67
3 178 85
1 183 78
$new_y
[1] Female Male Female
Levels: Female Male- We can train a decision tree of max_depth = 2
decision_tree <- function(X, y, max_depth = 2)
{
new_X <- X; new_y <- y
df <- data.frame(matrix(ncol = 5, nrow = max_depth))
colnames(df) <- c("spl_num", "spl_name", "sign", "spl_val", "label")
for(i in 1:max_depth)
{
best_split_output <- get_best_split(new_X, new_y)
sex <- unlist(strsplit(best_split_output$sex,": "))
df[i, "spl_num"] <- i
df[i, "spl_name"] <- best_split_output$spl_name
df[i, "sign"] <- ifelse(sex[1] == "Below", "<", ">")
df[i, "spl_val"] <- best_split_output$spl_value
df[i, "label"] <- sex[2]
new_data_output <- get_new_data(new_X, new_y)
if(length(new_data_output) != 1)
{
new_X <- new_data_output$new_X
new_y <- new_data_output$new_y
}
else
{
print("All terminal nodes have perfect purity")
break
}
}
return(df)
}
decision_tree(X, y)[1] "All terminal nodes have perfect purity"| spl_num | spl_name | sign | spl_val | label |
|---|---|---|---|---|
| 1 | height | < | 169.0 | Male |
| 2 | weight | > | 81.5 | Male |
Decision tree from scratch in R: prediction
- Finally, after we have trained the decision tree, we can try to make predictions, and check whether we can reconstruct the labels of the data points
predict_decision_tree <- function(X, y)
{
# Train a decision tree
t <- decision_tree(X, y, max_depth = 2)
# Parse the output of decision tree and code it via if, else if and else
pred_labs <- vector()
for(i in 1:dim(X)[1])
{
if(eval(parse(text=paste0(X[i,t$spl_name[1]],t$sign[1],t$spl_val[1]))))
{
pred_labs[i] <- t$label[1]
}
else if(eval(parse(text=paste0(X[i,t$spl_name[2]],t$sign[2],t$spl_val[2]))))
{
pred_labs[i] <- t$label[2]
}
else{pred_labs[i] <- ifelse(t$label[2] == "Male", "Female", "Male")}
}
return(cbind(cbind(X, y), pred_labs))
}
predict_decision_tree(X, y)[1] "All terminal nodes have perfect purity"| height | weight | y | pred_labs |
|---|---|---|---|
| 183 | 78 | Female | Female |
| 167 | 73 | Male | Male |
| 178 | 85 | Male | Male |
| 171 | 67 | Female | Female |
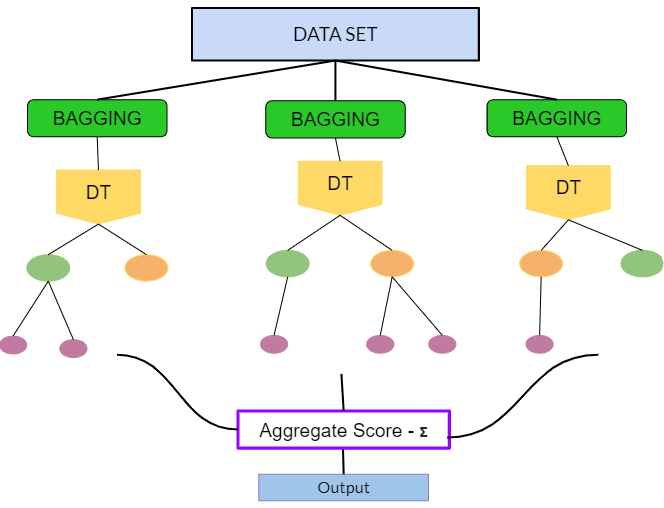
Random Forest has two key differences:
train multiple decision trees (bagging)
train trees on fractions of input features
Thank you! Questions?
_
platform x86_64-pc-linux-gnu
os linux-gnu
major 4
minor 3.2 2024 • SciLifeLab • NBIS • RaukR