1 Introduction

In this lab, we will use statistics to gain a deeper understanding and insight into the dataset. Through statistical methods, we can evaluate data quality, identify patterns, and detect any outliers that may be present. You will apply several descriptive measures to explore and summarize the dataset, allowing for a more informed analysis.

2 Generating the Data

We create a dataset which consists of:
- Two numerical variables (Normally distributed).
- Three categorical.

Note: The following chunk has a function by which you generate a random dataset (n samples with [0-100]% missing data). You can also adjust these values to create a new dataset. We will talk about functions tomorrow.

# Function to generate the data
generate_dataset <- function(n, na_frac) {
  
  # Set seed for reproducibility
  set.seed(123)
  
  # Gender variable
  Gender <- sample(c('Male', 'Female'), n, replace = TRUE)
  
  # Continuous Variable 1 with shifted distribution between genders
  Variable_1 <- ifelse(Gender == 'Male', rnorm(n, mean = 55, sd = 10), rnorm(n, mean = 45, sd = 10))
  
  # Continuous Variable 2: negative correlation with Variable_1 for one of the sexes
  Variable_2 <- ifelse(Gender == 'Male', -0.5 * Variable_1 + rnorm(n, mean = 10, sd = 5),
                       0.5 * Variable_1 + rnorm(n, mean = 10, sd = 5))
  
  # Introduce NA values (10% of the data by default)
  Variable_1[sample(1:n, round(n*na_frac))] <- NA
  Variable_2[sample(1:n, round(n*na_frac))] <- NA
  
  # Introduce outliers
  Variable_1[c(n)] <- max(Variable_1, na.rm = T) + sd(Variable_1, na.rm = T)
  Variable_1[c(round(n)/2)] <- min(Variable_1, na.rm = T) - sd(Variable_1, na.rm = T)
  
  Variable_2[c(n)] <- max(Variable_2, na.rm = T) + sd(Variable_2, na.rm = T)
  Variable_2[c(round(n)/2)] <- min(Variable_2, na.rm = T) - sd(Variable_2, na.rm = T)   
  
  # Categorical variables with more levels for Spearman correlation
  Category_1 <- sample(c('Category_A', 'Category_B', 'Category_C', 'Category_D', 'Category_E'), n, replace = TRUE)
  Category_2 <- sample(c('Group1', 'Group2', 'Group3'), n, replace = TRUE)
  
  # Create data frame
  dataset <- data.frame(Variable_1, Variable_2, Category_1, Category_2, Gender)
  return(dataset)
}

n <- 1000 # Number of samples (observation). 
na_frac <- 0.1 # Introducing missing values in the dataset. 
dataset <- generate_dataset(n, na_frac = na_frac )
  • Check the content of the dataset.
  • How many rows and columns do you have?

head(dataset)
dim(dataset)
##   Variable_1 Variable_2 Category_1 Category_2 Gender
## 1   48.98107 -17.884574 Category_E     Group3   Male
## 2   45.06301  -9.659943 Category_E     Group1   Male
## 3         NA -26.156498 Category_C     Group2   Male
## 4   51.27069  34.248513 Category_C     Group2 Female
## 5   39.90833  -6.082244 Category_B     Group1   Male
## 6   66.27214  42.492134 Category_B     Group3 Female
## [1] 1000    5

3 Measures of Central Tendency

3.1 Mean

mean_var1 <- mean(dataset$Variable_1)
mean_var2 <- mean(dataset$Variable_2)
mean_var1
mean_var2
## [1] NA
## [1] NA

  • What is the mean value of Variable_1 and Variable_2?

  • Is it NA? Why?

  • How many NA values do you find in your dataset?

n_na <- sum(is.na(dataset))
sprintf('There are %g missing values', n_na)
## [1] "There are 199 missing values"
  • Can you fix it?
    Click to expand To handle the NA values, you can set na.rm = TRUE in the function mean(x, na.rm = T), which removes the queries with NA values.
You can plot the distribution of the values by hist(). You will learn more about plots in Basic Graphics lecture.

hist(dataset$Variable_1, main = 'Distribution of Variable_1', xlab = 'Variable_1')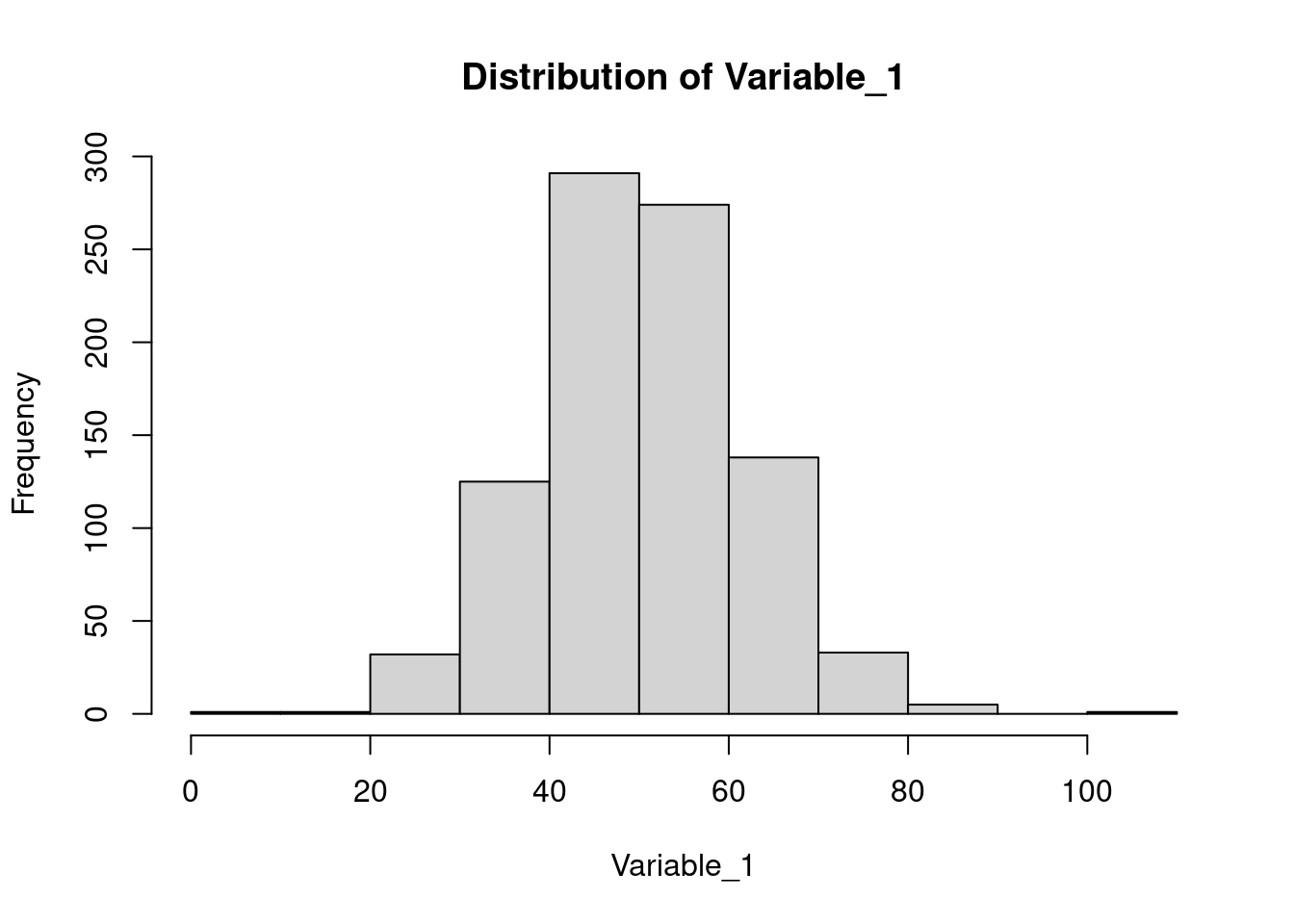
Can you create a separate histogram for each gender?

dataset_f <- dataset[(dataset$Gender == 'Female'), ]
dataset_m <- dataset[(dataset$Gender == 'Male'), ]
hist(dataset_f$Variable_1, main = 'Female', xlab = 'Variable_1')
hist(dataset_m$Variable_1, main = '', xlab = '')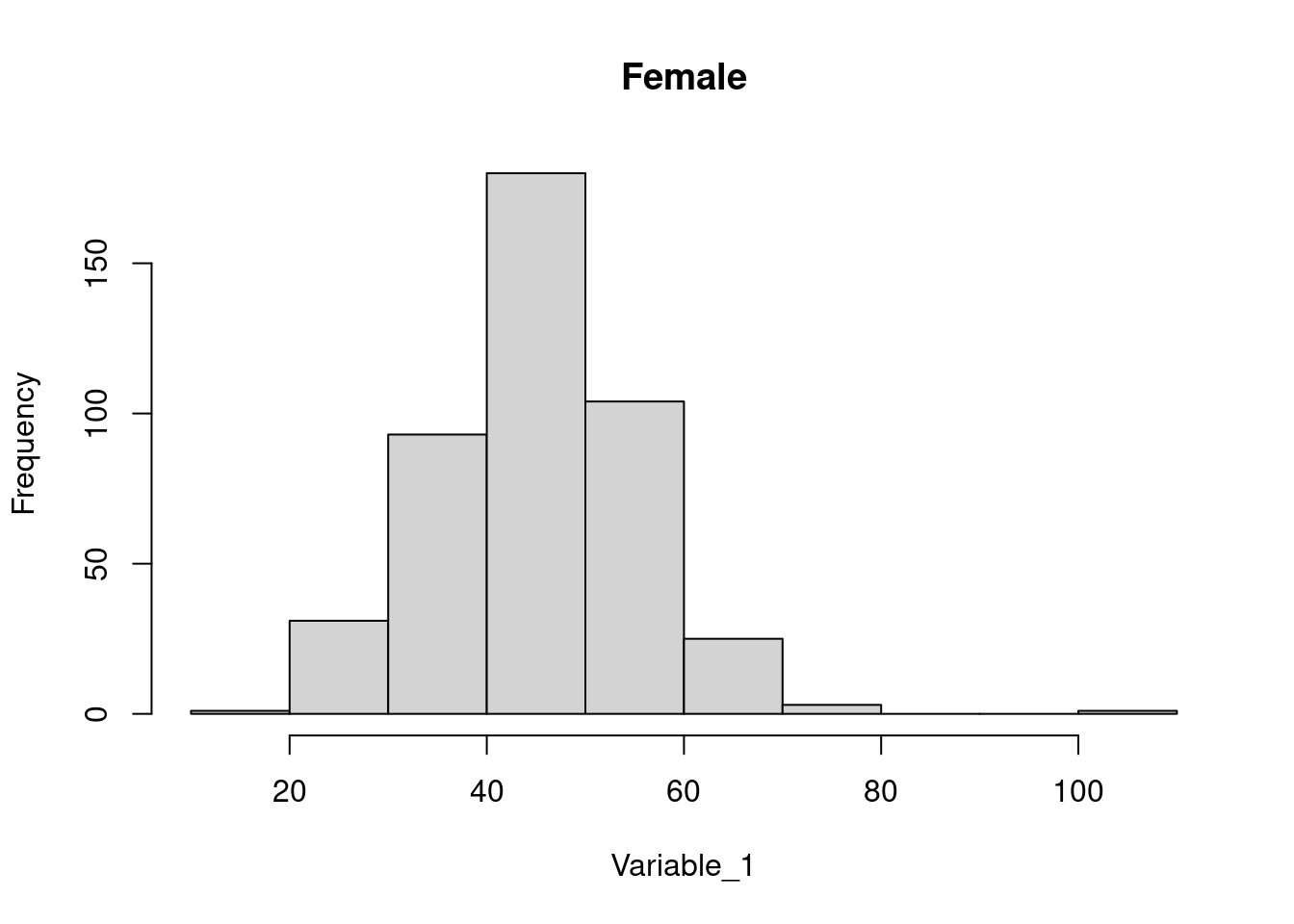

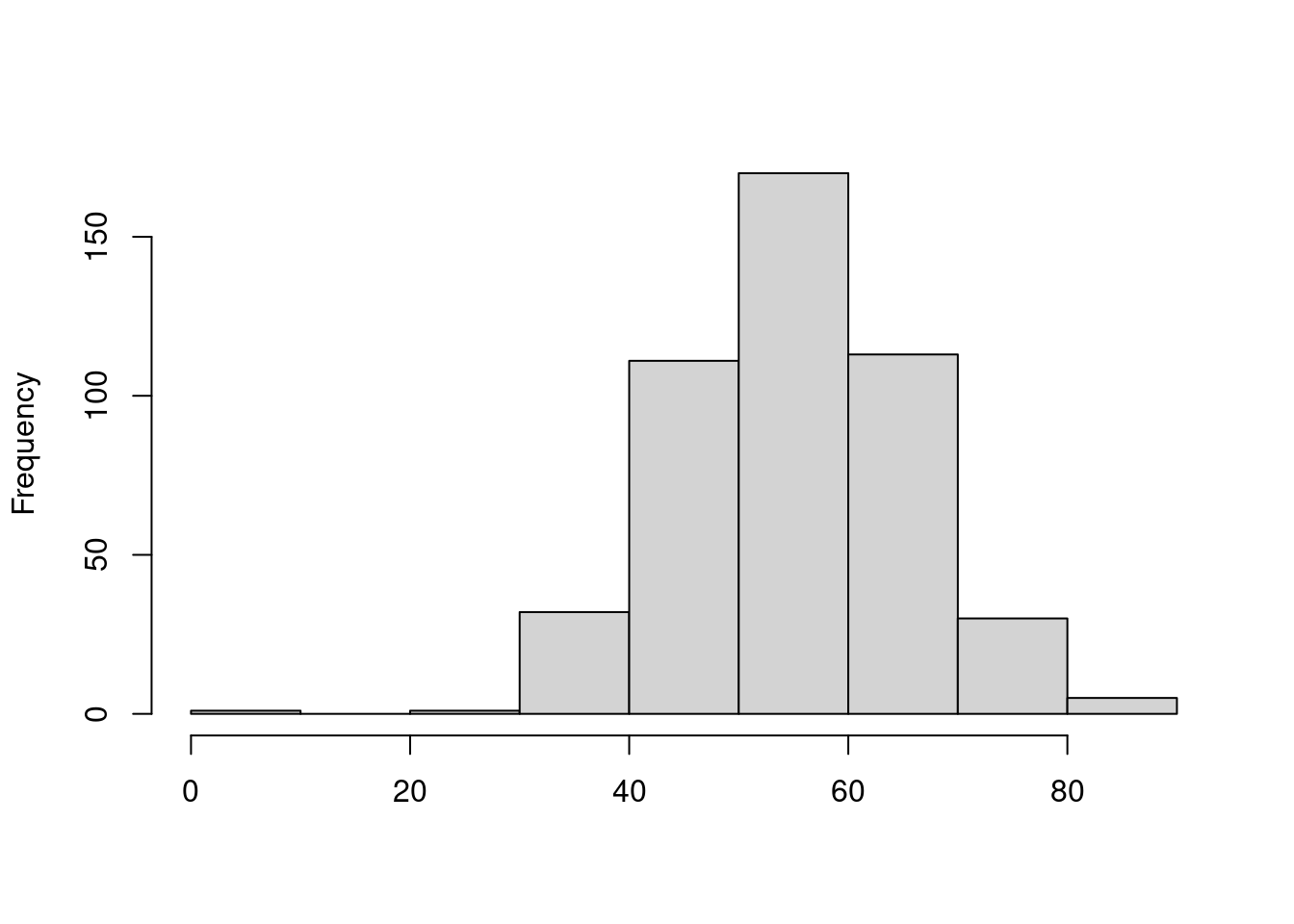
3.2 Median

median_var1 <- median(dataset$Variable_1, na.rm = T)
median_var2 <- median(dataset$Variable_2, na.rm = T)
median_var1
median_var2
## [1] 50.004
## [1] -4.740805

4 Measures of Spread

4.1 Range

We can find the range of values in numerical variables.

range_var1 <- range(dataset$Variable_1, na.rm = TRUE)
range_var2 <- range(dataset$Variable_2, na.rm = TRUE)
range_var1
range_var2
## [1]   3.119354 100.190691
## [1] -65.86148  83.70804
For categorical variables we can count the queries.

table(dataset$Category_1)
table(dataset[,c('Category_1', 'Category_2')])
table(dataset[,c('Category_1', 'Category_2', 'Gender')])
## 
## Category_A Category_B Category_C Category_D Category_E 
##        203        201        204        194        198 
##             Category_2
## Category_1   Group1 Group2 Group3
##   Category_A     80     65     58
##   Category_B     72     62     67
##   Category_C     73     71     60
##   Category_D     62     63     69
##   Category_E     64     68     66
## , , Gender = Female
## 
##             Category_2
## Category_1   Group1 Group2 Group3
##   Category_A     41     34     27
##   Category_B     35     31     30
##   Category_C     33     43     28
##   Category_D     32     32     43
##   Category_E     23     38     24
## 
## , , Gender = Male
## 
##             Category_2
## Category_1   Group1 Group2 Group3
##   Category_A     39     31     31
##   Category_B     37     31     37
##   Category_C     40     28     32
##   Category_D     30     31     26
##   Category_E     41     30     42

4.2 Interquartile.

Calculate the following for Variable_1:

  • Min.
  • Median.
  • Max.
  • Quantiles (q1:25% and q2:75%) by using quantile function.
  • Interquartile range (q3 - q1).
Note: Make sure to control for missing values (na.rm = T) 

min_val <- min(dataset$Variable_1, na.rm = T)
q1 <- quantile(dataset$Variable_1, 0.25, na.rm = T)
median_val <- median(dataset$Variable_1, na.rm = T)
q3 <- quantile(dataset$Variable_1, 0.75, na.rm = T)
max_val <- max(dataset$Variable_1, na.rm = T)
print('Variable_1 range:')
c(min_val, q1, median_val, q3, max_val)

# Interqurtile: 
print('Interquartile:')
iqr_val1 <- q3 - q1
unname(iqr_val1)
# or
iqr_val1 <- IQR(dataset$Variable_1, na.rm = T)
iqr_val1 
## [1] "Variable_1 range:"
##                   25%                   75%            
##   3.119354  42.793157  50.003998  57.990869 100.190691 
## [1] "Interquartile:"
## [1] 15.19771
## [1] 15.19771

4.3 Standard deviation

  • sd is a built-in function in R to calculate standard deviation.
  • Calculate standard deviation of Variable_1 for males and females separately.
Note: Make sure to control for missing values (na.rm = T) 

sd_var1_f <- sd(dataset_f$Variable_1, na.rm = TRUE)
sd_var1_m <- sd(dataset_m$Variable_1, na.rm = TRUE)
sd_var1_f
sd_var1_m
## [1] 10.21548
## [1] 10.56616

4.4 Variance

  • var is a built-in function in R to calculate variance.
  • Calculate variance of Variable_1 for males and females separately.
Note: Make sure to control for missing values (na.rm = T). 

var_var1_f <- var(dataset_f$Variable_1, na.rm = TRUE)
var_var1_m <- var(dataset_m$Variable_1, na.rm = TRUE)
var_var1_f
var_var1_m
## [1] 104.356
## [1] 111.6437

5 Correlation

5.1 Pearson’s correlation

  • Let’s check the correlation of Variable_1 and Variable_2 by Pearson’s method implemented in cor function. You can specify the method by method = 'pearson'.

Note: Here we handle the missing values a bit differently. In cor function, you control the missing values (NA) by setting use = 'complete.obs' which means to include observations that there are values for both variables. In other words, rows with NA in either of the values will be excluded.

pearson_correlation <- cor(dataset$Variable_1, dataset$Variable_2, use = 'complete.obs', method = "pearson")
pearson_correlation
## [1] -0.4171403
  • You can also plot the values in a simple plot using plot function. How do you interpret the results?

plot(dataset$Variable_1, dataset$Variable_2, main = 'Variable_1 vs Variable_2', xlab = 'Variable_1', ylab = 'Variable_2')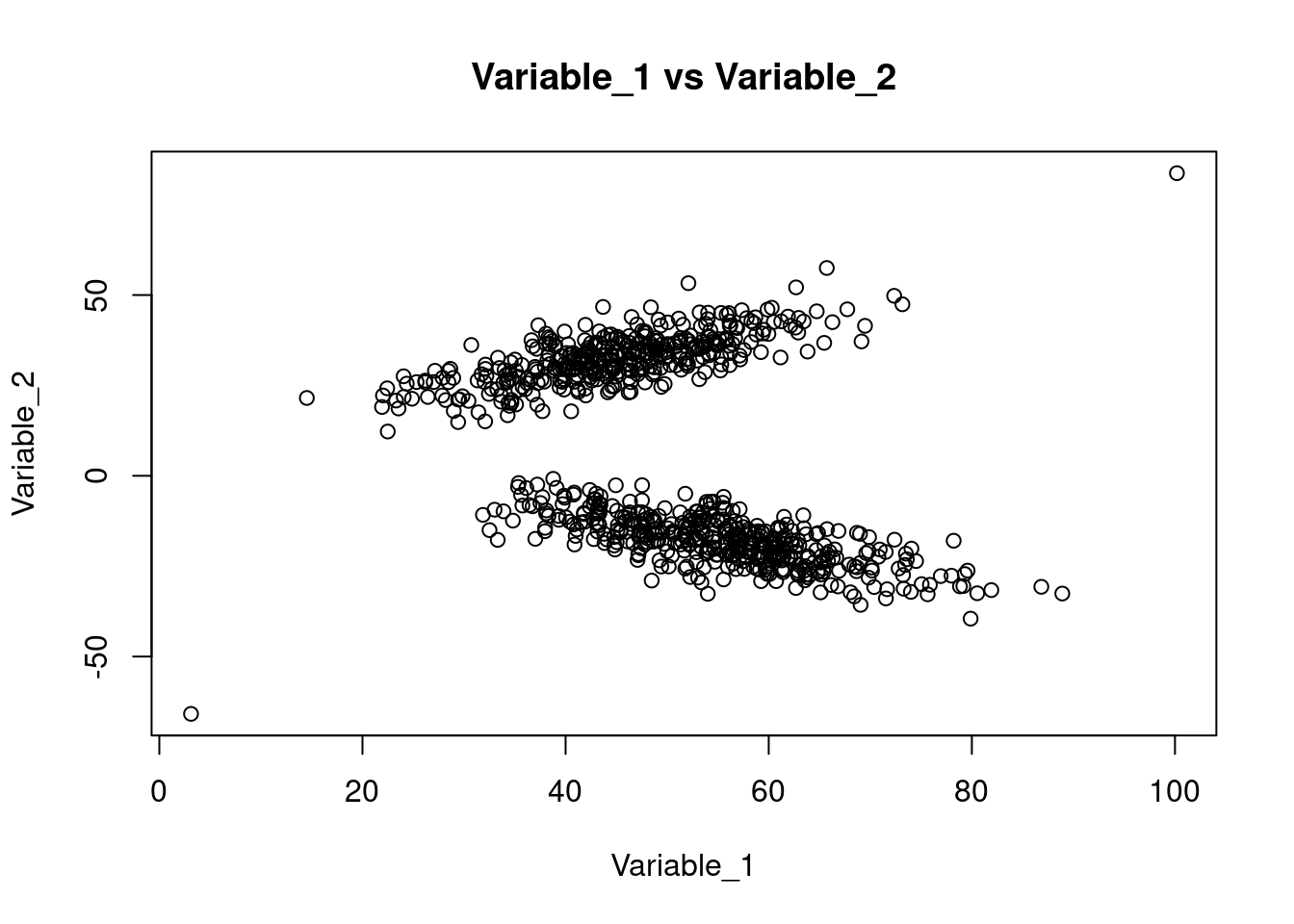

5.2 Spearman’s correlation

  • You can calculate Spearman’s correlation using the same function (cor) for both numerical and categorical data.
  • Check the result of Spearman’s correlation and Pearson’s correlation for Variable_1 and Variable_2.
  • Calculate the correlation between Category_1 and Variable_1. Consider Category_1 with ordinal variable such as level of satisfaction labeled as Category_A to E.
Note: Categorical_data cannot be directly passed to cor. You first need to encode the values as factors (the values are presented in form of levels) by as.factor. Then by converting the vector (e.g. dataset$Category_1) to numeric by as.numeric function, you can pass it to cor function.

# Spearman correlation for numerical variables
spearman_corr_numeric <- cor(dataset$Variable_1, dataset$Variable_2, use = "complete.obs", method = "spearman")

# Spearman correlation between numeric and categorical variables
spearman_corr_cat_var1 <- cor(as.numeric(as.factor(dataset$Category_1)), dataset$Variable_1, use = "complete.obs", method = "spearman")
spearman_corr_cat_var2 <- cor(as.numeric(as.factor(dataset$Category_1)), dataset$Variable_2, use = "complete.obs", method = "spearman")

spearman_corr_numeric
spearman_corr_cat_var1
spearman_corr_cat_var2
## [1] -0.4284315
## [1] 0.02013907
## [1] 0.0280211
  • Plot categorical data using plot function can be fun! If you pass the categorical as factor ( as.factor(dataset$Category_1)) together with a numerical values, you will generate a boxplot.

plot((as.factor(dataset$Category_1)), dataset$Variable_1)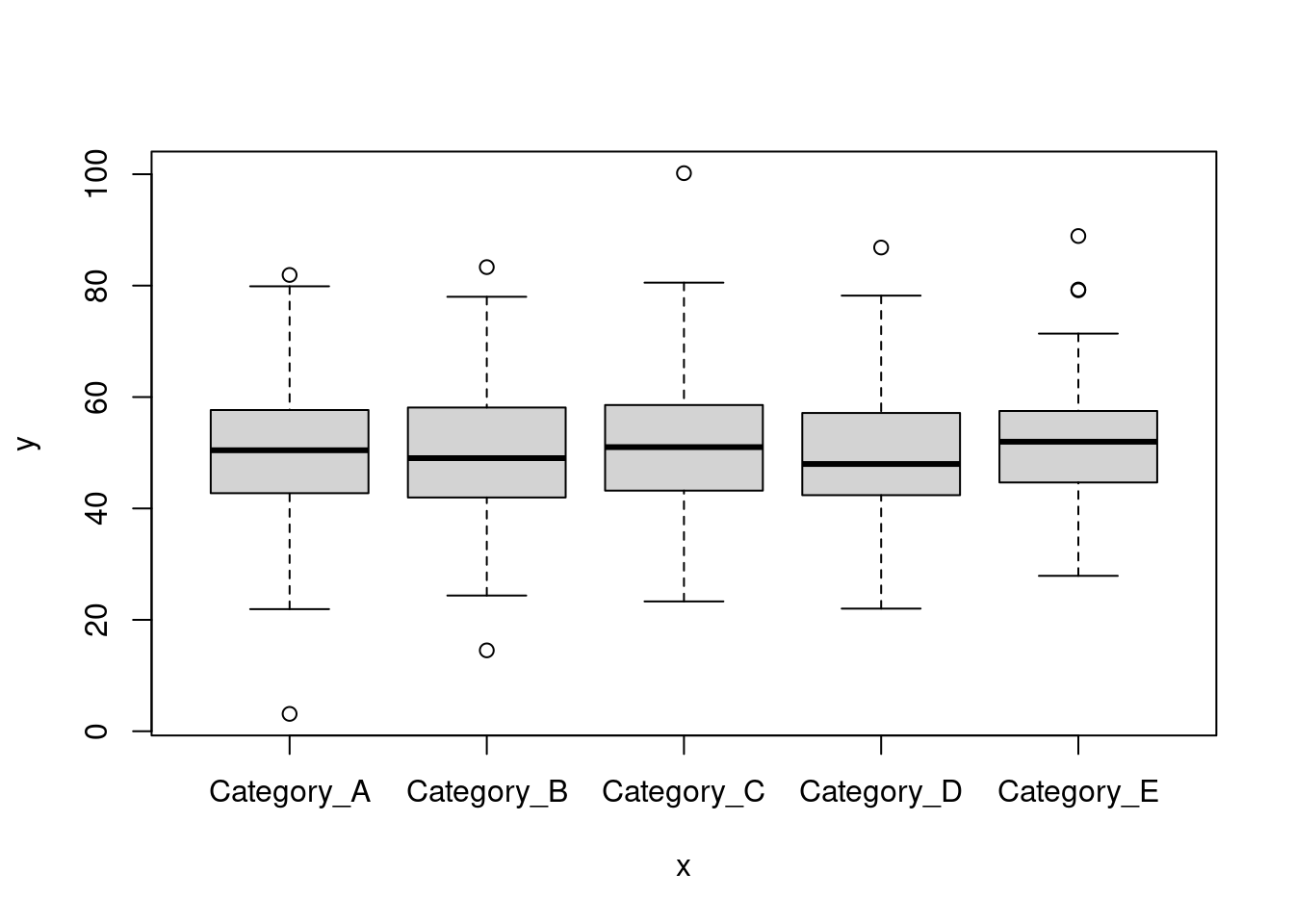

5.3 Optional exercise

  • Calculate the correlation between Gender and Variable_1, Gender as well as Variable_2.
cor_gender_var1 <- cor(as.numeric(as.factor(dataset$Gender)), dataset$Variable_1, use = 'complete.obs', method = 'spearman')
cor_gender_var2 <- cor(as.numeric(as.factor(dataset$Gender)), dataset$Variable_2, use = 'complete.obs', method = 'spearman')
cor_gender_var1
cor_gender_var2
## [1] 0.4465193
## [1] -0.8657672
  • Now plot Gender vs Variable_1 or Variable_2. How do you interpret the result?
plot((as.factor(dataset$Gender)), dataset$Variable_1)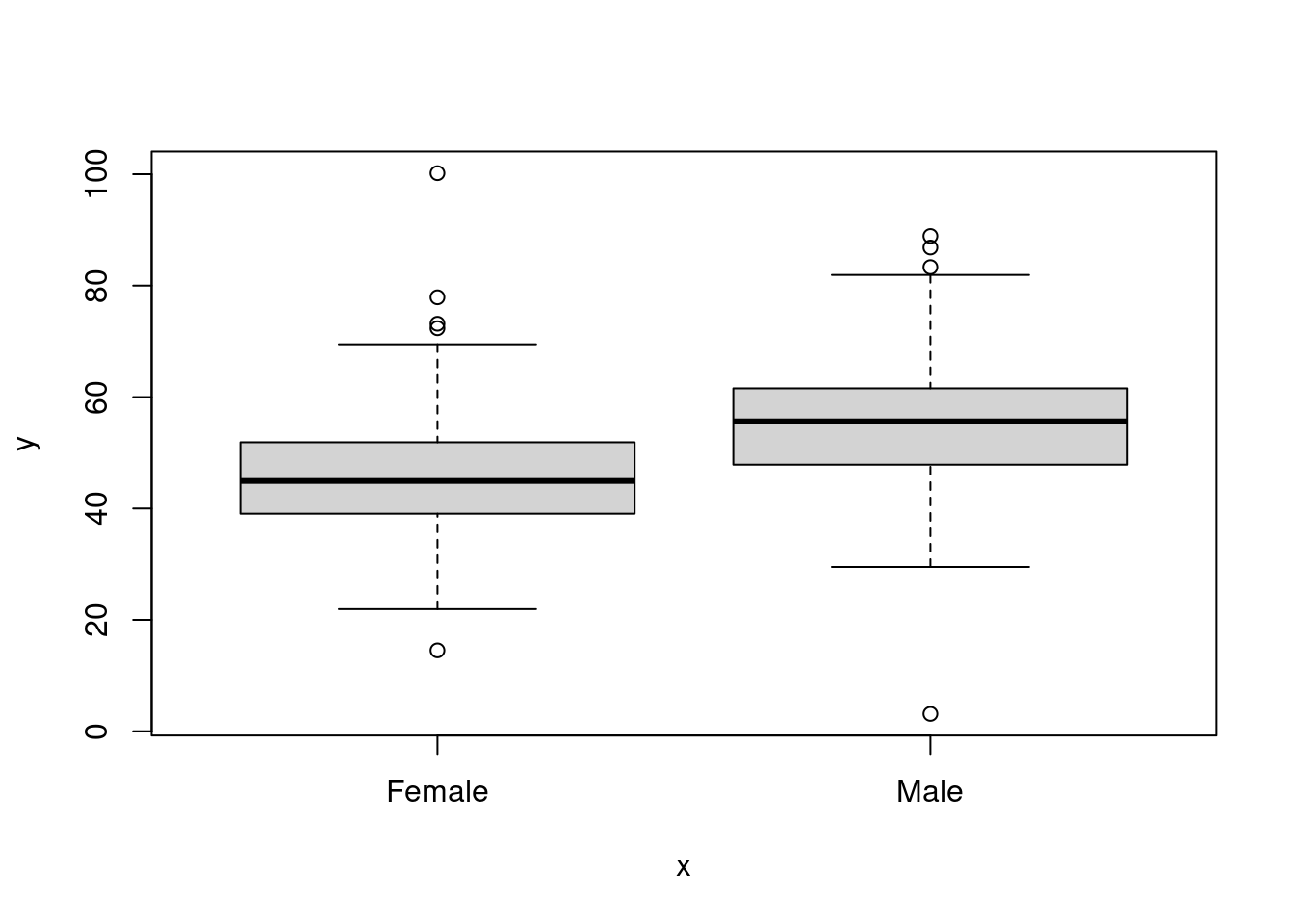

plot(as.factor(dataset$Gender), dataset$Variable_2)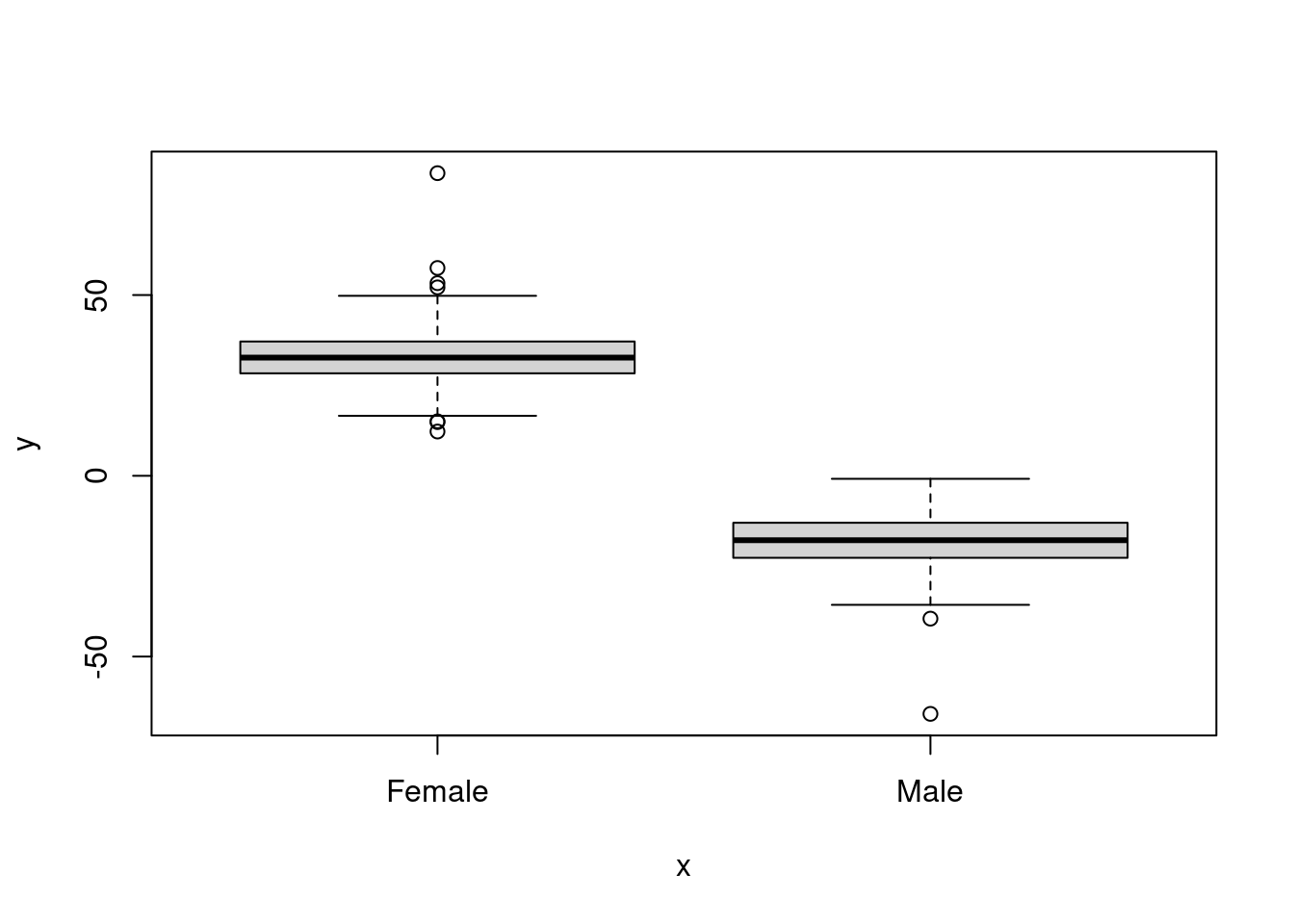

6 Bonus

You can show both histograms (males and females) in the same plot. You will learn about this in “Basic Graphics”.

par(mfrow = c(2,1), mar = c(5, 4, 1, 2) + 0.1)
range_val <- c(min(dataset$Variable_2, na.rm = T), max(dataset$Variable_2, na.rm = T) )
hist(dataset_f$Variable_2, main = 'Female', xlab = 'Variable_2', xlim = range_val, breaks = 30)
hist(dataset_m$Variable_2, main = 'Male', xlab = 'Variable_2', xlim = range_val, breaks = 30)