Primer on the coalescent and forward simulation

Per Unneberg

Intended learning outcomes

Introduction to the coalescent and simulation in msprime, with two exercises on the coalescent and msprime. The students should be able to:

• Describe need for simulations
• Demonstrate the coalescent step by step
• Detail some properties of coalescent trees
• Define the site-frequency spectrum
• Describe the coalescent with recombination
• Perform simple simulations in msprime

The Wright-Fisher model and simulations

Figure 1: Wright-Fisher model for 50 generations, 30 individuals

Recap

Model of a population describing genealogies under the following assumptions

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Forward simulation

(p. 15 Hein et al., 2005) shows the fraction of genes without descendants. Focus on the number of descendants for one gene i, which is X ~ Bin(2N, 1/2N). Since E(X)=1, for large 2N, X is almos Po(1), such that P(no descendants) = P(X=0) = e^{-1}

Low reproductive success: forward simulations costly!

The Wright-Fisher model and simulations

Figure 2: Wright-Fisher model for 50 generations, 30 individuals. Black points represent individuals that pass on offspring to the next generation.

Figure 3: Reproductive success in percent per generation.

Mean reproductive success = 63.4%. Can show for large populations P(no descendants)=1 - e^{-1} \approx 0.632

(p. 15 Hein et al., 2005) shows the fraction of genes without descendants. Focus on the number of descendants for one gene i, which is X ~ Bin(2N, 1/2N). Since E(X)=1, for large 2N, X is almos Po(1), such that P(no descendants) = P(X=0) = e^{-1}

Low reproductive success: forward simulations costly!

Forward and backward simulation

Figure 4: Forward simulation.

Figure 5: Backward simulation.

Simulated nodes are filled with black. Genealogy of interest is highlighted in thick black lines.

Forward simulations: require that we keep track of the entire population -> computationally challenging.

Backward simulations: require only tracking the sample -> quicker. However, cannot model selection.

Why do we want simulations anyway?

Null model

Generate neutral null distributions to compare with observed data

Exploration

Use to gain understanding and improve interpretation of mutational processes

Mathematical complexity

No analytical solutions for linked selection and the like \rightarrow must use simulations

Benchmarking

Use to generate test data with known properties on which to test and evaluate new methods

Model training

Generate training data for machine learning, e.g., Approximate Bayesian Computation (ABC) or Neural Networks (NNs)

The coalescent

Coalescent simulations

The coalescent simulates the genealogy of a sample of individuals on which mutations are “sprinkled” according to a Poisson process.

1. Simulate ancestry (genealogy)

NB: only the samples on the genealogy are needed, but the entire population is shown as a means to compare with forward simulations.

Coalescent simulations

The coalescent simulates the genealogy of a sample of individuals on which mutations are “sprinkled” according to a Poisson process.

1. Simulate ancestry (genealogy)
2. Simulate mutations

Coalescent simulations

The coalescent simulates the genealogy of a sample of individuals on which mutations are “sprinkled” according to a Poisson process.

1. Simulate ancestry (genealogy)
2. Simulate mutations

Exercise

How many mutations are common to all samples? How many mutations does sample 1 have? Sample 2?

Assuming the ancestral state is denoted 0 (prior to the first generation) and the derived state 1, what are the sequences of the samples?

Answers to exercise: 2 mutations are common to all samples. Sample 1 has 3 mutations, sample 2 has 4.

(arbitrarily) ordering the sites from top to bottom (oldest mutation comes first), the sequences are:

1: 11100 2: 11101 3: 11010

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes

2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes

2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2

3. Choose two chromosomes at random to coalesce

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes

2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2

3. Choose two chromosomes at random to coalesce

4. Merge the two lineages and set i \rightarrow i - 1

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2^1
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

^1: The exponential can be parametrized in two different ways, so that the parameter to the function is either \lambda or \beta=1/\lambda.

Simulating genealogies (Hahn, 2019, p. 115)

1. Start with i=n chromosomes
2. Choose time to next coalescent event from an exponential distribution with parameter \lambda=i(i-1)/2^1
3. Choose two chromosomes at random to coalesce
4. Merge the two lineages and set i \rightarrow i - 1
5. If i>1, go to step 2; if not, stop.

^1: The exponential can be parametrized in two different ways, so that the parameter to the function is either \lambda or \beta=1/\lambda.

Figure 6: A simulated genealogy. The T_i represent the waiting time when the state has i chromosomes.

Some properties of the tree

Figure 7: A coalescent tree with numbered nodes. Nodes 1-5 correspond to the samples and are leaves. The internal nodes 6-8 (and the unlabelled root) are ancestral chromosomes (unsampled). The T_i represent the waiting time when the state has i chromosomes, whereas \tau_i correspond to the branch length from node i to its parent.

The waiting time for coalescence is shorter when there are more lineages

Time to the most recent common ancestor (MRCA) (i.e., the tree height) is the sum of the waiting times (T_2 + T_3 + ...)

On average, the time for coalescence when there are two remaining lineages is half the tree height

Note that the parametrization is in 2N generations (continuous time approximation); some use N, others 4N, and so on.

Expected waiting time: the first expression follows from the fact that the waiting time, given i chromosomes, is exponentially distributed with parameter \lambda=i(i-1)/2. For an exponentially distributed variable X, the expected value is simply E(X)=1/\lambda.

Other relations are most easily derived by studying the tree and summing up relevant branches or time intervals.

Expected waiting time to coalesce when i lineages: E(T_i) = \frac{2}{i(i-1)}

Branch lengths can be derived from waiting times. For instance, \tau_1=\tau_2=T_5+T_4 and \tau_4=\tau_5=T_5

Time to the most recent common ancestor (MRCA) is sum of wating times: T_{MRCA} = \sum_{i=2}^n T_i

with expected value E(T_{MRCA}) = \sum_{i=2}^nE(T_i) = 2\left(1 - \frac{1}{n}\right)

The expected total tree height is E(T_{total}) = \sum_{i=2}^n iE(T_i) = 2\sum_{i=2}^n\frac{1}{i-1}

Coalescent simulations vary in topology and height

import msprime
seeds = [12, 15, 34, 63, 30]
trees = [msprime.sim_ancestry(3, random_seed=x) for x in seeds]

Examples of coalescent simulations. Note the variation in tree topology and height.

Diminishing returns of adding more samples

Figure 8: Dependence of time to most recent common ancestor (T_{MRCA}) and total branch length of tree on the sample size n. Already at low values of n the value of T_{MRCA} is close to its asymptotic value, which has practical consequences for the measurement of DNA variation; adding more samples mainly adds tips to the trees and does not provide access to deep time. Adapted from Wakeley (2008), Fig. 3.3.

Adding a sample only adds 2/n to the total tree length. Also, adding a sample will add little to T_{MRCA}, or equivalently, will most likely add a very recent coalescent event to the tree for large enough n. Note that n=20 here is equivalent to 10 diploid individuals.

Adding mutations

Figure 9: Adding mutations on a coalescent genealogy.

Mutations are added by “throwing” them on branches, where the probability of ending up on a given branch is equal to its relative length.

The total number of segregating sites S to be thrown on the tree is modelled as a Poisson random variable which expresses the probability of a given number of events in a given time. Here the time is the total branch length of the tree and mutations are added with intensity proportional to the population mutation rate \theta.

Sofar we have looked at genealogies; now add mutations.

In words: sample a number of segregating sites from the Poisson distribution, and “sprinkle” them on the tree.

The parametrization \lambda = \theta / 2 is defined with reference to the average heterozygosity between two sequences being \theta (by Tajima; see Wakeley (2008), p. 92)

The coalescent and diversity

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
T	T	A	C	A	A	T	C	C	G	A	T	C	G	T
T	T	A	C	G	A	T	G	C	G	C	T	C	G	T
T	C	A	C	A	A	T	G	C	G	A	T	G	G	A
T	T	A	C	G	A	T	G	C	G	C	T	C	G	T
	*			*			*			*		*		*

\begin{align} \pi & = \sum_{j=1}^S h_j = \sum_{j=1}^{S} \frac{n}{n-1}\left(1 - \sum_i p_i^2 \right) \\ & \stackrel{S=6,\\ n=4}{=} \sum_{j=1}^{6} \frac{4}{3}\left(1 - \sum_i p_i^2\right) \\ & = \frac{4}{3}\left(\mathbf{\color{#a7c947}{4}}\left(1-\frac{1}{16}-\frac{9}{16}\right) + \mathbf{\color{#a7c947}{2}}\left(1 - \frac{1}{4} - \frac{1}{4}\right)\right) = \frac{10}{3} \end{align}

In this notation one can show that \pi, the nucleotide diversity, is

\begin{equation*} \begin{split} \pi & = \frac{\sum_{i=1}^{n-1}i(n-i)\xi_i}{n(n-1)/2} \\ & \stackrel{n=4}{=} \frac{1*(4-1)*4 + 2*(4-2)*2}{6} \\ & = \frac{10}{3} \end{split} \end{equation*}

Many statistical quantities can be related to the site frequency spectrum (SFS), which is a summary of the frequencies of the segregating sites. Let \xi_i be the number of chromosomes in the sample with i minor alleles. In the example above we have S=6 mutations on n=4 chromosomes.

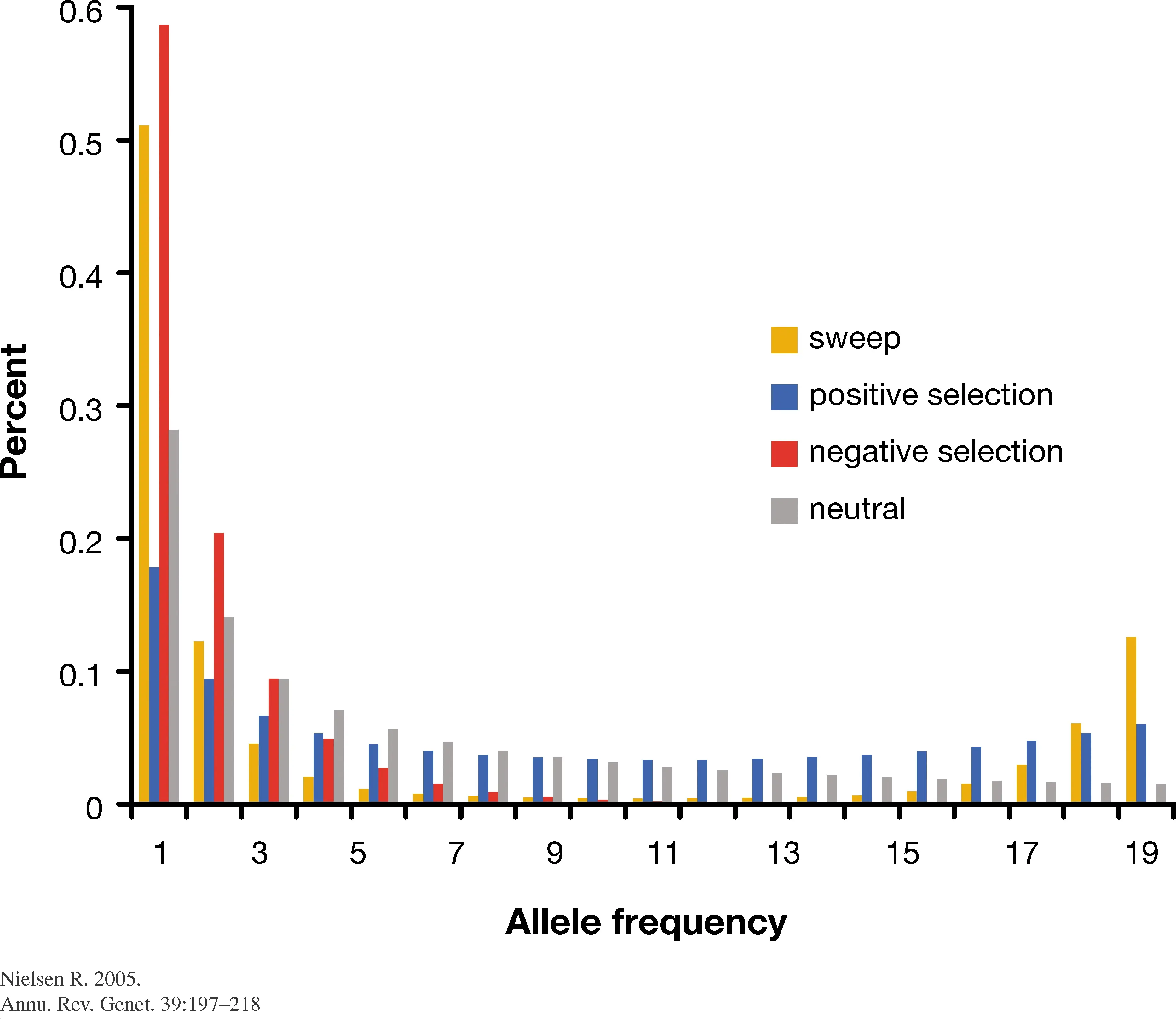
The impact of topology on the SFS

Coalescent trees.

Neutral

Expansion

Bottleneck

Selection

Figure 10: The SFS under neutrality and selection

Many tests for selection are based on the SFS which in turn is influenced by the topology of the tree.

Take home: topologies influence shape of SFS

Example: Tajima’s D

Tests common versus rare alleles. Numerator compares nucleotide diversity \pi to Watterson’s theta, \theta_W.

D < 0

recent population increase or positive selection

D > 0

population contraction or balancing selection

msprime

Jerome Kelleher

• Fast & flexible backward-time simulator
• Separates ancestry from mutation simulation
• Arbitrary discrete demographies / species
• Pedigree support (e.g., 1M+ Quebec ARG)
• Approximate extension to selective sweeps

msprime stores data as succinct tree sequences

Tree sequences (Baumdicker et al., 2022, Figure 2)

Tree sequences compress data and speedup analyses

• Compact storage (“domain specific compression”)
• Fast, efficient analysis (a “succinct” structure)
• Well tested, open source (active dev community)

Data compression

• Built-in functionality (well documented: http://tskit.dev)

…but limited support for major genomic rearrangements (e.g. inversions, large indels): genomes should be (reasonably) aligned => current primary focus = population genetics

Speed

Source: What is a tree sequence? (https://tskit.dev/tutorials/what_is.html)

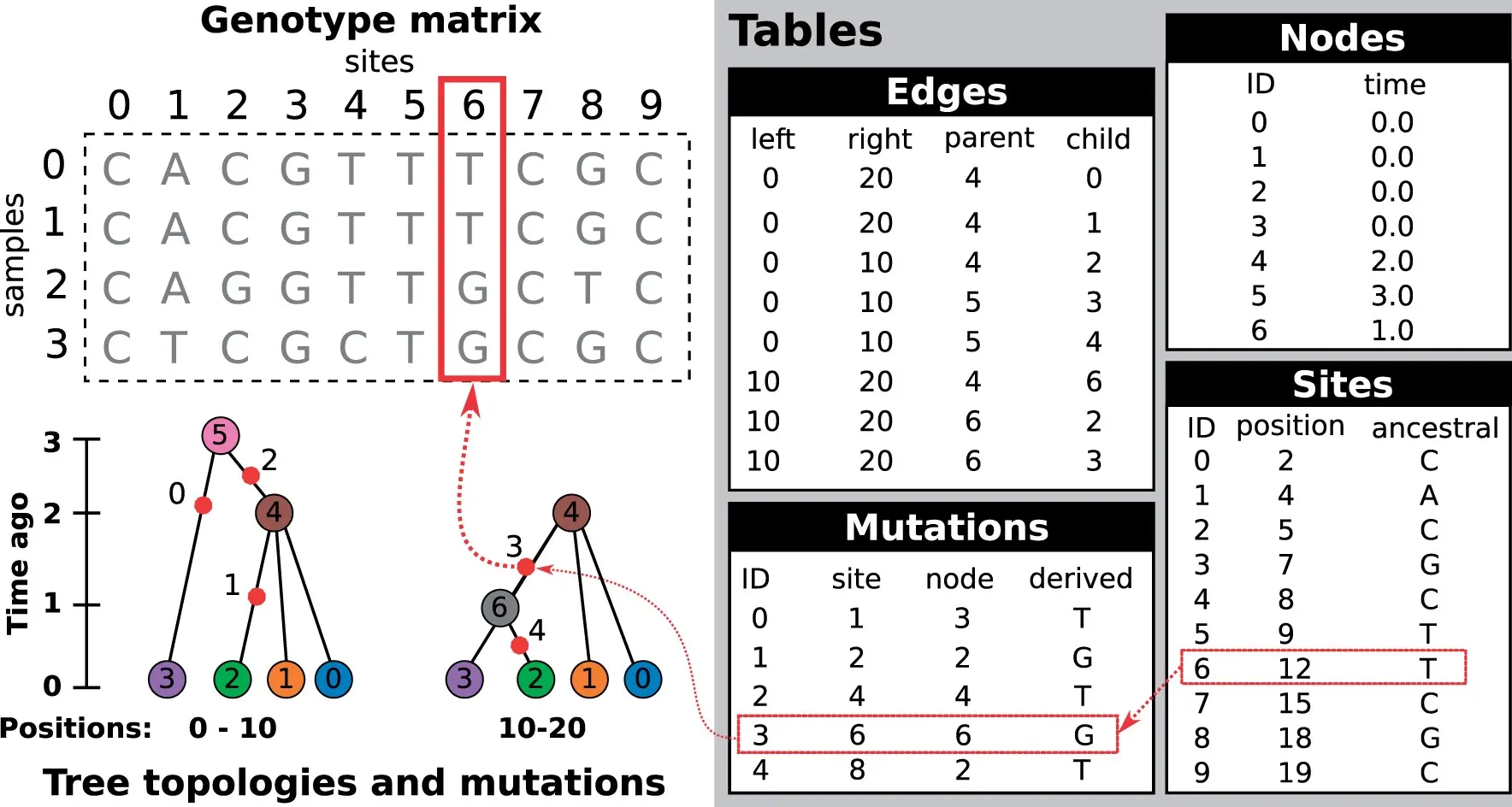
tskit terminology: the basics

• Multiple local trees exist along a genome of fixed length (by convention measured in base pairs)
• Genomes exist at specific times, and arerepresented by nodes (the same node can persist across many local trees)
• Some nodes are most recent common ancestors (MRCAs) of other nodes
• Entities are zero-based: the rst node has id 0, the second id 1, …

Images from online tutorial “Terminology & concepts” https://tskit.dev/tutorials/terminology_and_concepts.html

tskit terminology: nodes and edges

Nodes (=genomes)

• exist at a specific time
• can be flagged as “samples”
• can belong to “individuals” (e.g., 2 nodes per individuals in humans) and, if useful, “populations”

id	flags	population	individual	time	metadata
0	1	0	0	0.00000000
1	1	0	0	0.00000000
2	1	0	1	0.00000000
3	1	0	1	0.00000000
4	1	0	2	0.00000000
5	1	0	2	0.00000000
6	0	0	-1	14.70054184
7	0	0	-1	40.95936939
8	0	0	-1	72.52965866
9	0	0	-1	297.22307150
10	0	0	-1	340.15496436
11	0	0	-1	605.35907657

Edges

• Connect a parent & child
• Have a left & right genomic coordinate
• Usually span multiple trees (e.g., edges connecting nodes 1+7 and 4+7)

id	left	right	parent	child	metadata
0	0	1000	6	2
1	0	1000	6	5
2	0	1000	7	1
3	0	1000	7	4
4	0	1000	8	3
5	0	1000	8	6
6	307	1000	9	0
7	307	1000	9	7
8	0	307	10	0
9	0	567	10	8
10	307	567	10	9
11	0	307	11	7
12	567	1000	11	8
13	567	1000	11	9
14	0	307	11	10

tskit terminology: sites and mutations

This is how we can encode genetic variation. Most genomic positions do not vary between genomes: usually we don’t bother tracking these.

tskit terminology: sites and mutations

We can create a site at a given genomic position with a fixed ancestral state.

id	position	ancestral_state	metadata
0	52	C
1	200	A
2	335	A
3	354	A
4	474	G
5	523	A
6	774	C
7	796	C
8	957	A

This is how we can encode genetic variation. Most genomic positions do not vary between genomes: usually we don’t bother tracking these.

tskit terminology: sites and mutations

We can create a site at a given genomic position with a fixed ancestral state.

id	position	ancestral_state	metadata
0	52	C
1	200	A
2	335	A
3	354	A
4	474	G
5	523	A
6	774	C
7	796	C
8	957	A

This is how we can encode genetic variation. Most genomic positions do not vary between genomes: usually we don’t bother tracking these.

Normally, a site is created in order to place one or more mutations at that site

id	site	node	time	derived_state	parent	metadata
0	0	8	247.85988972	T	-1
1	1	0	169.80687857	C	-1
2	2	3	31.84262397	C	-1
3	3	9	326.26095349	C	-1
4	3	7	71.04212649	T	3
5	4	3	42.72352948	C	-1
6	5	7	55.44045835	T	-1
7	6	0	259.82567754	T	-1
8	7	8	169.87040769	G	-1
9	8	0	42.47396523	C	-1

Bibliography

Baumdicker, F., Bisschop, G., Goldstein, D., Gower, G., Ragsdale, A. P., Tsambos, G., Zhu, S., Eldon, B., Ellerman, E. C., Galloway, J. G., Gladstein, A. L., Gorjanc, G., Guo, B., Jeffery, B., Kretzschumar, W. W., Lohse, K., Matschiner, M., Nelson, D., Pope, N. S., … Kelleher, J. (2022). Efficient ancestry and mutation simulation with msprime 1.0. Genetics, 220(3), iyab229. https://doi.org/10.1093/genetics/iyab229

Hahn, M. (2019). Molecular Population Genetics (First). Oxford University Press.

Hein, J., Schierup, M. H., & Wiuf, C. (2005). Gene genealogies, variation and evolution: A primer in coalescent theory. Oxford University Press. https://books.google.se/books?id=CCmLNAEACAAJ

Wakeley, J. (2008). Coalescent Theory: An Introduction (1st Edition edition). Roberts and Company Publishers.