Admixture

Per Unneberg
Nikolay Oskolkov

Admixture: underlying assumptions


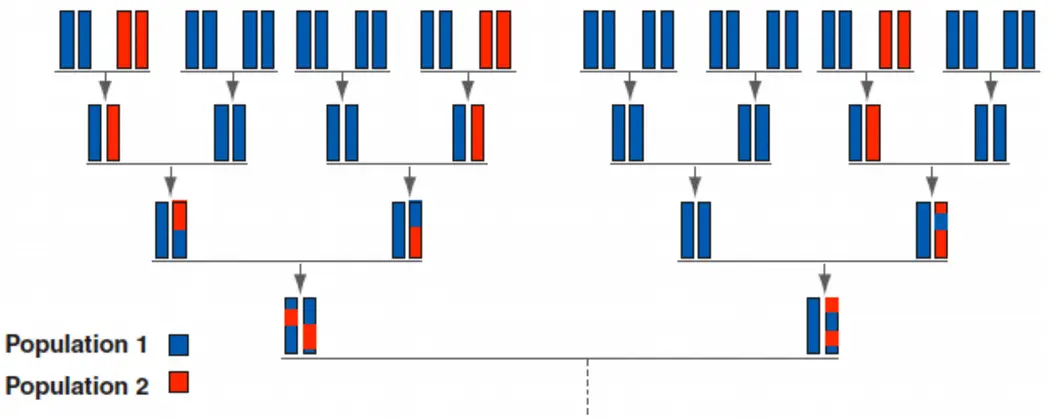
  • genetic clustering algorithm
  • at least two unadmixed populations
  • at least one admixed population
  • Maximum Likelihood: ADMIXTURE
  • Bayesian: STRUCTURE
  • delivers admixture proportions Q
  • delivers allele frequencies F for all loci for all K populations

Genotype matrices and data

Code genotypes as integers (we count the number of derived alleles per genotype):

AA\rightarrow 0 Aa\rightarrow 1 aa\rightarrow 2

Let G_i denote a single row: genotype of individual i

Genotype clustering

Early work performed hierarchical clustering on row-wise differences.

Simple idea that clustered individuals to continent.

(Mountain & Cavalli-Sforza, 1997)

The admixture model

Population matrix

Figure 1: The allele frequency matrix P. Each entry p_{kl} records the population frequency of SNP l in population k.

Assumptions:

  • within populations SNPs are in HWE
  • linkage equilibrium between remote SNPs

We also assume K populations, L SNPs and record allele frequencies in P

Figure 2: The allele frequency matrix, Q. Each entry q_{ik} denotes the ancestry component of individual i from population k

Q is the ancestry matrix. The row Q_i corresponds to the ancestry components of an individual.

A generative model

We want to model the genotypes of an individual given ancestry components and population allele frequencies.

No admixture

Assume no admixture, e.g., Q={0,0,0,1,0}

Genotype at SNP l results from sampling genotypes from the corresponding population allele frequency.

Figure 3: Individual is from population k=4. Sample genotypes from corresponding population entry.

Admixture

Now an individual has ancestry from multiple populations. First therefore it must sample the population, and given the population, can sample random genotypes from the population entry. Here we assume Q_i={0,0.25,0,0.75,0}.

Figure 4: First pick the population of origin given Q_i, then sample genotype given the population allele frequencies

Here we assume P, Q known - we could for instance use compiled databases of population allele frequencies. But we can estimate P and Q directly from data - and this is what software packages ADMIXTURE(Alexander et al., 2009) and STRUCTURE(Pritchard et al., 2000) do.

Admixture in practice

Admixture in practice

Don’t overinterpret admixture bar plots

Figure 5: Three scenarios giving indistinguishable ADMIXTURE results. From (Lawson et al., 2018, Figure 2)

Bibliography

Alexander, D. H., Novembre, J., & Lange, K. (2009). Fast model-based estimation of ancestry in unrelated individuals. Genome Research, 19(9), 1655–1664. https://doi.org/10.1101/gr.094052.109
Lawson, D. J., van Dorp, L., & Falush, D. (2018). A tutorial on how not to over-interpret STRUCTURE and ADMIXTURE bar plots. Nature Communications, 9(1), 3258. https://doi.org/10.1038/s41467-018-05257-7
Mountain, J. L., & Cavalli-Sforza, L. L. (1997). Multilocus Genotypes, a Tree of Individuals, and Human Evolutionary History. The American Journal of Human Genetics, 61(3), 705–718. https://doi.org/10.1086/515510
Pritchard, J. K., Stephens, M., & Donnelly, P. (2000). Inference of population structure using multilocus genotype data. Genetics, 155(2), 945–959. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1461096/