The Wright-Fisher model

Of population models and genealogies

Per Unneberg

Models of populations

Segue: take a step back to the days before the nature of genetic inheritance was known. First focus on the population.

Goal of lecture is also to understand genetic relationships in the context of genealogies -> coalescent.

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

See Hein et al. (2004) for more assumptions. The second assumption means we can use 2N chromosome interchangeably for haploid (n=2N) and diploid (n=N) populations.

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

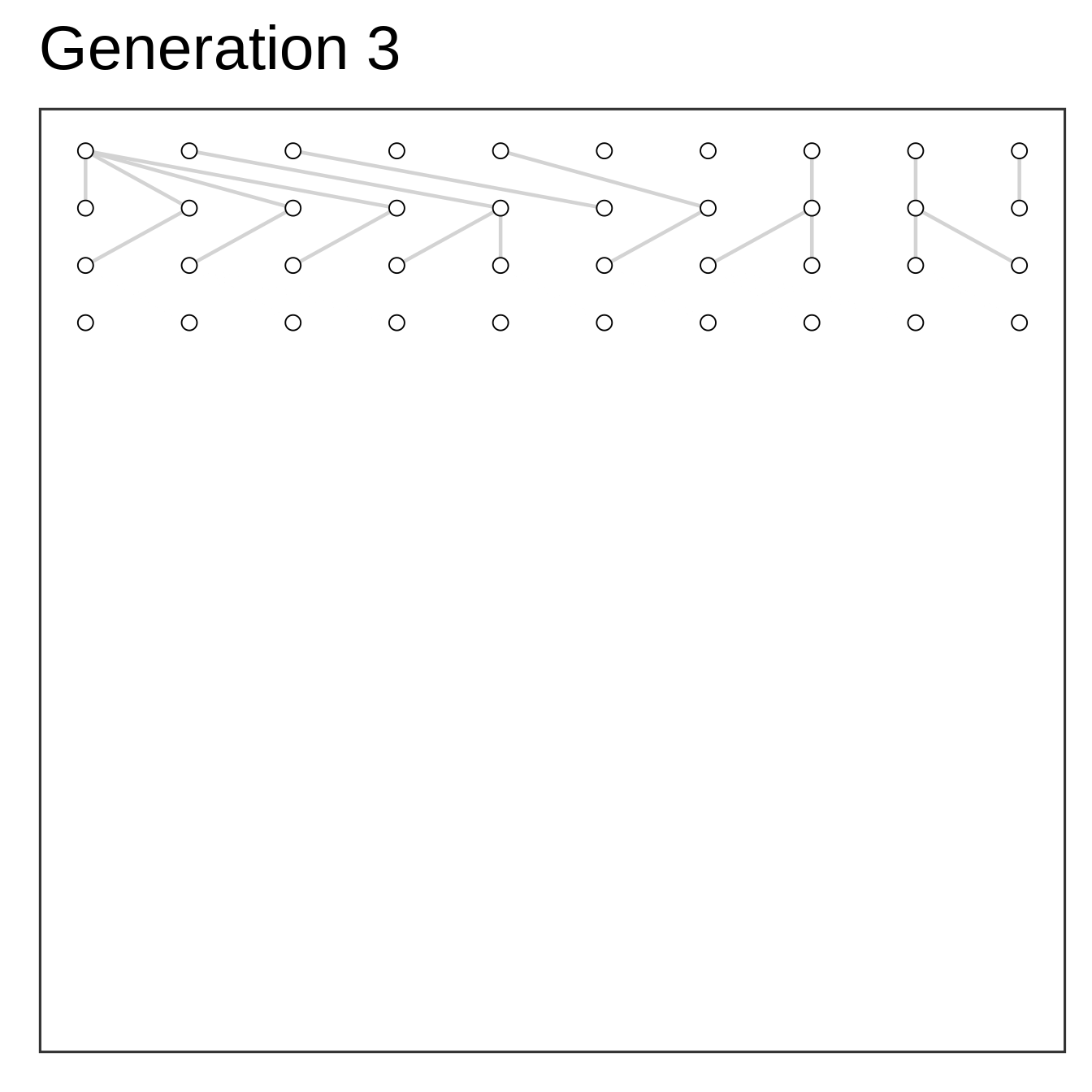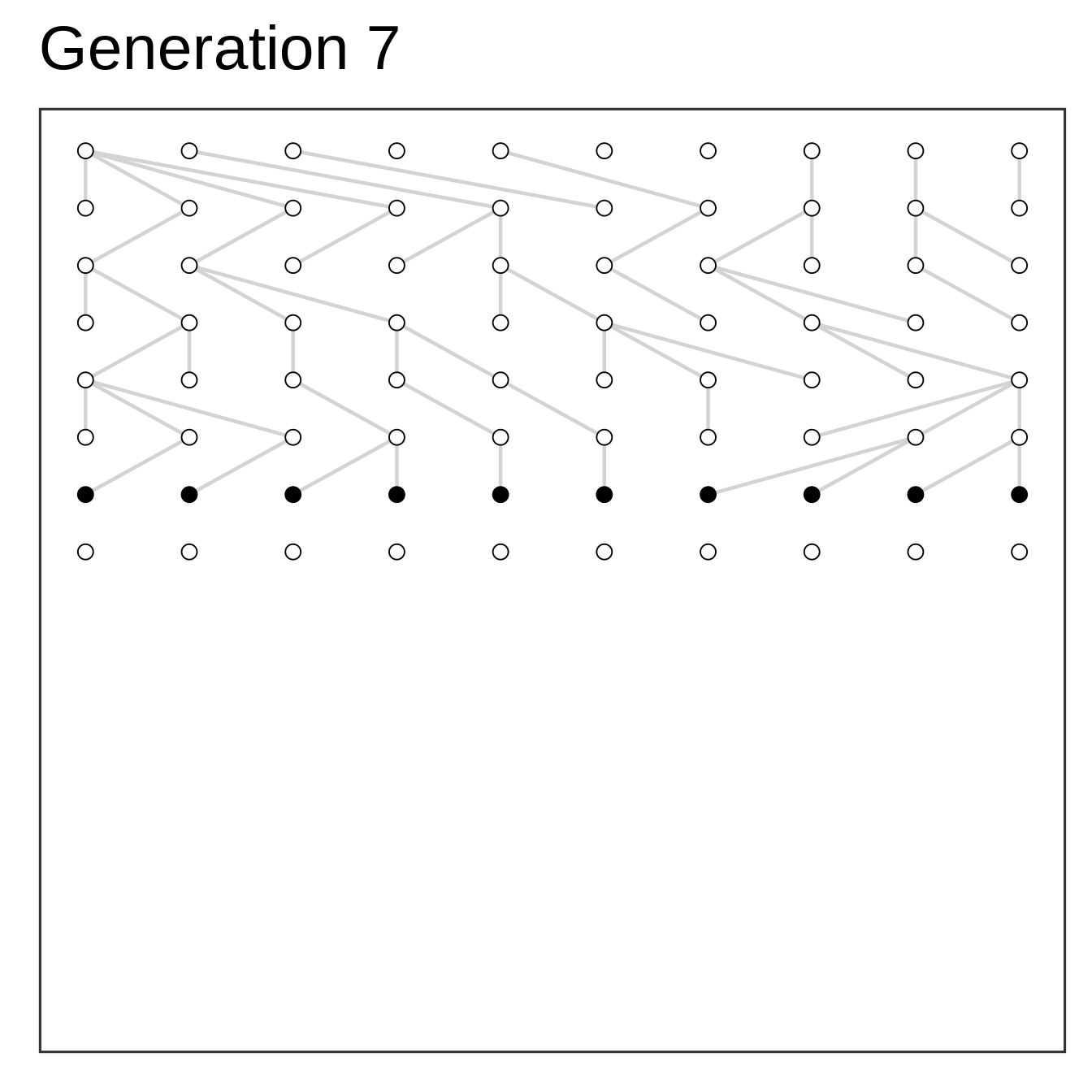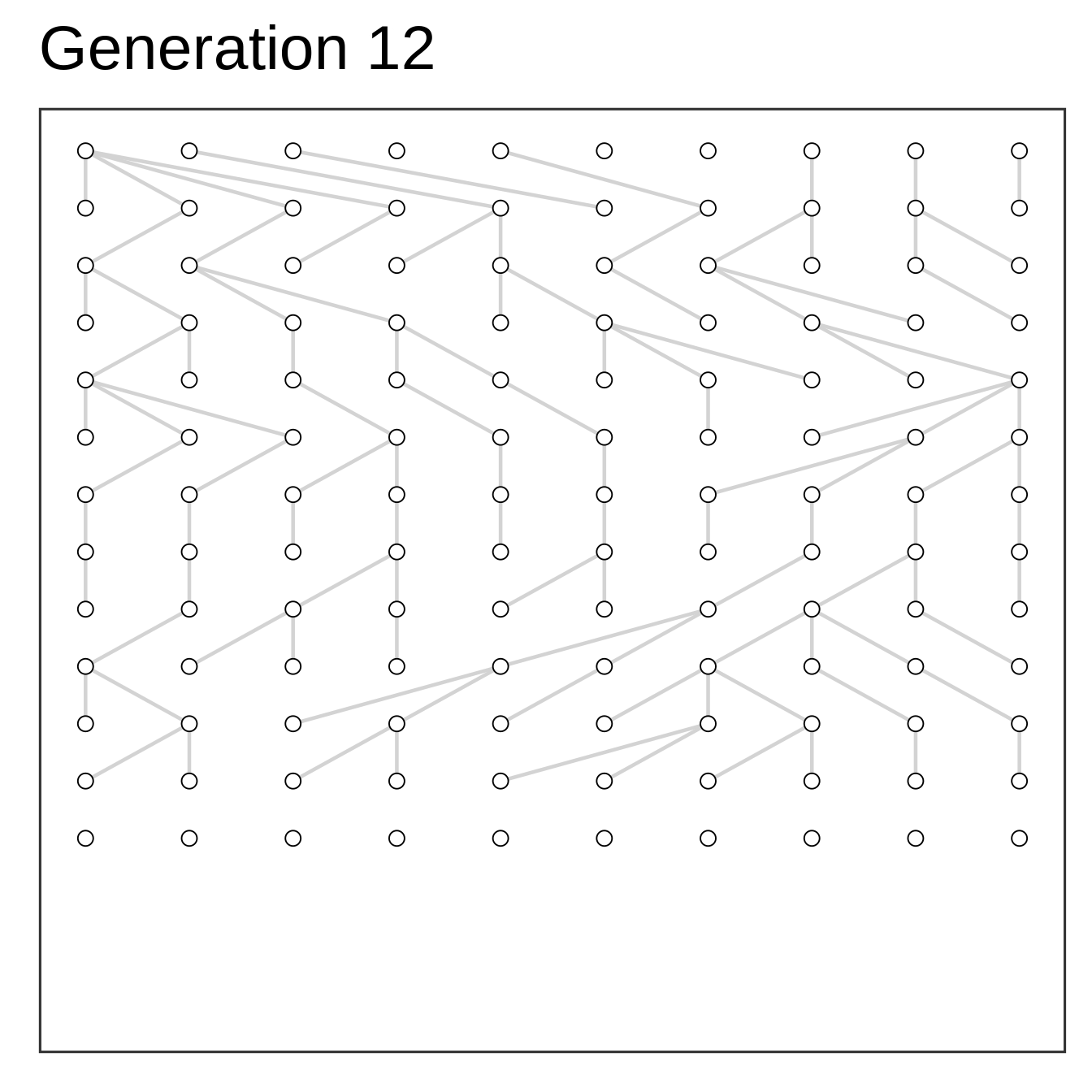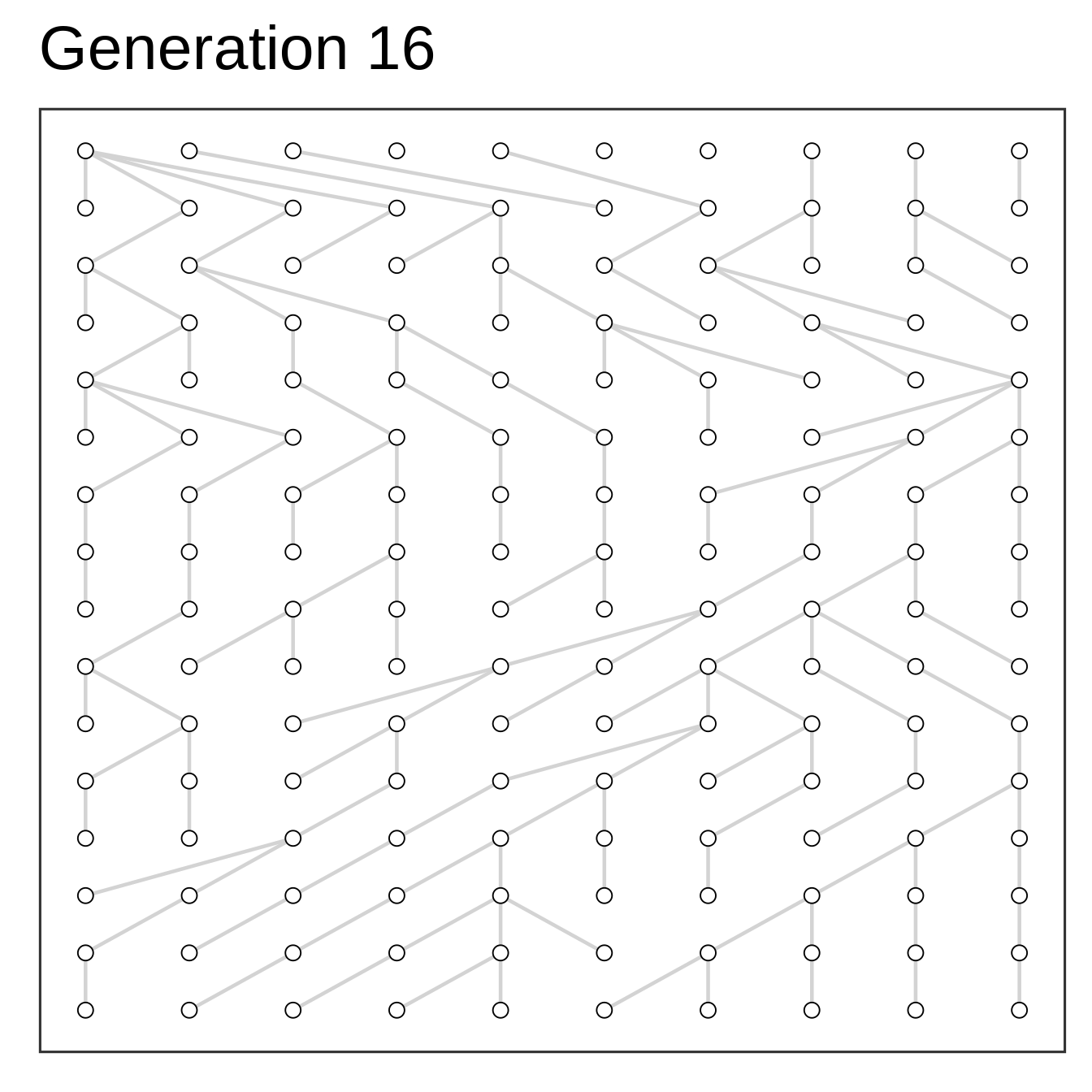
Algorithm

1. Setup starting population at time zero

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one
3. Select parents to offspring at random

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one
3. Select parents to offspring at random

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one
3. Select parents to offspring at random

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one
3. Select parents to offspring at random

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one
3. Select parents to offspring at random

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one
3. Select parents to offspring at random

Wright-Fisher model

Model of populations that describes genealogical relationships of genes (chromosomes) in a population under the following assumptions (Hein et al., 2005):

• discrete and non-overlapping generations
• haploid individuals or two subpopulations (males and females)
• constant population size
• all individuals are equally fit
• population has no geographical or social structure
• no recombination

Algorithm

1. Setup starting population at time zero
2. Add offspring (same size) at time one
3. Select parents to offspring at random

Wright-Fisher model

Figure 1: Wright-Fisher model

See https://mikeyharper.uk/animated-plots-with-r/

Wright-Fisher model

Figure 2: WF model indicating time direction from past (top) to present (bottom).

Figure 3: WF model tracing the genealogies of all extant chromosomes

Figure 4: WF model tracing the genealogies of three extant chromosomes

Observations

• most lineages are lost over time
• looking backwards in time genes eventually coalesce at a common ancestor
• looking backwards in time sampled genes can be described by a genealogy

The Wright-Fisher sampling model

Let’s formalise the sampling process of the Wright-Fisher model¹. We assume

1. a single locus in a haploid population of size 2N (or diploid of size N when random mating)
2. no mutation and selection
3. discrete generations

Each generation we sample 2N new chromosomes from the previous generation. The probability of choosing a chromosome v is 1/2N (coin flip with probability of success 1/2N). Since the trials are independent, and we perform 2N trials, the number of offspring k of a given chromosome v is binomially distributed \mathrm{Bin}(m, p), with parameters m=2N and probability of success p=\frac{1}{2N}.

We assume some familiarity with Binomial sampling. For reference, some mathematical formality follows.

Let p be the probability of heads (=1) of a coin flip, and q=1-p the probability of tails (=0). A coin flip can be modelled by a random variable (r.v.) X that follows a Bernoulli distribution, where \mathrm{Pr(}X=1\mathrm{)}=p, \mathrm{Pr(}X=0\mathrm{)}=1-p=q. One can show (e.g., with transforms such as the probability-generating function) that a binomially distributed variable Y\sim Bin(n, p) is the sum of n independent Bernoulli variables X (“Bernoulli trials”), or Y=\sum^nX. In our case, there are 2N trials, each with p=1/2N.

P(v=k) = {2N\choose k}\left( \frac{1}{2N} \right)^k \left(1 - \frac{1}{2N} \right)^{(2N - k)}

1. For a more extensive treatment, see Hermisson (2017) or Hein et al. (2005)

Properties of Wright-Fisher sampling

The expected number of offspring is one

Poisson approximation for large N

P(v=k) \approx \frac{1}{k!}e^{-k}

Prob(pick same parent) = 1/2N

Time for two sequences to coalesce \sim 1/2N

Many of the results above follow from standard results in probability theory and are provided here in brevity for reference to the interested reader. The details are not necessary to understand in detail.

Expected number of offspring

The expected value of a \mathrm{Bin}(m,p) (binomially distributed) variable with parameters m=2N and p=\frac{1}{2N} is mp, hence:

E(v) = mp = 2N\frac{1}{2N} = 1

Poisson approximation

When 2N large it holds that the probability that sequence v has k offspring is

P(v=k) \approx \frac{1}{k!}e^{-k}

Since P(v=0) = e^{-1} \approx 0.37, a fraction 0.37 of sequences lack descendants

Probability that two sequences pick same parent

Let u and v be two sequences. Pick a parent p_u of u. Then the probability that v picks the same parent is (solid lines)

P(p_u=p_v) = \frac{1}{2N}

The probability that they pick different parents is

P(p_u \neq p_v) = 1 - \frac{1}{2N}

Time for two sequences to coalescent

Time for two sequences u and v to find common ancestor distributed as (1 - \frac{1}{2N})^{j-1}\frac{1}{2N} (j-1 failures followed by success). This is the geometric distribution Ge(p), with parameter p=\frac{1}{2N}, and expected value \frac{1}{p}={2N}. That is, the expected number of generations for two sequences to find a common ancestor (i.e., coalesce) is 2N generations.

Since a large fraction of genes lack descendants, very quickly (compared to 2N) a population will descend from a small proportion of genes.

Derivation of average time to having same parent (i.e., coalescence) requires knowledge of geometric distribution. The probability that the genes find common parent j generations ago is

(1-\frac{1}{2N})^{(j-1)}\frac{1}{2N}

due to independence between generations. This is the geometric distribution Ge(p) with p=1/2N, which has expected value 1/p, i.e., 2N in this case.

Bibliography

Hein, J., Schierup, M. H., & Wiuf, C. (2005). Gene genealogies, variation and evolution: A primer in coalescent theory. Oxford University Press. https://books.google.se/books?id=CCmLNAEACAAJ

Hein, J., Schierup, M., & Wiuf, C. (2004). Gene genealogies, variation and evolution. A primer in coalescent theory. In Systematic Biology - SYST BIOL (Vol. 54).

Hermisson, J. (2017). Mathematical population genetics. https://www.mabs.at/fileadmin/user_upload/p_mabs/Lecture_Notes_2017