Selection

Per Unneberg

Selection

For a list of methods see https://methodspopgen.com/methods-to-detect-selection/

Selection and fitness

Figure 1: The life cycle used in the fundamental model of selection (Gillespie, 2004, Figure 3.2)

Much confusion exists in the literature regarding how various types of selection are defined, in particular because some of the terminology is used slightly differently within different scientific communities (Nielsen, 2005)

\begin{matrix} \mathrm{Genotype} & AA & Aa & aa \\ \mathrm{Frequency\ in\ newborns} & p^2 & 2pq & q^2\\ \mathrm{Viability} & w_{AA} & w_{Aa} & w_{aa}\\ \mathrm{Frequency\ after\ selection} & p^2w_{AA} / \bar{w} & 2pqw_{Aa} / \bar{w} & q^2w_{aa} / \bar{w} \\ \mathrm{Relative\ fitness} & 1 & 1-hs & 1-s\\ \end{matrix}

where \bar{w} = p^2w_{AA} + 2pqw_{Aa} + q^2w_{aa} is the mean fitness.

h=0	A dominant, a recessive
h=1	a dominant, A recessive
0<h<1	incomplete dominance
h<0	overdominance (heterozygote advantage)
h>1	underdominance

Notation follows Gillespie (2004), pp. 61–64.

The life cycle figure starts with newborns carrying the A allele at frequency p, like parents. To reproduce they must reach adulthood, but due to selection, the allele frequency of A may shift to p^\prime because different genotypes affect survival probabilities. This is typically summarized in genotype viabilities.

The Nielsen quote is a reminder that many different notations and parametrizations exist in the literature.

The most important equation in population genetics

p^\prime - p = \Delta_sp = \frac{pq[p(w_{AA} - w_{Aa}) + q(w_{Aa} - w_{aa})]}{p^2w_{AA} + 2pqw_{Aa} + q^2w_{aa}}

Figure 2: Allele frequency change over time for directional, balancing, and disruptive selection, for different values of p_0.

Figure 3: Rate of allele frequency change as a function of allele frequency for directional, balancing, and disruptive selection.

Given the genotype fitnesses/viabilities, we can work out the difference in allele frequency p-p^\prime between successive generations as a function of viabilities (or relative fitnesses). Equation relates allele frequency change to viabilities for different genotypes. It is instructive to study the equation and plot trajectories to gain an intuition for how allele frequencies evolve given the different selection regimes.

The left panel shows that the three modes of selection have different equilibrium points: for directional selection the favored homozygote will eventually attain 100%, balancing selection has a stable equilibrium point (attractor) for a given allelic ratio (here 25:75), and disruptive selection has an unstable equilibrium point (repeller) for a given allelic ratio.

The right panel shows the rate of change as a function of allele frequency. Note how the directionality changes at the equilibrium point for balancing and directional selection.

Selection and drift - population size matters

Figure 4: The fixation probability relative to the neutral probability of fixation (p=1/2N) under the assumption s<0.1. Red highlights region where |N_es|<0.05. Adapted from Lynch (2007), Fig. 4.2.

In red region (|N_es|<0.05) the probability of fixation is within 10% of neutral fixation.

Consequence: for any population size there exists range of selection coefficients where mutant alleles \approx neutral (effective neutrality).

Segue: note on the strength of s and the relation to N_e. For small N_e the relation will hold for higher s, meaning small populations will have difficulties purging deleterious mutations.

Even if a new mutation has, say, s=0.01, it still needs to overcome effects of drift. Only has 2% change of fixation.

In figure, we assume s<0.1, which is almost always the case (Lynch, 2007, p. 74).

(Hahn, 2019, p. 133)

Direct selection can be inferred from protein substitutions

For genes, the ratio of nonsynonymous to synonymous substitutions can tell us about protein evolution:

Synonymous substitution

Protein          L
DNA         --- CTT ---
                  *
DNA         --- CTC ---
Protein          L

Nonsynonymous substitution

Protein          L
DNA         --- CTT ---
                 *
DNA         --- CHT ---
Protein          H

\mathbf{d_N/d_S << 1}

negative (purifying) selection

\mathbf{d_N/d_S < 1}

majority nonsynonymous deleterious, some advantageous

\mathbf{d_N/d_S = 1}

neutral or mix neutral / advantageous / deleterious mutations

\mathbf{d_N/d_S > 1}

positive selection

Figure 5: d_n/d_s comparisons for human-rat orthologs. For most genes, d_n/d_s << 1 indicating purifying selection. A handful of genes (n=9) have d_n/d_s > 1.0 which could indicate positive selection.

Not all mutations fall in genes. Methods for detecting direct selection not applicable to studying selection on single mutation, or e.g., balancing. This requires looking for specific patterns of diversity surrounding locus under selection.

Segue: how do we detect selection?

Early approach: look at protein-coding sequence where nucleotide substitutions can change the amino acid (non-synonymous, and presumably non-neutral) or be silent (synonymous, assumed neutral).

Not all mutations in genes. Also want to look at single advantageous mutations, or balanced polymorphisms. Must therefore look at tell-tale signs of linked neutral variants.

Linked selection reduces diversity at neighbour loci

Figure 6: A selective sweep of an advantageous mutation (gray dot). Adapted from Charlesworth & Charlesworth (2010), Fig. 8.13

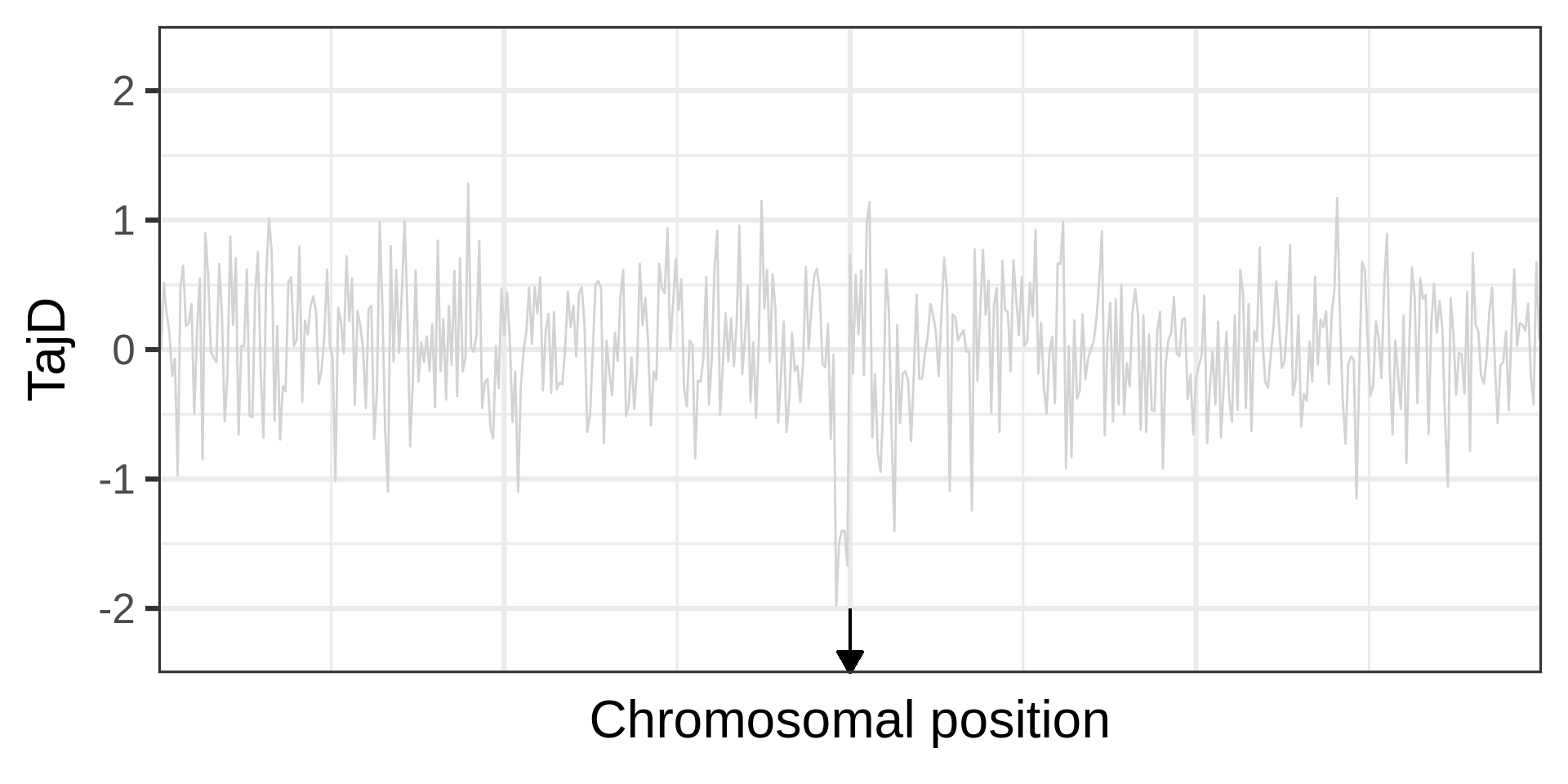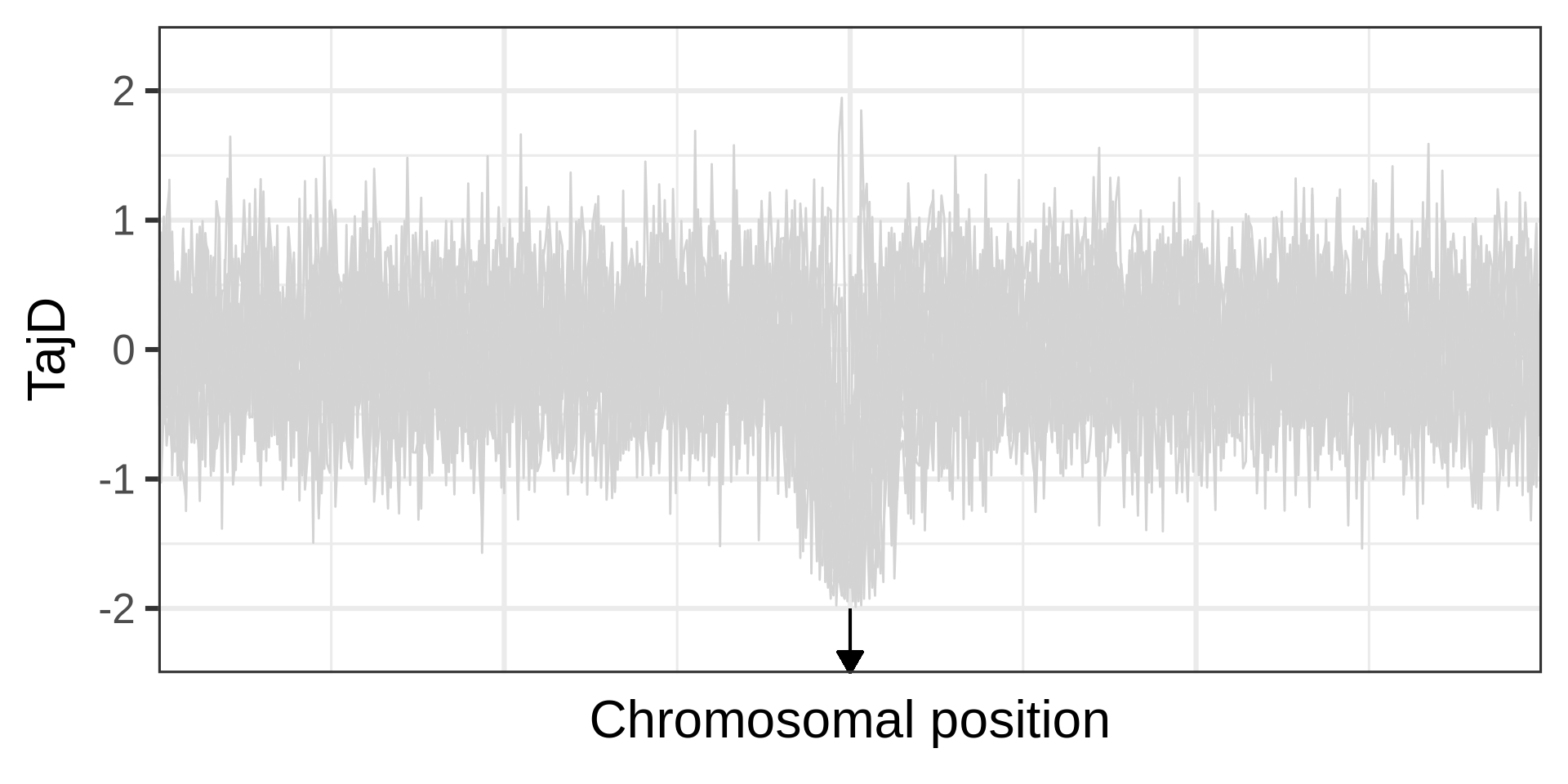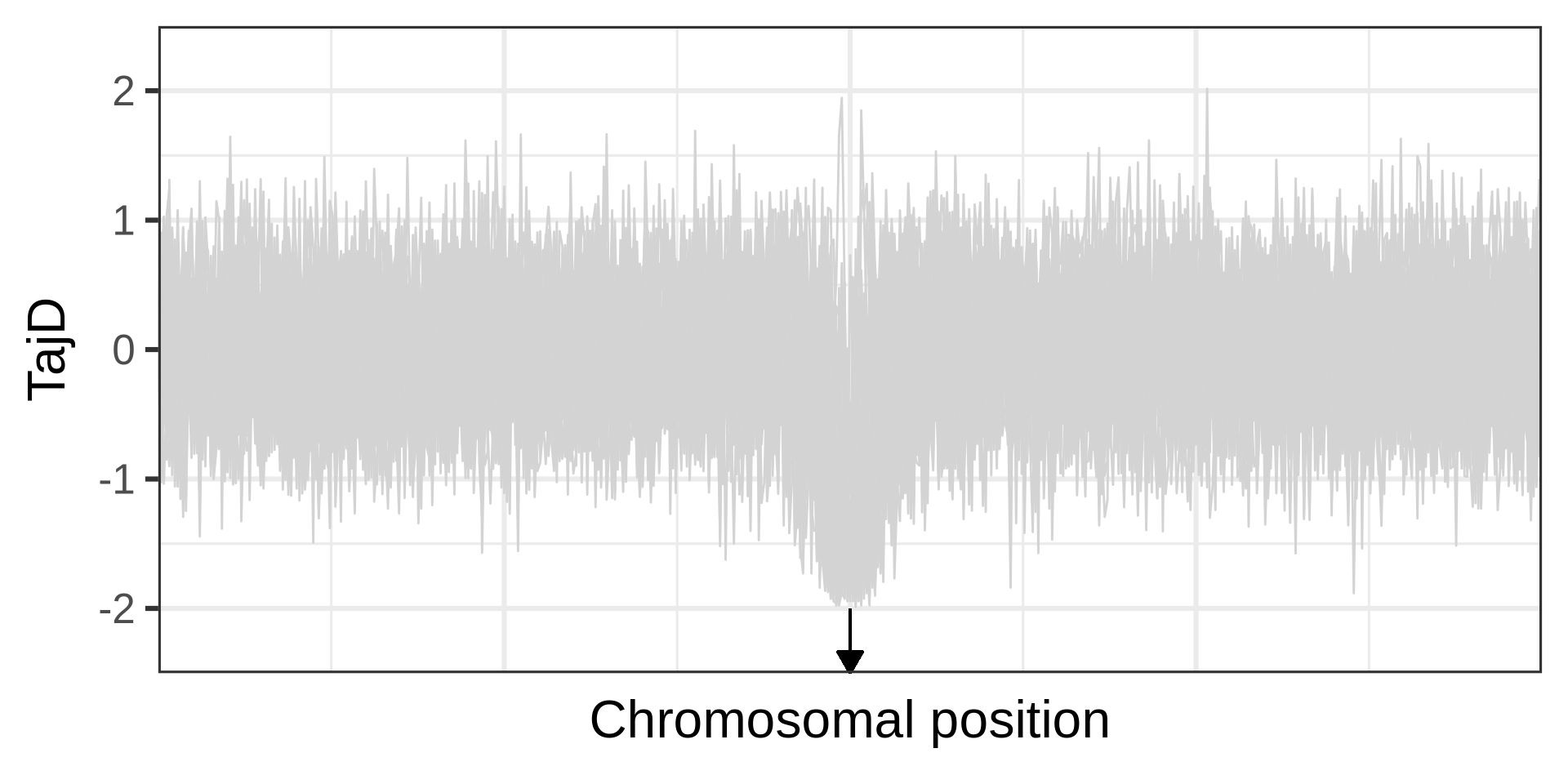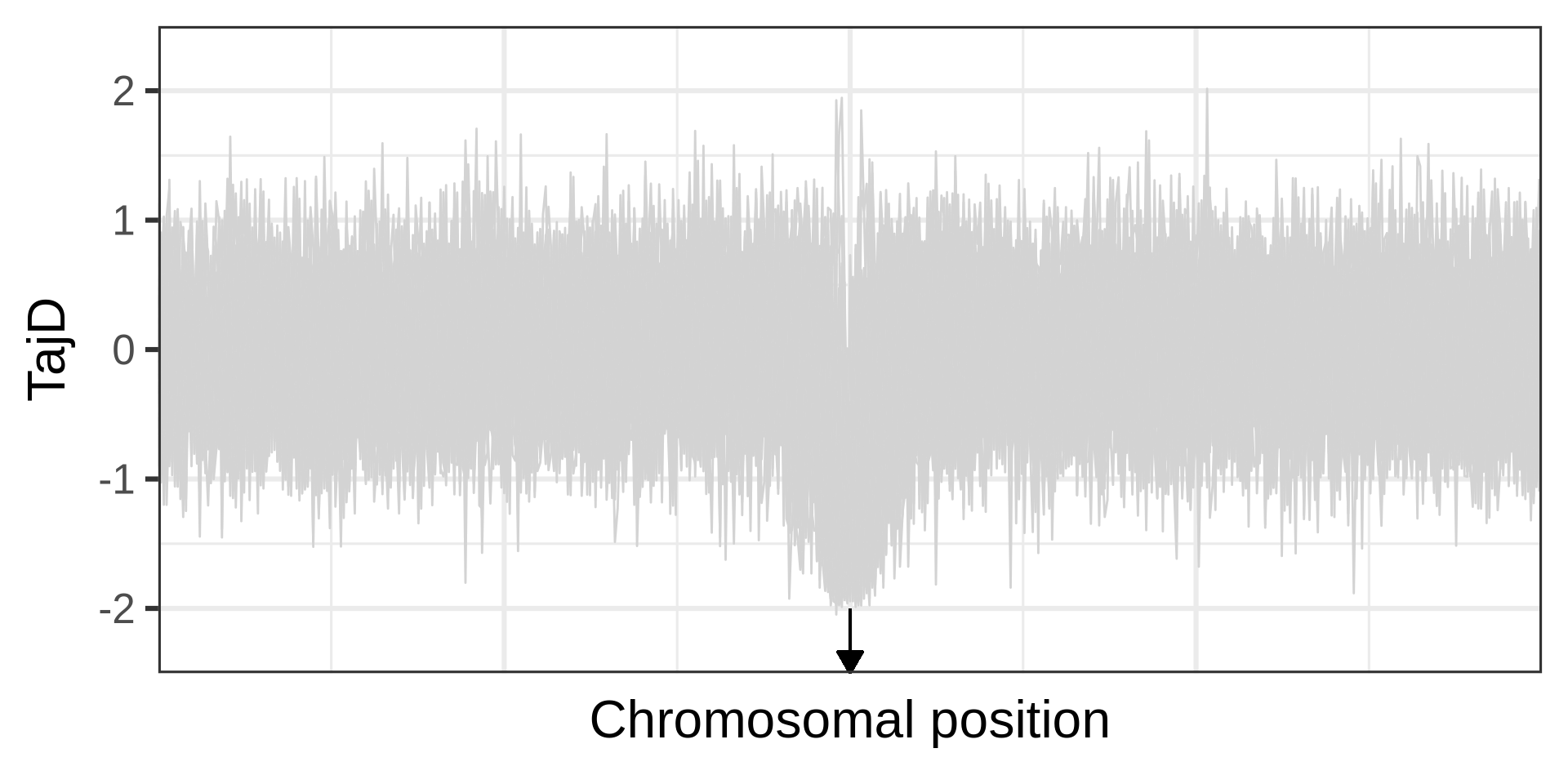
Example of a selective sweep. If a sweep completes at a locus, it will become monomorphic, as will the neighbouring sites. Mutation could reintroduce variation. Recombination could increase diversity in neighbourhood, but in a manner that depends on the distance from the locus under selection.

Alternatives to direct selection tests are those that look at linked selection. In essence, we look for characteristic patterns in the vicinity of a selected locus. A sweep leads to the selected site and neigbouring sites being monomorphic (and therefore invisible to tests based on direct selection). Without recombination, mutation could reintroduce variation. In the presence of recombination, the effect of reduced diversity will be dependent on distance from the locus under selection.

Note here that every sequence can be treated as an allele, such that we in essence are looking multi- and not a bi-allelic locus.

The effect of a selective sweep on diversity

pgip-slim --seed 42 -n 1000 -r 1e-6 -m 1e-7 --threads 12 recipes/slim/selective_sweep.slim -l 1000000 --outdir results/slim
pgip-tsstat results/slim/slim*.trees -n 10 --seed 31 -s pi -s S -s TajD -w 500 --threads 10 | gzip -v - > results/slim/selective_sweep.w500.csv.gz

Figure 7: The effect of a selective sweep on diversity. The arrow points to the site under selection. The y-axis shows Tajima’s D which is proportional to the difference between two measures of diversity, nucleotide diversity \pi and Watterson’s \theta_W.

Simulation: N=1e4, mu=5e-8, pi=4Nmu=0.004, seek S=a*pi=0.01, so a=S/pi which gives n. One needs to ramp up recombination rate to see the dip in TajD clearly.

The effect of a selective sweep on diversity

pgip-slim --seed 42 -n 1000 -r 1e-6 -m 1e-7 --threads 12 recipes/slim/selective_sweep.slim -l 1000000 --outdir results/slim
pgip-tsstat results/slim/slim*.trees -n 10 --seed 31 -s pi -s S -s TajD -w 500 --threads 10 | gzip -v - > results/slim/selective_sweep.w500.csv.gz

Figure 8: The effect of a selective sweep on diversity. The arrow points to the site under selection. The y-axis shows Tajima’s D which is proportional to the difference between two measures of diversity, nucleotide diversity \pi and Watterson’s \theta_W.

Important: individual runs show a lot of stochasticity, but the signal is clear for the mean.

The effect of a selective sweep on diversity

Figure 9: The effect of a selective sweep on diversity. The figure shows the mean of 1000 simulations with the selected locus indicated with an arrow.

cf Nielsen (2005). Not clear how scaling of statistics to have mean=1 is done.

The phases of a selective sweep

Figure 10: Time goes from left to right. As sweep progresses, tree topology changes. Adapted from Hahn (2019), Figure 8.1

Amount of diversity depends on fixation time. A neutral locus fixes in 4N_e generations; for s=0.0001, it takes approximately 0.29N_e generations.

Selections changes the genealogy (different topology, shorter branches), an aspect used in many linkage-based tests for selection.

A selective sweep changes the genealogy (shorter branches, different topology) compared to the neutral case, a fact that can be utilised in linkage-based tests for selection.

Note that the amount of variation surrounding a sweep depends heavily on the rate of the sweep. (Hahn, 2019, p. 167) points out that an advantageous allele with s=0.0001 will take approximately 0.29N_e generations to fix (compared to 4N_e generations for a neutral locus)

Linked selection may constrain levels of diversity

Figure 11: Hitchhiking (left) versus background selection (right).

Hitchhiking

• alleles linked to locus under selection “hitchhike” to high frequencies (Smith & Haigh, 1974)
• evidence: positive correlation between putative neutral diversity and recombination (Corbett-Detig et al., 2015)

Background selection

• loci linked to a deleterious locus will be purged from population and thus reduce diversity (Charlesworth et al., 1993)
• similar patterns to hitchhiking

Linked selection has been proposed as solution to the low range of diversity seen between species with orders of magnitude ranges in census population sizes.

Summary

We have looked at the Wright-Fisher model as a model of populations and genealogies

Genetic drift moves allele frequencies up and down at random and removes variation at rate \propto 1/2N

Mutation reintroduces variation. The Neutral theory posits most mutations are neutral and dynamics follow mutation drift equilibrium.

Methods to detect selection are based on direct selection or studying patterns of variation caused by linked selection.

Bibliography

Charlesworth, B., & Charlesworth, D. (2010). Elements of Evolutionary Genetics. Roberts and Company Publishers.

Charlesworth, B., Morgan, M. T., & Charlesworth, D. (1993). The Effect of Deleterious Mutations on Neutral Molecular Variation. Genetics, 134(4), 1289–1303.

Corbett-Detig, R. B., Hartl, D. L., & Sackton, T. B. (2015). Natural Selection Constrains Neutral Diversity across A Wide Range of Species. PLOS Biology, 13(4), e1002112. https://doi.org/10.1371/journal.pbio.1002112

Gillespie, J. H. (2004). Population Genetics: A Concise Guide (2nd edition). Johns Hopkins University Press.

Hahn, M. (2019). Molecular Population Genetics (First). Oxford University Press.

Lynch, M. (2007). The origins of genome architecture. Sinauer Associates.

Nielsen, R. (2005). Molecular Signatures of Natural Selection. Annual Review of Genetics, 39(1), 197–218. https://doi.org/10.1146/annurev.genet.39.073003.112420

Smith, J. M., & Haigh, J. (1974). The hitch-hiking effect of a favourable gene. Genetics Research, 23(1), 23–35. https://doi.org/10.1017/S0016672300014634