Descriptive statistics

Introduction

Two main types of statistics

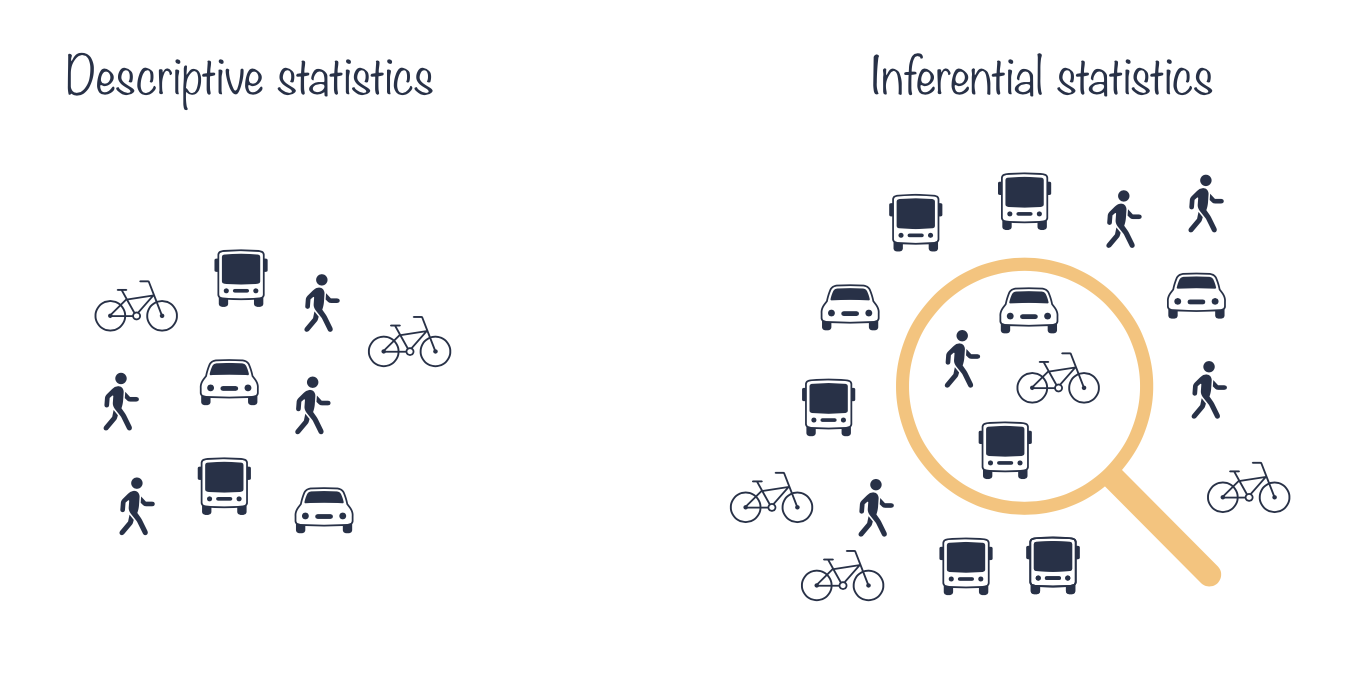
• Descriptive statistics describes and summarizes the data.
• It can be contrasted with inferential statistics that uses a sample of data to make inferences about the population that the sample of data is drawn from.

Introduction

Descriptive statistics

Descriptive statistics is a term describing simple analyses of data to help getting to know the data by:

• describing the data
• showing & visualizing the data
• summarizing the data

Beyond getting to know the data descriptive statistics is used to:

• uncover potential patterns in the data, incl. outliers
• guide down-stream analysis

Data types

numerical & categorical data types

One of the first thing we tend to notice about the data is the data type. We differentiate between categorical (qualitative) and numerical (quantitative) data types.

flowchart LR
  A(Data types) --> B(Categorical)
  A --> C(Numerical)

Depending on the data type we use different methods to describe, summarize and visualize the data. Beyond descriptive statistics, we even use different methods to analyse the data.

Data types

Categorical data

Categorical data can be further divided into:

flowchart LR
  A(Data types) --> B(Categorical)
  A --> C(Numerical)
  B(Categorical) --> D(Nominal i.e. named)
  B --> E(Ordinal i.e. named and ordered)

• Nominal: named, categories are mutually exclusive and unordered
  • e.g.dead/alive, healthy/sick, WT/mutant, A/B/AB/O, male/female, red/green/blue

• Ordinal: named and ordered, categories are mutually exclusive and ordered
  • e.g. pain (weak, moderate, severe), very young/young/middle age/old/very old, grade I, II, III, IV

Data types

Numerical data

Numerical data can be further divided into:

flowchart LR
  A(Data types) --> B(Categorical)
  A(Data types) --> C(Numerical)
  C(Numerical) --> D(Discrete i.e. finite or countable infinite values)
  C(Numerical) --> E(Continuous i.e. infinitely many uncountable values)

• Discrete: finite or countable infinite values
  • days sick last year, number of cells, number of reads

• Continuous: infinitely many uncountable values
  • e.g. height, weight, concentration

Diabetes data set

Example data set

• 403 participants were interviewed in a study to understand the prevalence of obesity, diabetes, and other cardiovascular risk factors in central Virginia
• The data is available as part of faraway package.

Abbreviation	Description
id	Subject ID
chol	Total Cholesterol [mg/dL]
stab.glu	Stabilize Glucose [mg/dL]
hdl	High Density Lipoprotein [mg/dL]
ratio	Cholesterol / HDL Ratio
glyhb	Glycosolated Hemoglobin [%]
location	County: Buckingham or Louisa
age	age [years]
gender	gender
height	height [in]
weight	weight [lb]
frame	frame: small, medium or large
bp.1s	First Systolic Blood Pressure
bp.1d	First Diastolic Blood Pressure
bp.2s	Second Systolic Blood Pressure
bp.2d	Second Diastolic Blood Pressure
waist	waist [in]
hip	hip [in]
time.ppn	Postprandial Time [min] when labs were drawn

Diabetes data set

Example data set

• Glycosolated hemoglobin \(>7.0\) is usually taken as a positive diagnosis of diabetes, so we can add variable diabetic (yes/no) reflecting this information.
• We can calculate BMI as \(BMI = 703 \times (weight \; [lb] \; / (height \;[in])^2)\) and define obesity as \(BMI \ge 30\) storing this information in obese variable (yes/no).
• First few observations omitting samples with missing data (complete case analysis) are shown on the right.

Rows: 6
Columns: 22
$ id       <int> 1002, 1011, 1016, 1024, 1036, 1252
$ chol     <int> 228, 195, 177, 242, 213, 186
$ stab.glu <int> 92, 92, 87, 82, 83, 97
$ hdl      <int> 37, 41, 49, 54, 47, 50
$ ratio    <dbl> 6.2, 4.8, 3.6, 4.5, 4.5, 3.7
$ glyhb    <dbl> 4.64, 4.84, 4.84, 4.77, 3.41, 6.49
$ location <fct> Buckingham, Buckingham, Buckingham, Louisa, Louisa, Buckingham
$ age      <int> 58, 30, 45, 60, 33, 70
$ gender   <fct> female, male, male, female, female, male
$ height   <dbl> 1.55, 1.75, 1.75, 1.65, 1.65, 1.70
$ weight   <dbl> 115.20, 85.95, 74.70, 70.20, 70.65, 80.10
$ frame    <fct> large, medium, large, medium, medium, large
$ bp.1s    <int> 190, 161, 160, 130, 130, 148
$ bp.1d    <int> 92, 112, 80, 90, 90, 88
$ bp.2s    <int> 185, 161, 128, 130, 120, 148
$ bp.2d    <int> 92, 112, 86, 90, 96, 84
$ waist    <dbl> 1.2446, 1.1684, 0.8636, 0.9906, 0.9398, 1.0668
$ hip      <int> 57, 49, 40, 45, 41, 41
$ time.ppn <int> 180, 720, 300, 300, 240, 1020
$ BMI      <dbl> 47.95, 28.07, 24.39, 25.79, 25.95, 27.72
$ obese    <fct> Yes, No, No, No, No, No
$ diabetic <fct> No, No, No, No, No, No

Categorical data

Summarizing categorical data

flowchart TD
  A(Categorical data) --> B(Numerical summary)
  B(Numerical summary) --> D(Table of frequencies <br/> Proportions <br/> Percentages <br/> ...)
  A(Categorical data) --> C(Graphical summary)
  C(Graphical summary) --> E(Bar chart <br/> Pie chart <br/> Mosaic plot <br/> ...)

Figure 1: Main method of summarizing categorical data types. Numerical summaries include frequency, summary and contingency tables together with listing proportions and percentages. Graphical summaries include bar charts, pie charts and mosaic plots.

Categorical data

Summarizing categorical data

Let’s preview again first few measurements of diabetes data set focusing on gender and obese variables.

Table 1: Diabetes data: first few observations of gender and obesity status.

id	gender	obese
1002	female	Yes
1011	male	No
1016	male	No
1024	female	No
1036	female	No
1252	male	No
1253	male	Yes
1256	female	Yes
1271	female	No
1285	male	No

• Information about gender and obese status falls under categorical data type.
• To summarize these variables we can ask questions such as:
  • how many participants we have in each category?
  • what are the percentages or proportions in each category?
• We can also visualize these descriptive statistics in a bar chart of a pie chart.

Categorical data

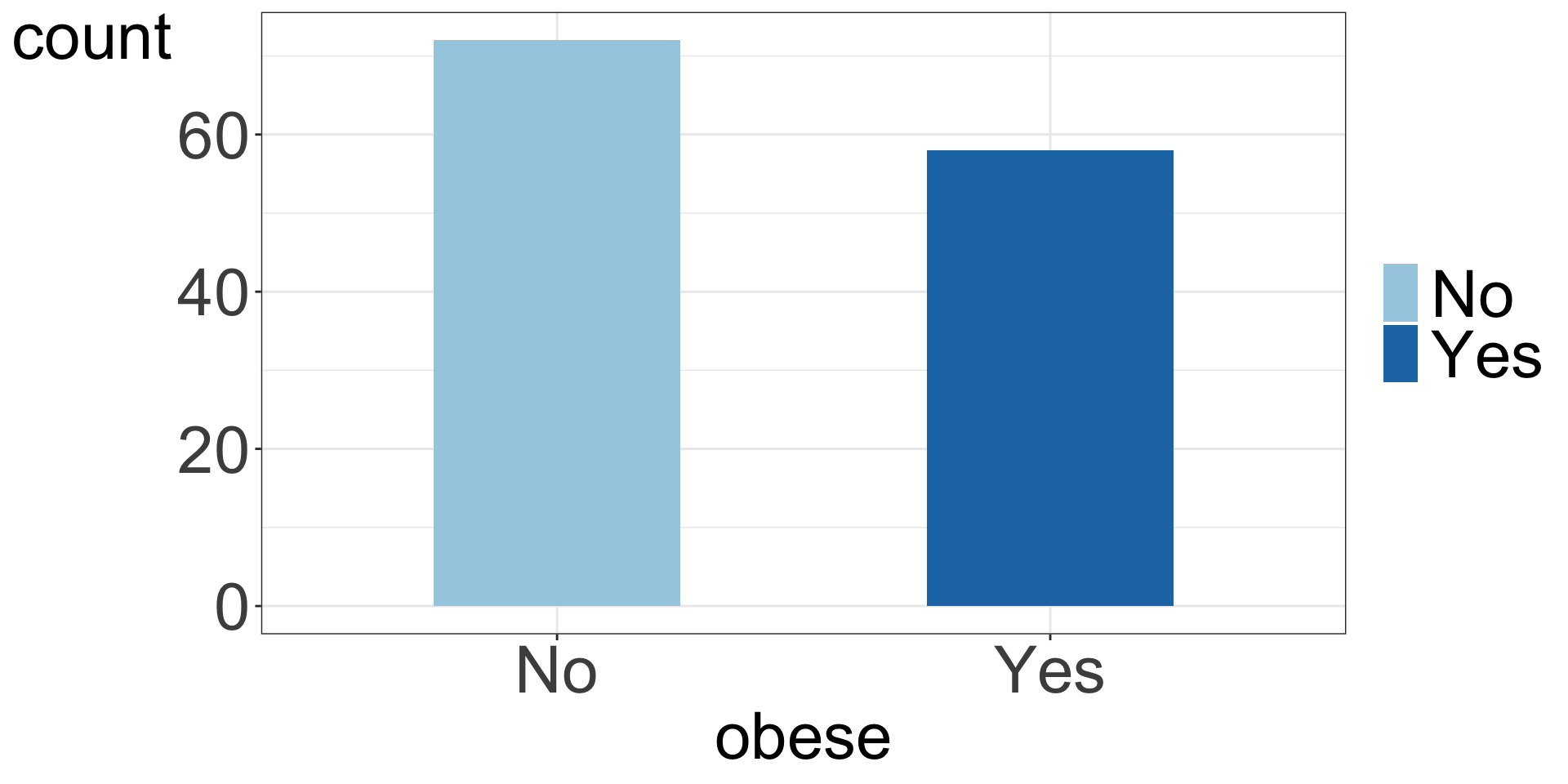
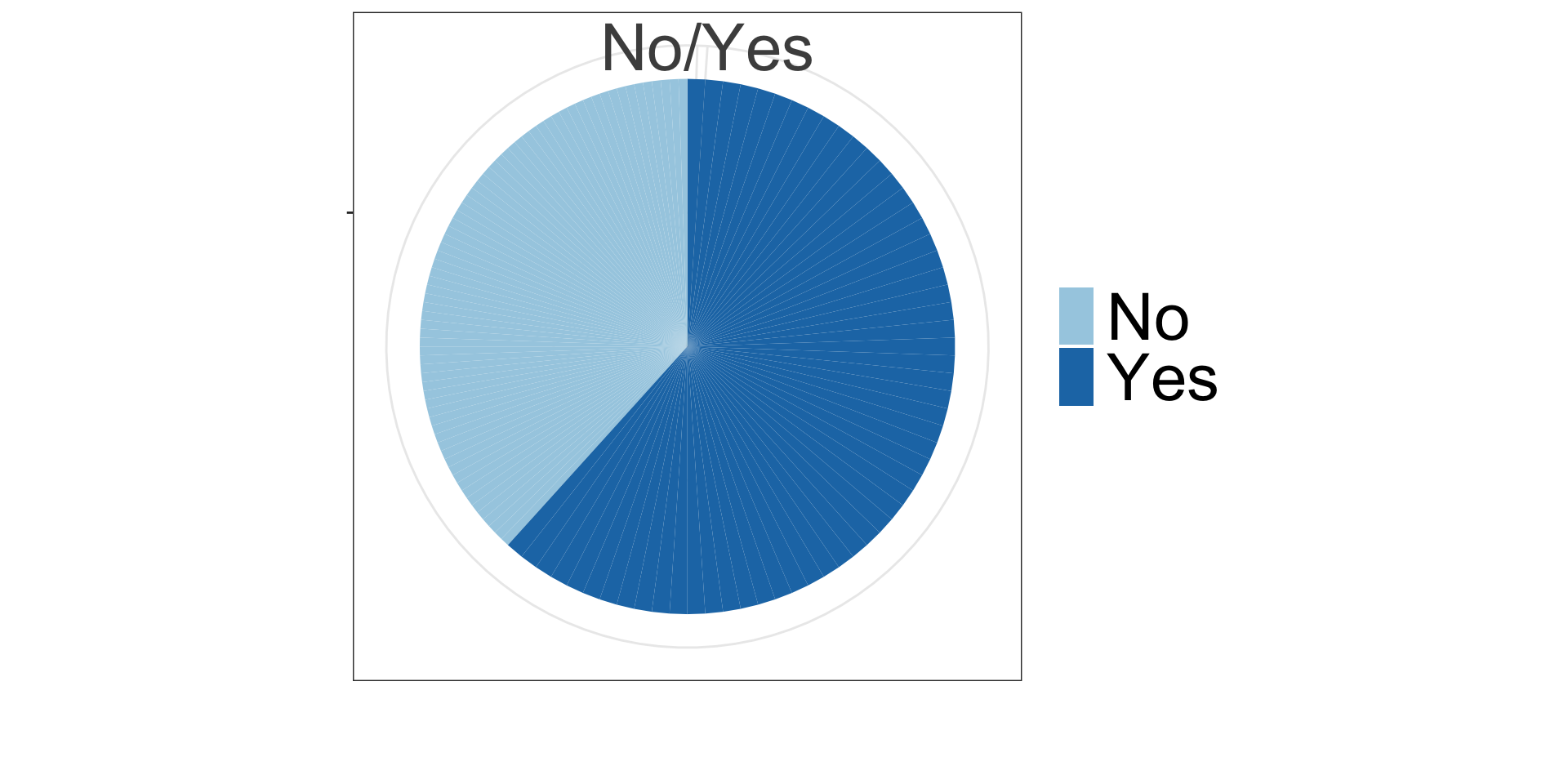
Frequency table. Bar and pie charts.

Frequency table shows the number, percentages and proportions of study participants with BMI \(\ge\) 30 and with BMI < 30.

obese	n	percent (%)	proportion
No	72	55.4	0.6
Yes	58	44.6	0.4

Bar chart

Pie chart

Categorical data

Summary and contingency table: 2 categorical variables

When we are interested in how one categorical variable is related to another categorical variable, we can use a summary table. For instance, we can look at the relationship between obesity (yes/no) and diabetes (yes/no).

obese	Total	Diabetic	Diabetic (%)
No	72	39	54.17
Yes	58	18	31.03

Contingency table, sometimes called two-way frequency table, shows the multivariate frequency distribution of variables.

	Non-diabetic	Diabetic	Sum
Non-obese	57	15	72
Obese	43	15	58
Sum	100	30	130

Categorical data

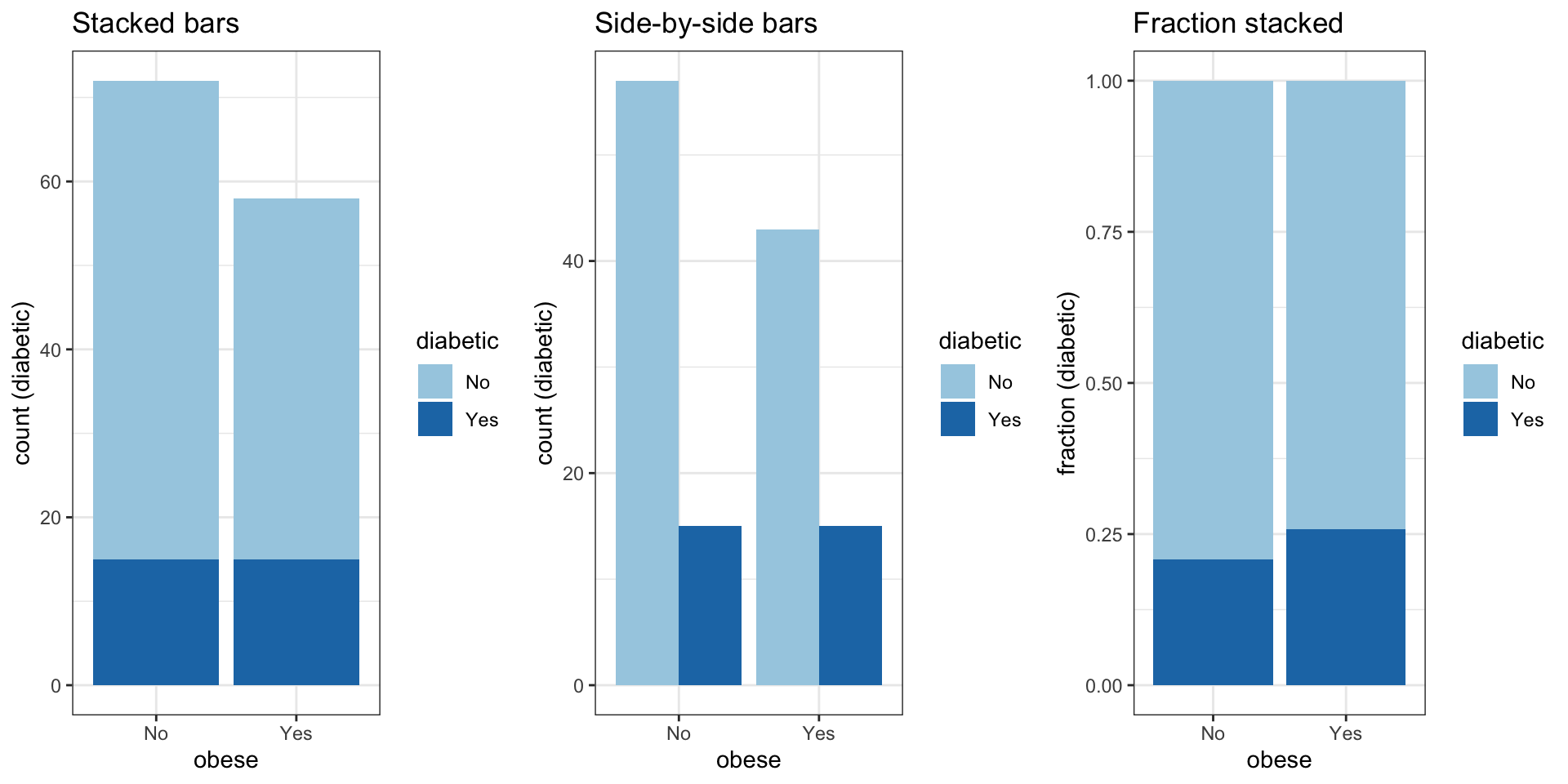
Bar charts: 2 categorical variables

Bar charts can be used to visualize two and more categorical variables, e.g. by using stacking, side-by-side bars or colors.

Figure 2: Bar charts visualizing two caterogircal variables using stacking, side-by-side bars and colours.

Categorical data

Mosaic plot

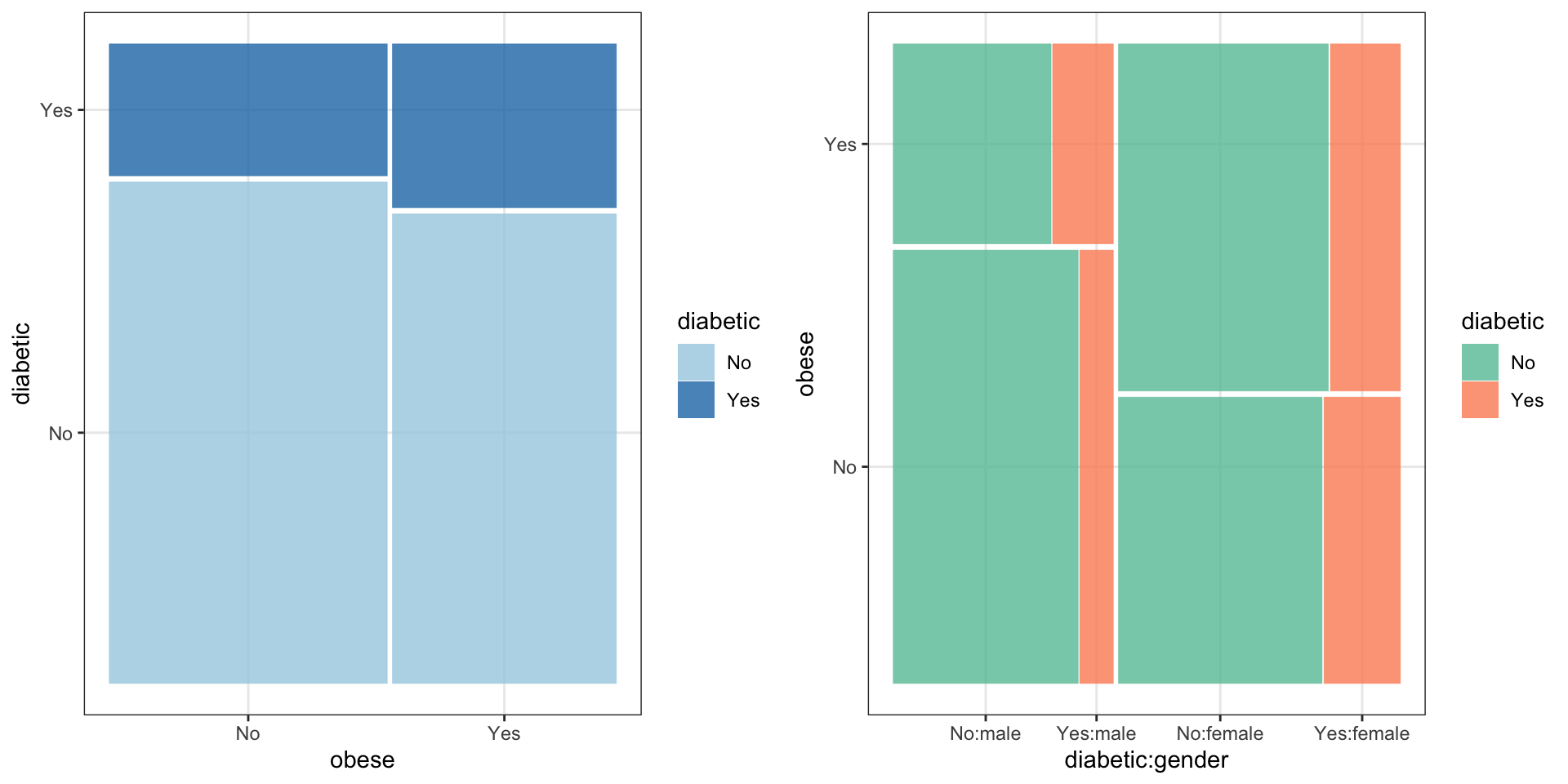
Figure 3: Mosaic plots display contigency tables, here of obesity and diabetic status among study pariticipants (left) and colour-coded by gender (right).

Numerical data

Summarizing numerical data

Numerical data can be visualized and summarized in many ways. Common plots include histograms, density plots and scatter plots. Summary statistics include measures of location such as mode and median and measures of spread such as variance or median absolute deviation. It is also common to visualize summary statistics, e.g. on box plot.

flowchart TD
  A(Numerical data) --> B(Numerical summary)
  A(Numerical data) --> C(Graphical summary)
  B(Numerical summary) --> D(Measures of location <br/> e.g. mode, average, median)
  B --> E(Measures of spread <br/> e.g. quartiles, variance, standard deviation)
  C(Graphical summary) --> F(Histogram <br/> Density plot <br/> Box plot <br/> ...)

Numerical data

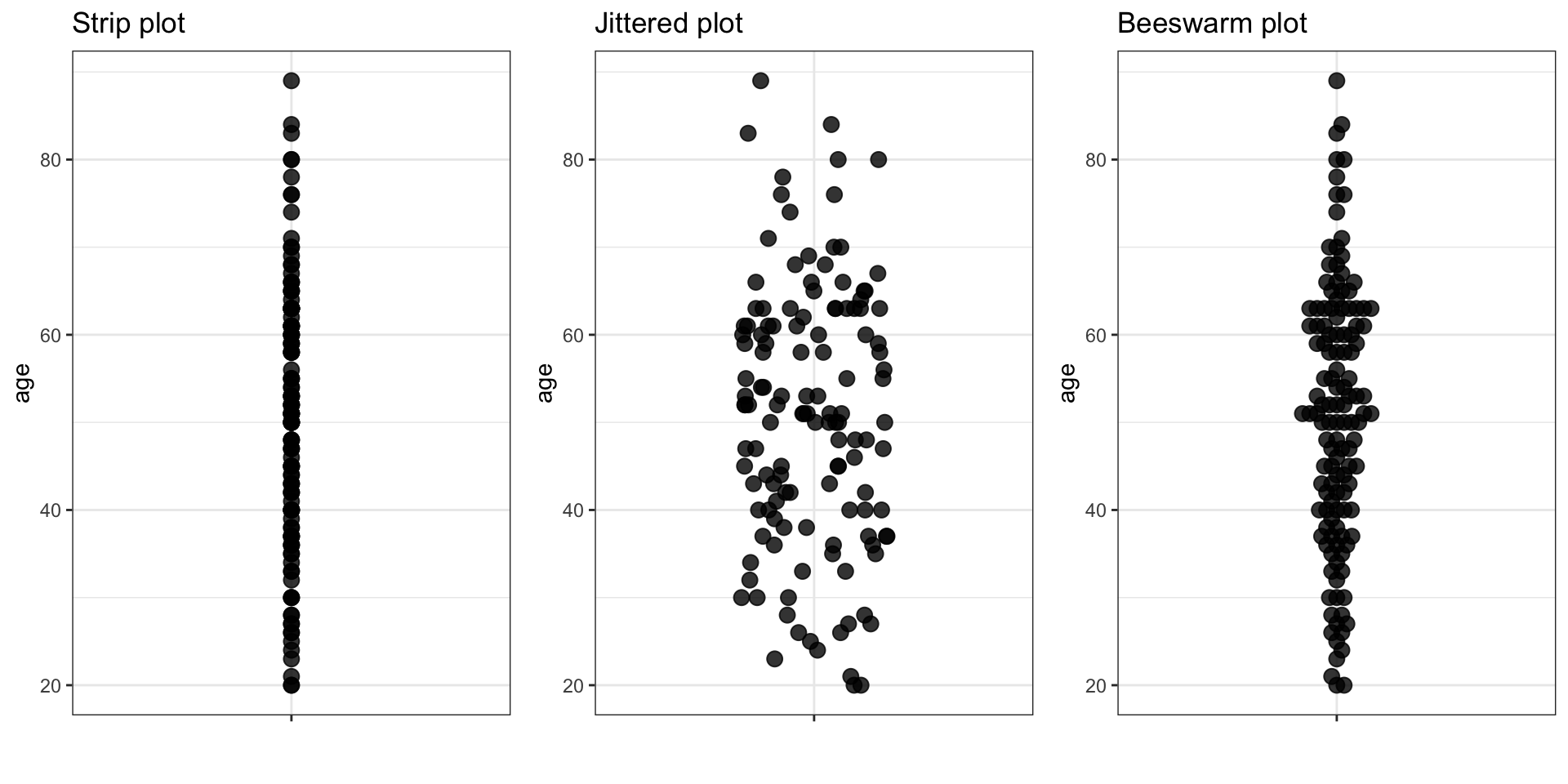
Strip plot, Jittered strip plot & Beeswarm plot

If it is technically feasible, it is recommended to visually assess all measurements on a plot.

Figure 4: Strip plot, jittered strip plot and beeswarm plot showing all measurmentes of age variable (complete cases analysis).

Numerical data

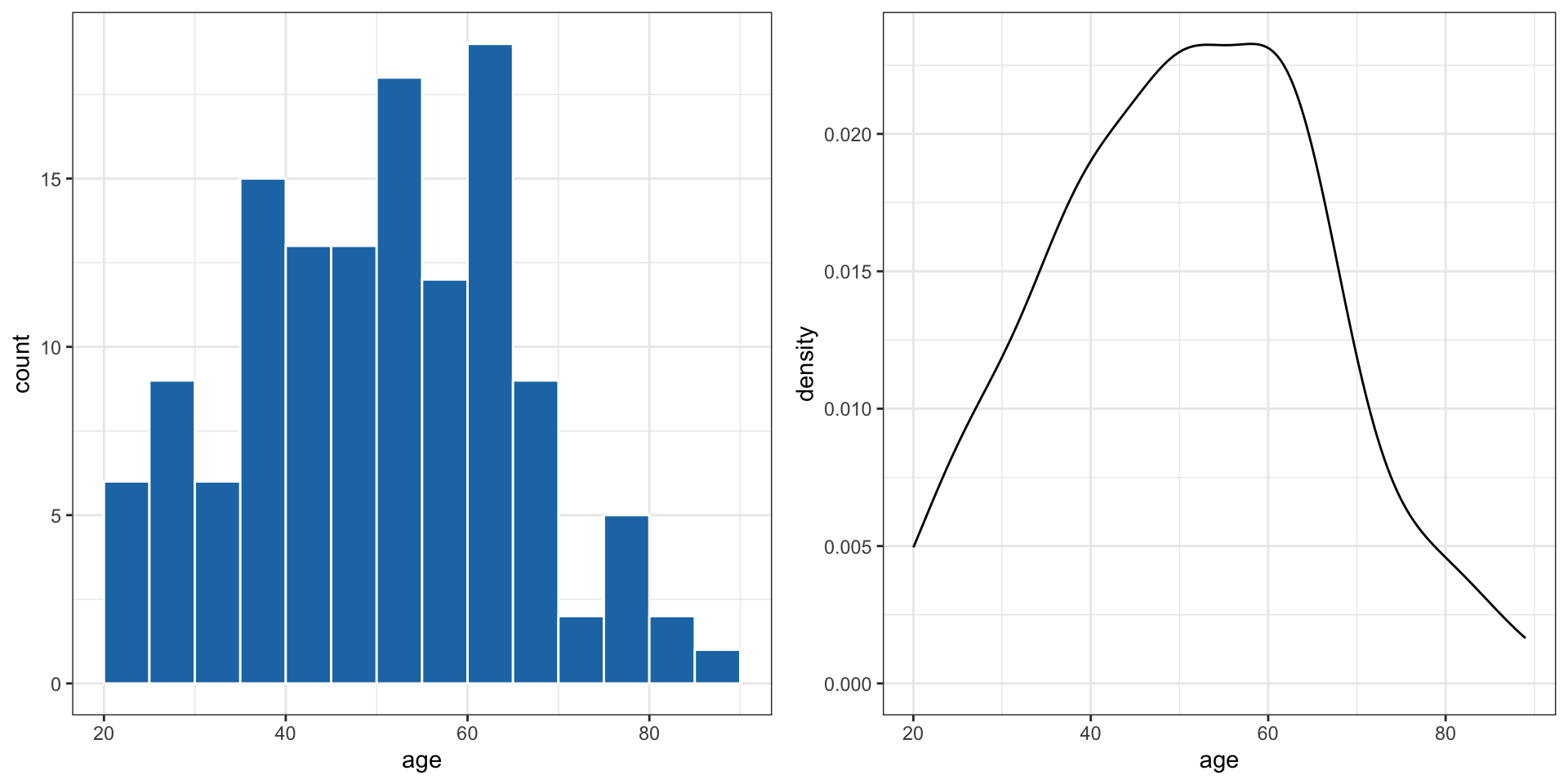
Histogram & density plot

A histogram bins the data and counts the number of observations that fall into each bin. A density plot is like a smoothed histogram where the total area under the curve is set to 1. A density plot is an approximation of a distribution.

Figure 5: Histogram of the age measurmentes exluding missing data (left) and a corresponding density plot (right).

Numerical data

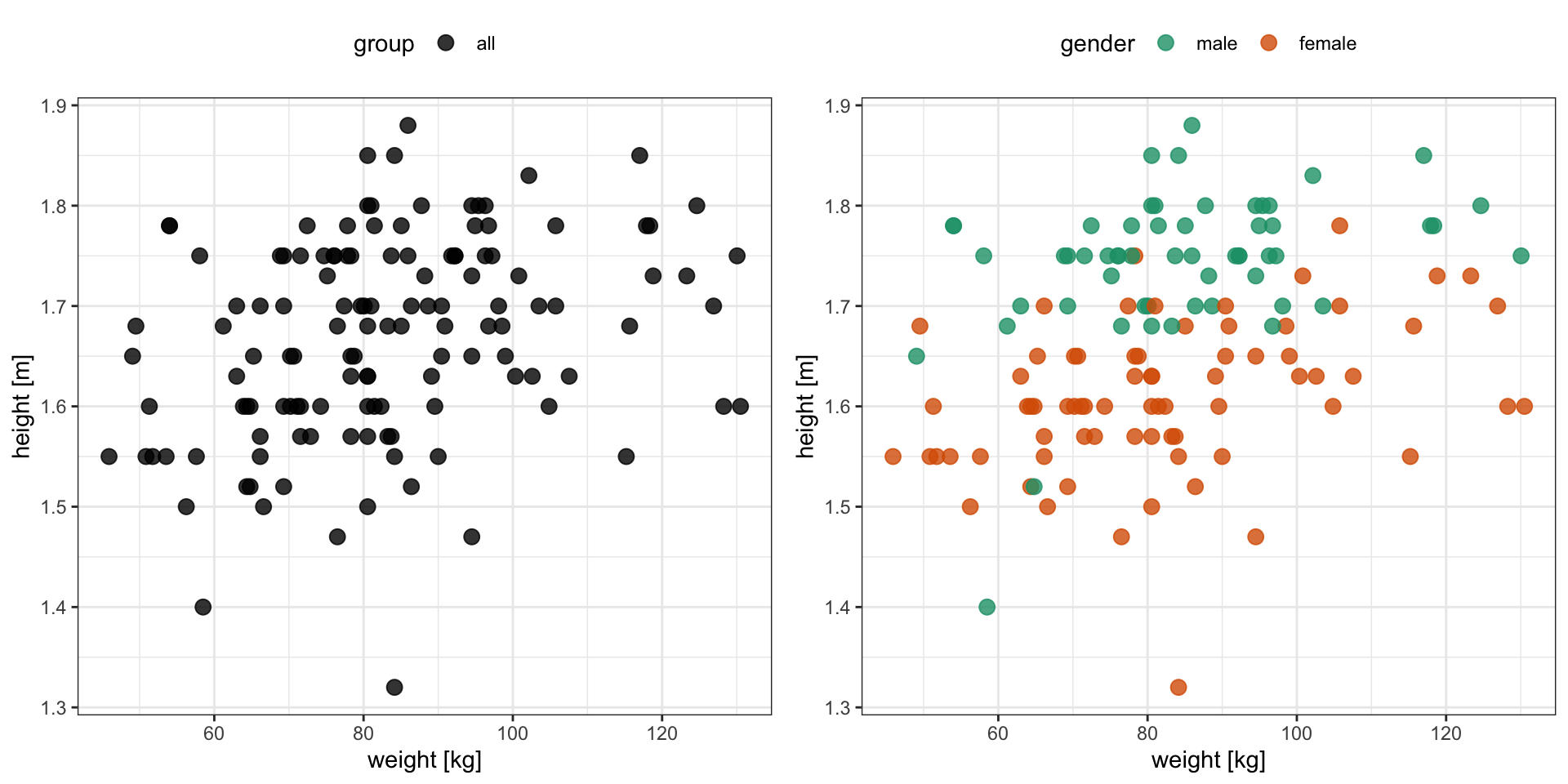
Scatter plot: 2 numerical variables

Scatter plots are useful when studying a relationship (association) between two numerical variables.

Figure 6: Scatter plot showing relationship between weight and height (left) and including color-coding by gender (right).

Numerical data

Scatter plot: 2 numerical variables cont.

Sometimes, it is useful to connect the observations in the order in which they appear, e.g. when analyzing time series data. The diabetes data set does not contain any measurements over time but we can simulate some BMI values over time for demonstration purposes.

Figure 7: Scatter plot for simulated over 12 weeks BMI values for 10 participants in a mock up study (left) and colour-coded by a study group.

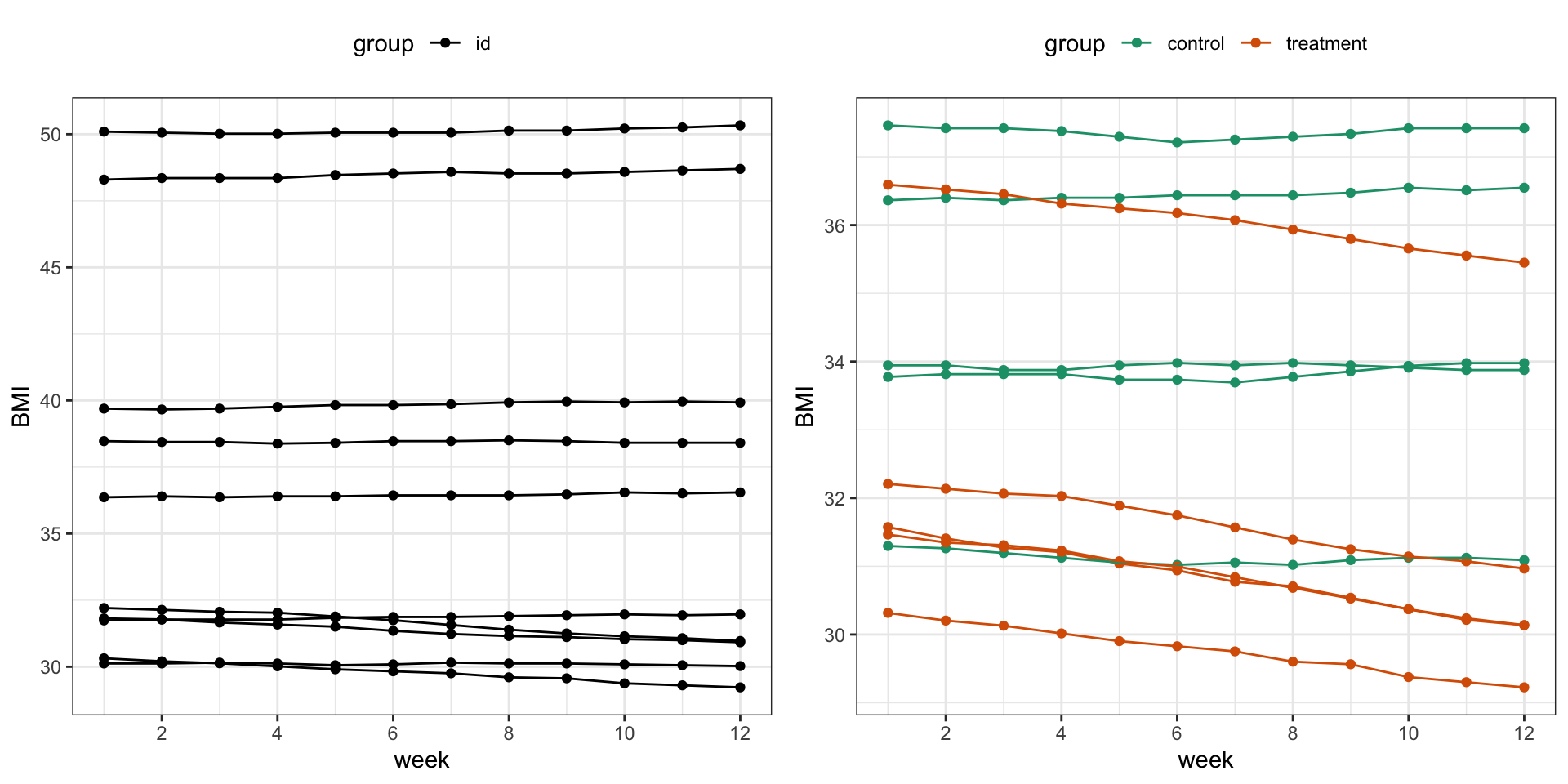
Measures of location & spread

flowchart LR
  A(Representative value) --> C(Image of data)
  B(Spread) --> C(Image of data)

• It is not always easy to get a “feeling” for a set of numerical measurements unless we summarize the data in a meaningful way.
• We can further condense the information shown previously on diagrams by reporting what constitutes a representative value. If we also know how widely scattered the observations are around it, we can formulate an image of data.
• The average is a general term for a measure of location and some common ways of calculating the average are mode, mean and median.

Measures of location

Mode

• Mode values is the value that most common occurs across the measurements. It can be found for numerical and categorical data types.

• For instance, we can find age mode value by counting how many times we observe each age value among the study participants. The top three counts are below and the mode is thus 63.

age	n
63	9
50	6
40	5

• Analogously, we can find mode value for the categorical diabetic status by counting how many of the participants are diabetic and how many are not.

diabetic	n
No	100
Yes	30

Measures of location

Median

Median value divides the ordered data values into two equally sized groups so that 50% of the values are below and 50% are above the median value.

\[\begin{equation} Median = \left\{ \begin{array}{cc} \frac{(n+1)}{2}^{th} term & \mathrm{if\ } n \mathrm{\ is\ odd} \\ \frac{1}{2}\times \left (\frac{n}{2}^{th} term + (\frac{n}{2}+1)^{th} term \right) & \mathrm{if\ } n \mathrm{\ is\ even} \\ \end{array} \right. \end{equation}\]

For instance, the median value for age for the first 10 study participants:

Age values for the first 10 study participants.

1002	1011	1016	1024	1036	1252	1253	1256	1271	1285
58	30	45	60	33	70	47	66	24	40

can be found by ordering observations:

1271	1011	1036	1285	1016	1253	1002	1024	1256	1252
24	30	33	40	45	47	58	60	66	70

and averaging \(5^{th}\) and \(6^{th}\) term in the ordered observations giving a median value of:

[1] 46

Measures of location

Mean & weighted mean

The arithmetic mean, also commonly referred to as mean, is calculated by adding up all the values and diving the sum by the number of values in the data set.

Mathematically, for \(n\) observations \(x_1, x_2, \dots, x_n\), the arithmetic mean value is calculated as: \[\bar x = \frac{x_1+x_2+\dots+x_n}{n} = \frac{1}{n}\displaystyle\sum_{i=1}^n x_i \qquad(1)\]

Weighted mean allows to add weights to certain values of the variable of interest. We attach a weight, \(w_i\) to each of the observed values, \(x_i\), in our sample, to reflect this importance and define the weighted mean as: \[\bar{x} = \frac{w_1x_1 + w_2x_2 + \ldots + w_nx_n}{w_1 + w_2 + \ldots + w_n} = \frac{\displaystyle\sum_{i=1}^{n}w_ix_i}{\displaystyle\sum_{i=1}^{n}w_i} \qquad(2)\]

Measures of location

Mean & weighted mean

Example 1 For instance, we may be interested in knowing an average BMI value, irrespective of gender. It happens that among our study participants women are over represented:

gender	n
male	57
female	73

Assuming BMI measurements for men and women should have equal influence (50/50) and knowing BMI average for men and women separately:

gender	mean_BMI
male	27.77
female	31.71

What is the weighted BMI mean?

Measures of location

Mean, median & outliers

Median is usually preferred when data has outliers as it follows from median definition that is less sensitive to outliers. On the other hand, mean value can be distorted when outliers are present.

Example 2 Let’s add an outlying value of age (110) to the first 11 study participants, and re-calculate mean and median.

	mean	median
without outlier	46.82	45
with outlier	52.08	46

We can see that adding one outlying age value shifted mean age from 46.82 to 52.08 while median age value did not change that much with original median value being 45 and 46 after adding the outlying value.

Measures of location

Mean, median & outliers

In addition, it is good to remember that several very different distributions can still have the same mean value.

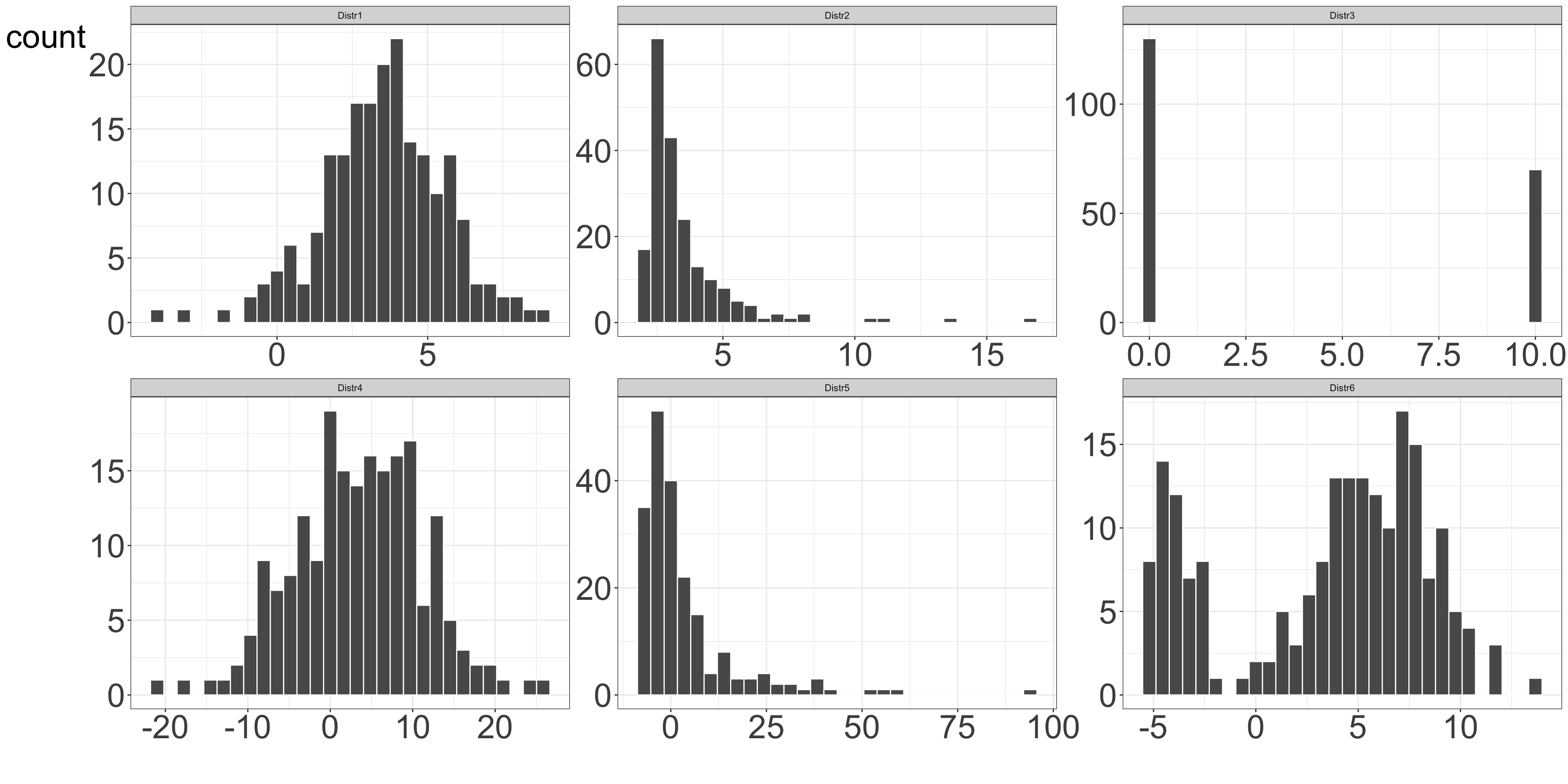
Figure 8: Examples of various distributions having the same mean value of 3.5

Measures of spread

Range, quartiles and IQR

• The range is the difference between the largest and the smallest observations in the data set.
• Quartiles are the three values that divide the data values into four equally sized groups.
• The interquartile range, IQR, is the difference between the 1st (Q1) and the 3rd (Q3) quartiles, i.e. between the 25th and 75th percentiles.

{width = 80%}

Measures of spread

Variance and standard deviation

The variance of a set of observations is their mean squared distance from the mean value:

\[\sigma^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar x)^2 \qquad(3)\]

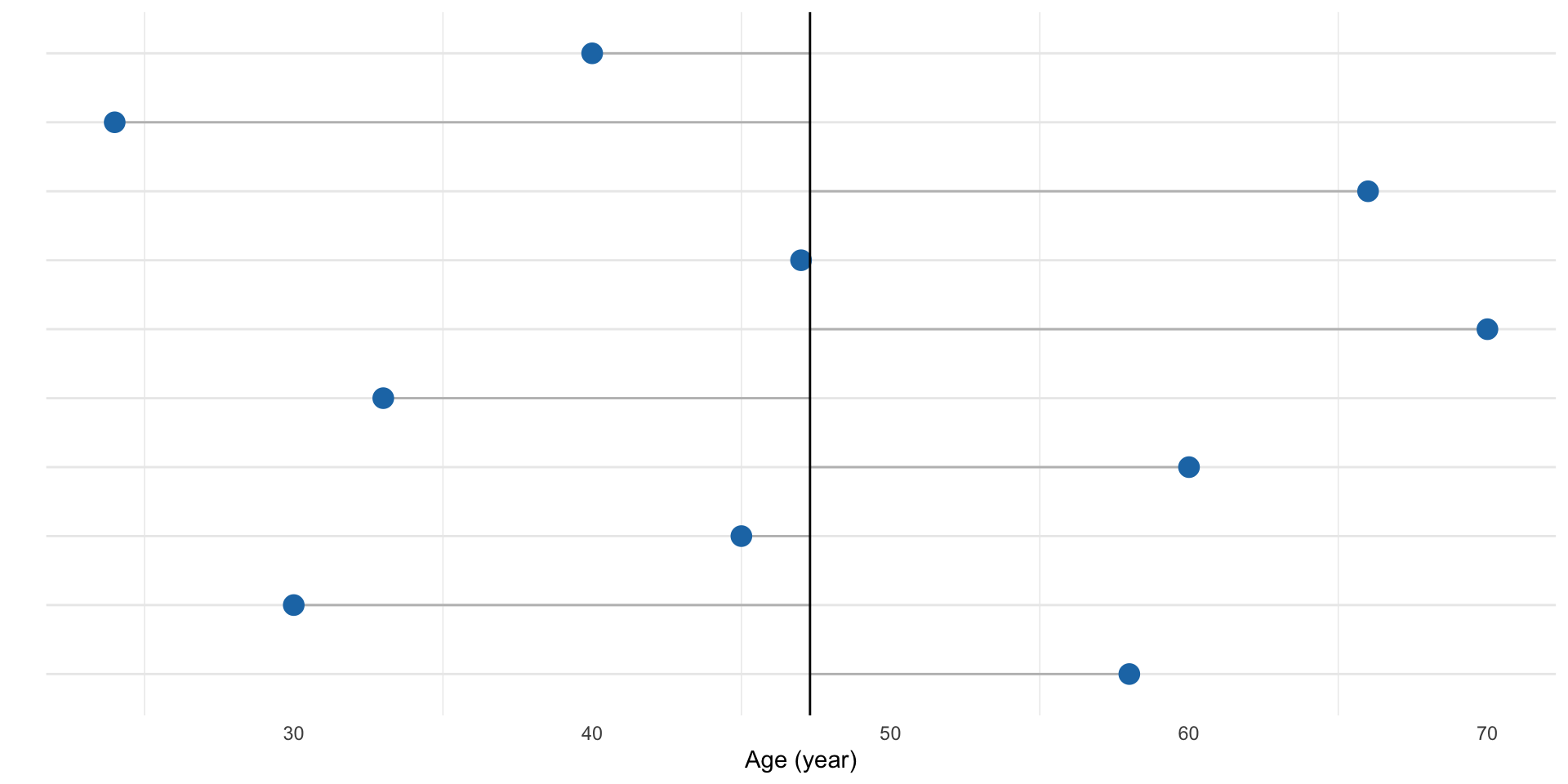
Figure 9: First ten age measurements for the study participants. Grey lines show the distance to the mean age value.

Measures of spread

Variance and standard deviation

Standard deviation is defined as the square root of the variance:

\[\sigma = \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \bar x)^2} \qquad(4)\]

Measures of spread

Sample variance and standard deviation

Typically, we regard the collection of observations \(x_1, \dots, x_n\) as a sample drawn from a large population of possible observations. It has been shown that we obtain a better sample estimate of the population variance and standard deviation if we divide by \((n-1)\). So the denominator \(n\) is commonly replaced by \(n-1\) and the sample variance is calculated instead as:

\[s^2 = {\frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x)^2}. \qquad(5)\]

and the sample standard deviation is calculated as:

\[s = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_i - \bar x)^2}. \qquad(6)\]

A box-and-whisker plot

Boxplot

• A box-and-whisker plot is a diagram summarizing numerical data through quartiles.
• It is shown as a vertical or horizontal rectangle box, with the ends of rectangle corresponding to the upper (Q3) and lower (Q1) quartiles of the data values. A line drawn through the rectangle corresponds to the median value (Q2).
• There can be also lines called whiskers extending from the rectangle indicating variability outside the upper and lower quartiles. These can be defined in few ways¹.
• Data beyond the end of the whiskers are called “outlying” points and are plotted individually.

1. Whiskers can indicate i) minimum and maximum values or ii) particular percentiles, e.g. 5th and 95th. On the box plot prepared with R function boxplot() or geom_boxplot() the upper whisker extends by default to the largest value no further than 1.5 * IQR from Q3 while the lower whiskers extends by default to the smallest value at most 1.5 * IQR from Q1.

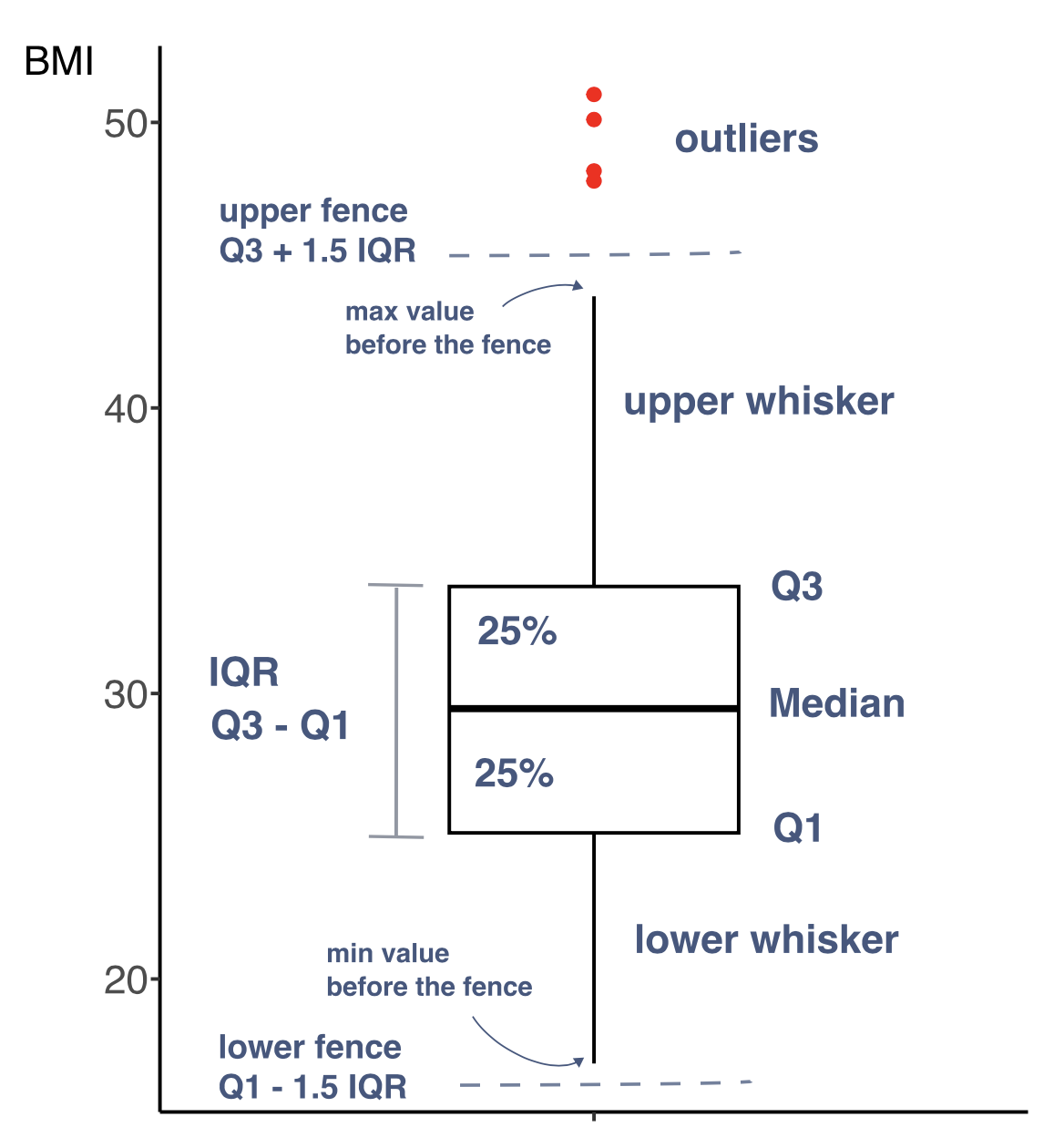
A box-and-whisker plot

Boxplot

• We have recommended to visually assess all the observations.
• We can overlay jitter plot on the box plot to get a complete picture of both the data and the quartiles summary statistics.
• On the right we see a box-and-whisker plot overlayed on the jitter plot for the BMI values based on the measurements for the 130 study participants

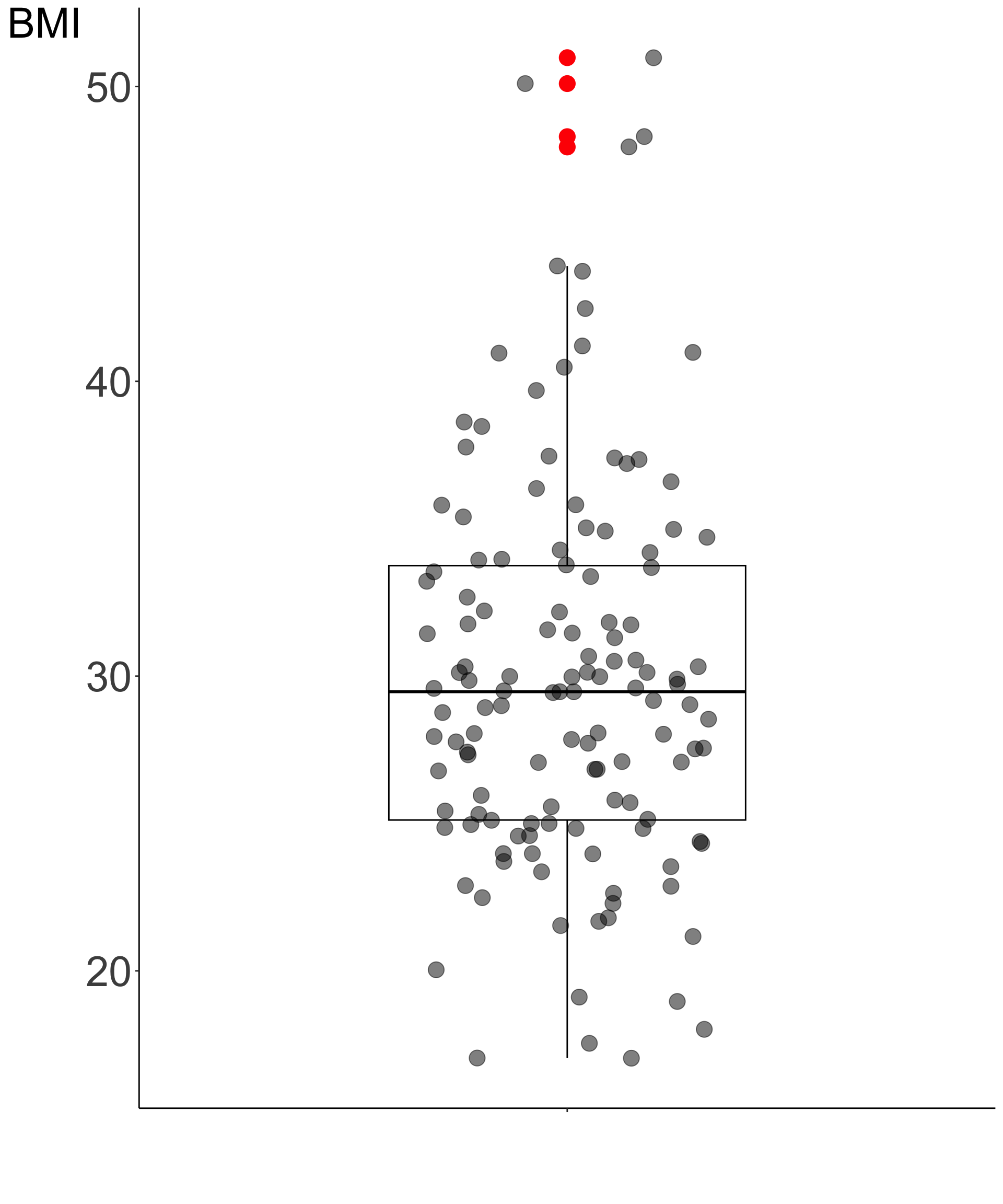
Have you seen these? In which context?

• geometric mean
• trimmed mean
• moving average
• Hodges-Lehmann Estimator
• CV
• MAD
• skewness
• kurtosis

Lifecycle of data science

Descriptive stats in context

flowchart LR
  A(Define problem) --> B(Collect data)
  B --> C(Clean data)
  C --> D(Explore data)
  D --> E(Inferential statistics)
  D --> F(Predictive modelling)
  E --> G(Communicate results)
  F --> G(Communicate results)
  

• Descriptive statistics can be useful in most if not all phases of the project.
• We rely the most on descriptive statistics during the exploring data phase. This phase, is often called Exploratory Data Analysis and abbreviated as EDA.
• EDA was introduced in 1970s by John Tukey to encourage statisticians to explore the data, and formulate hypotheses that could lead to new data collection and experiments.
• Prior the introduction of EDA, initial data analysis, IDA was used with a narrow focus on checking data quality and model assumptions required for statistical modeling and hypothesis testing.

Lifecycle of data science

Descriptive stats in context

flowchart LR
  A(Define problem) --> B(Collect data)
  B --> C(Clean data)
  C --> D(Explore data)
  D --> E(Inferential statistics)
  D --> F(Predictive modelling)
  E --> G(Communicate results)
  F --> G(Communicate results)
  G --> A
  G --> B
  G --> C
  G --> D
  G --> E
  G --> F
  E --> A
  E --> B
  E --> C
  E --> D
  E --> F
  F --> B
  F --> C
  F --> D
  D --> G
  D --> C
  D --> A
  C --> A
  
  

Feature engineering

Feature engineering

And descriptive statistics

flowchart LR
  A(Data) --> B(Descriptive stats.) 
  B --> C(Feature eng.)
  C --> D(ML model)
  C --> B
  

• Feature engineering refers to techniques in machine learning that are used to prepare data for modeling and in turn improve the performance of machine learning models.
• Feature engineering methods go often hand in hand with descriptive statistics.

Feature engineering

scaling & normalization

• Scaling of numerical features
  • Changing the range (scale) of the data to prevent features with larger scales dominating the model.
• Normalization
  • Changing observations so that they can be described by a normal distribution.
  • e.g. going from positive skew: mode < median < mean
  • or going from negative skew: mode > median > mean

Feature engineering

common transformations

square-root for moderate skew

• sqrt(x) for positively skewed data,
• sqrt(max(x+1) - x) for negatively skewed data

log for greater skew

• log10(x) for positively skewed data,
• log10(max(x+1) - x) for negatively skewed data

inverse for severe skew

• 1/x for positively skewed data
• 1/(max(x+1) - x) for negatively skewed data

Feature engineering

dummy variables

• Representing categorical variables with dummy variables or one-hot encoding to create numerical features.
  • For instance a categorical variable obese with three possible vales (underweight, healthy, overweight) can be transformed into two binary variables: “is_healthy”, and “is_overweight”, where the value of each variable is 1 if the observation belongs to that category and 0 otherwise. Only \(k-1\) binary variables to encode \(k\) categories.
• In one-hot encoding \(k\) binary variables are created.

Example of obese variable with three categories (underweight/healthy/overweight) encoded as dummy variables

id	obese	is_healthy	is_overweight
902	Overweight	0	1
911	Healthy	1	0
916	Healthy	1	0
1171	Underweight	0	0
1185	Healthy	1	0

Feature engineering

missing data

• handling missing data via
  • imputations (mean, median, KNN-based)
  • deleting strategies such as list-wise deletion (complete-case analysis) or pair-wise deletion (available-case analysis)
  • choosing algorithms that can handle some extent of missing data, e.g. Random Forest, Naive Bayes

Feature engineering

Rubin’s (1976) missing data classification system

MCAR

• missing completely at random

MAR

• missing at random
• two observations for Test 2 deleted where Test 1 \(<17\)
• missing data on a variable is related to some other measured variable in the model, but not to the value of the variable with missing values itself

MNAR

• missing not at random
• omitting two highest values for Test 2
• when the missing values on a variable are related to the values of that variable itself

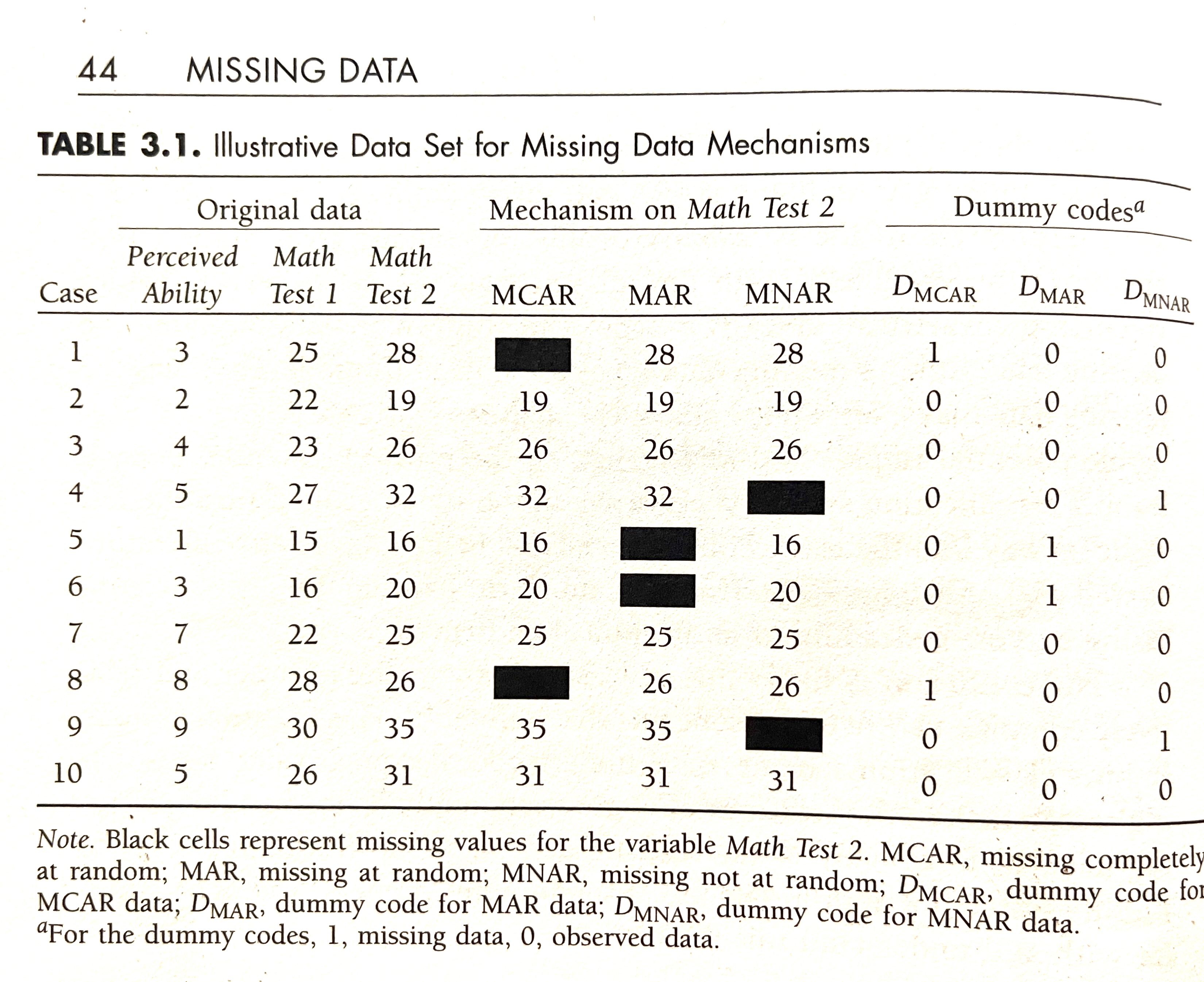“Missing Data: A Gentle Introduction by Patrick E. McKnight, Katherine M. McKnight, Souraya Sidani, and Aurelio Jose Figueredo” (2008)

Feature engineering

handling imbalanced data

• handling imbalanced data
  • down-sampling
  • up-sampling
  • generating synthetic instances
    • e.g. with SMOTE (Fernández et al. 2018)
    • or ADASYN (He et al. 2008)

Feature engineering

misc

• feature aggregation
  • e.g. combining multiple related features into a single one, e.g. calculating average of a group
• feature interaction: creating new features by combining existing features
  • e.g. creating BMI variables based on weight and height
• dimensionality reduction: reducing number of features in a data set by transforming them into a lower-dimensional space
• filtering out irrelevant features
  • e.g. using variance threshold or univariate statistics
• filtering out redundant features
  • e.g. keeping only one of a group of highly correlated features
  • Note: collinearity reduces the accuracy of the estimates of the regression coefficients and thus the power of the hypothesis testing is reduced.

Summary

• Descriptive statistics is usually the first step of data analysis in which we try to familiarize ourselves with the data
• Numerical summaries displaying data diagrammatically give us idea about data distributions. They can also uncover some errors or outliers as well as emerging patterns in the data.
• Often, descriptive statistics together with data cleaning and processing, is the most time-consuming part of a bioinformatics project.

It is always a good idea to look at the raw measurements, printing them all for smaller data sets or printing randomly selected measurements from bigger data sets.

In practice

• There are many R packages to calculates descriptive statistics and presents the results in customizable summary table ready for publication, e.g. gtsummary or arsenal.

• Similarly, there are many ways of visualizing the data. For inspiration The R Graph Gallery https://r-graph-gallery.com

• We will later learn how to use tidymodels framework to run ML models tasks, including feature engineering steps with recipes tidy interface.

Table 2:

Example of the gtsummary table.

Characteristic	No, N = 2531	Yes, N = 1441
age	47 (17)	47 (16)
chol	206 (43)	212 (46)
Unknown	1	0
gender
male	128 (51%)	40 (28%)
female	125 (49%)	104 (72%)
1 Mean (SD); n (%)

Thank you

questions?

References

Fernández, Alberto, Salvador Garcia, Francisco Herrera, and Nitesh V Chawla. 2018. “SMOTE for Learning from Imbalanced Data: Progress and Challenges, Marking the 15-Year Anniversary.” Journal of Artificial Intelligence Research 61: 863–905.

He, Haibo, Yang Bai, Edwardo A. Garcia, and Shutao Li. 2008. “ADASYN: Adaptive Synthetic Sampling Approach for Imbalanced Learning.” In 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), 1322–28. https://doi.org/10.1109/IJCNN.2008.4633969.

“Missing Data: A Gentle Introduction by Patrick E. McKnight, Katherine M. McKnight, Souraya Sidani, and Aurelio Jose Figueredo.” 2008. Personnel Psychology 61 (1): 218–21. https://doi.org/10.1111/j.1744-6570.2008.00111_8.x.