2.1 Prevalence

We aggregate the number of tests in each village. We look at the dimension of the unique coordinates and see that the 2035 tests are conducted in 65 unique locations.

dim(gambia)
dim(unique(gambia[, c("x", "y")]))

## [1] 2035    8
## [1] 65  2

We create a data frame called d containing the village coordinates (x, y), the total number of tests performed (total), the number of positive tests (positive), and the malaria prevalence (prev) in each village. Positive tests results have pos equal to 1 and negative test results have pos equal to 0. Therefore, we can calculate the number of positive tests in each village adding up the elements in gambia$pos. We calculate the prevalence in each village by calculating the proportion of positive tests (number of positive results divided by the total number of tests in each village).

library(dplyr)
d <- group_by(gambia, x, y) %>% 
  summarize(total = n(),
            positive = sum(pos),
            prev = positive/total)
head(d)

2.2 Transform coordinates

Now, we can plot the malaria prevalence in a leaflet map. leaflet expects data to be specified in geographic coordinates (latitude/longitude). However, the coordinates in the data are in UTM format (Easting/Northing). We transform the UTM coordinates in the data to geographic coordinates using the spTransform() function of the sp package.

First, we create a SpatialPoints object called sps using the sp package where we specify the projection of The Gambia, that is, UTM zone 28. Then, we transform the UTM coordinates in sps to geographic coordinates using spTransform() where we set CRS to CRS("+proj=longlat +datum=WGS84").

library(sp)
library(rgdal)
sps  <- SpatialPoints(d[, c("x", "y")], proj4string = CRS("+proj=utm +zone=28"))
spst <- spTransform(sps, CRS("+proj=longlat +datum=WGS84"))

Finally, we add the longitude and latitude variables to the data frame d.

d[, c("long", "lat")] <- coordinates(spst)
head(d)

2.3 Map prevalence

Now we use leaflet() to construct a map with the locations of the villages and the malaria prevalence. We use addCircles() to put circles on the map, and colour circles according to the value of the prevalences. We choose a palette function with colours from viridis and four equal intervals from values 0 to 1. We use the base map given by providers$CartoDB.Positron so point colours can be distinguised from the background map. We also add a scale bar using addScaleBar().

library(leaflet)
pal <- colorBin("viridis", bins = c(0, 0.25, 0.5, 0.75, 1))
leaflet(d) %>%  addProviderTiles(providers$CartoDB.Positron) %>%
  addCircles(lng = ~long, lat = ~lat, color = ~pal(prev)) %>%
   addLegend("bottomright", pal = pal, values = ~prev, title = "Prevalence") %>%
  addScaleBar(position = c("bottomleft"))

2.4 Environmental covariates

To model malaria prevalence we will use a covariate that indicates the elevation in The Gambia. This covariate can be obtained with the getData() function of the raster package which can be used to obtain geographic data from anywhere in the world. In order to get the elevation values in The Gambia, we need to call getData() with the three following arguments:

• name of the data set to 'alt',
• country set to the 3 letters of the International Organization for Standardization (ISO) code of The Gambia (GMB), and
• mask set to TRUE so the neighbouring countries are set to NA.

library(raster)
r <- getData(name = 'alt', country = 'GMB', mask = TRUE)

We make a map with the elevation raster using the addRasterImage() function of the leaflet package. First we create a palette function pal using the values of the raster (values(r)) and specifying that the NA values are transparent.

pal <- colorNumeric("viridis", values(r), na.color = "transparent")

leaflet() %>% addProviderTiles(providers$CartoDB.Positron) %>%
  addRasterImage(r, colors = pal, opacity = 0.5) %>%
  addLegend("bottomright", pal = pal, values = values(r), title = "Altitude") %>%
  addScaleBar(position = c("bottomleft"))

We also add the elevation variable to the data frame d because we will use it as a covariate in the model. To do that we get the altitude values at the villages locations using the extract() function of the raster package. The first argument of this function is the elevation raster (r). The second argument is a two column matrix with the coordinates where we want to know the values, that is, the coordinates of the villages given by d[ ,c("long", "lat")]. We assign the altitude vector to the column alt of the data frame d.

d$alt <- extract(r, d[, c("long", "lat")])

2.5 Data

The final dataset is this:

head(d)

3.1 Model

Conditional on the true prevalence \(P(x_i)\) at location \(x_i\), \(i = 1, \ldots, n\), the number of positive results \(Y_i\) out of \(N_i\) people sampled at \(x_i\) follows a binomial distribution,

\[Y_i|P(x_i) \sim Binomial(N_i, P(x_i)),\]

\[logit(P(x_i)) = \beta_0 + \beta_1 \times \mbox{altitude} + S(x_i)\] Here \(\beta_0\) denotes the intercept, \(\beta_1\) is the coefficient of altitude, and \(S(x_i)\) is a spatially structured random effect which follows a zero-mean Gaussian process with Matern covariance function: \[\mbox{Cov}(S(x_i),S(x_j))=\frac{\sigma^2}{2^{\nu-1}\Gamma(\nu)}(\kappa ||x_i - x_j ||)^\nu K_\nu(\kappa ||x_i - x_j ||).\] Here, \(K_\nu\) is the modified Bessel function of second kind and order \(\nu>0\). \(\nu\) is the smoothness parameter, \(\sigma^2\) denotes the variance, and \(\kappa >0\) is related to the practical range \(\rho = \sqrt{8 \nu}/\kappa\), the distance at which the spatial correlation is close to 0.1.

3.2 Build mesh

Then, we need to build a triangulation mesh that covers The Gambia over which to make the random field discretization. For building the mesh, we use the inla.mesh.2d() function passing the following parameters:

• loc: locations coordinates that will be used as initial mesh vertices,
• max.edge: values denoting the maximum allowed triangle edge lengths in the region and in the extension,
• cutoff: minimum allowed distance between points.

Here, we call inla.mesh.2d() setting loc equal to the matrix with the coordinates coo. We set max.edge = c(0.1, 5) to use small triangles within the region, and larger triangles in the extension. cutoff = 0.01 to avoid building many small triangles where we have some very close points.

library(INLA)
coo <- cbind(d$long, d$lat)
mesh <- inla.mesh.2d(loc = coo, max.edge = c(0.1, 5), cutoff = 0.01)

The number of vertices is given by mesh$n and we can plot the mesh with plot(mesh).

mesh$n
plot(mesh)
points(coo, col = "red")

## [1] 686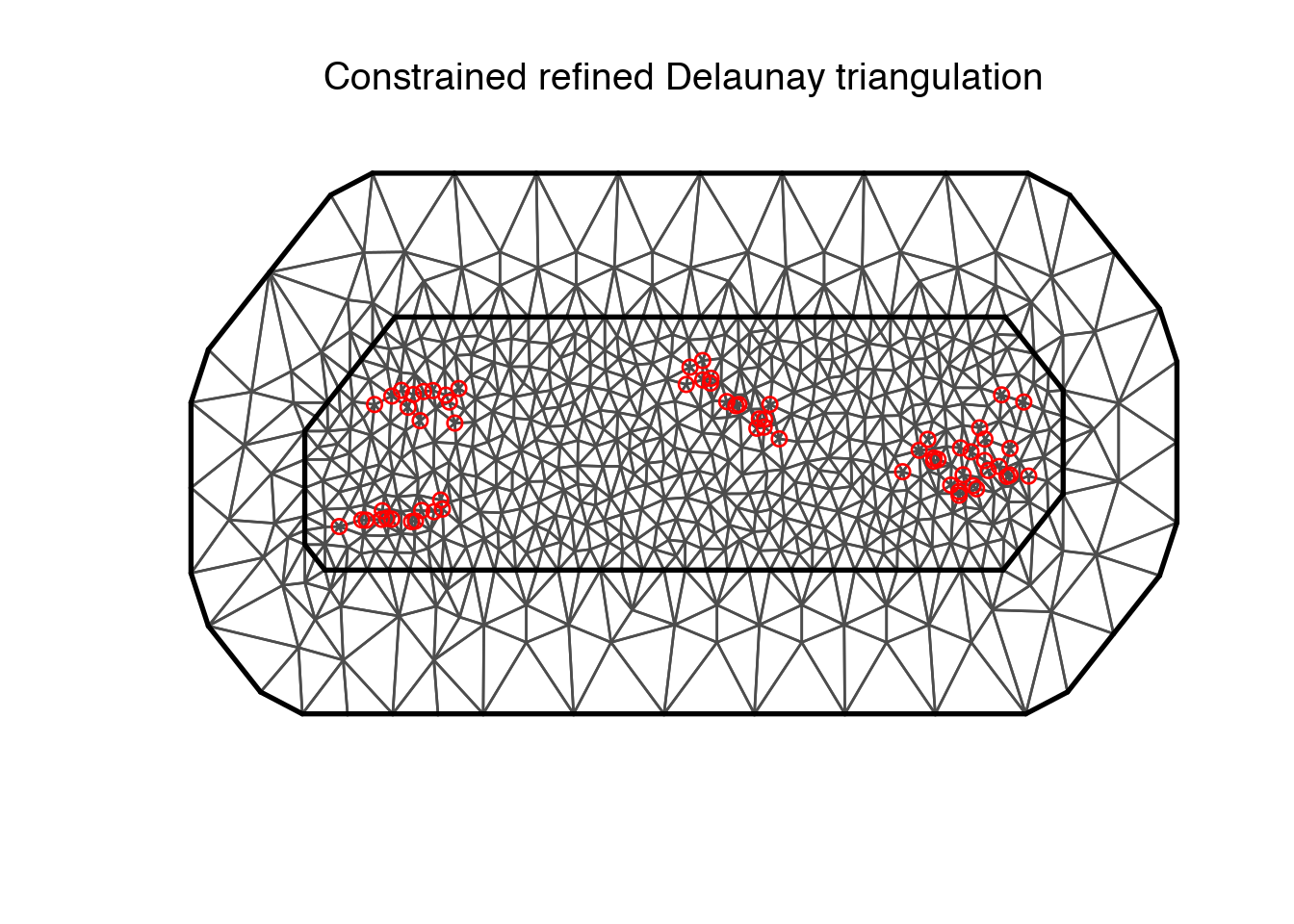

3.3 Build the SPDE model on the mesh

Then, we use the inla.spde2.matern() function to build the SPDE model.

spde <- inla.spde2.matern(mesh = mesh, alpha = 2)

Here alpha is a parameter related to the smoothness parameter of the process: \(\alpha=\nu+d/2\). Here, we set the smoothness parameter \(\nu\) equal to 1, and in the spatial case \(d=2\). Therefore alpha=1+2/2=2.

3.4 Index set

Now we generate the index set for the SPDE model. We do this with the function inla.spde.make.index() where we specify the name of the effect (s) and the number of vertices in the SPDE model (spde$n.spde). This creates a list with vector s equal to 1:spde$n.spde, and vectors s.group and s.repl that have all elements equal to 1s and size given by the number of mesh vertices.

indexs <- inla.spde.make.index("s", spde$n.spde)
lengths(indexs)

##       s s.group  s.repl 
##     686     686     686

3.5 Projector matrix

We need to build a projector matrix A that projects the spatially continuous Gaussian random field at the mesh nodes. The projector matrix A can be built with the inla.spde.make.A() function passing the mesh and the coordinates.

A <- inla.spde.make.A(mesh = mesh, loc = coo)

3.6 Prediction data

Here we specify the locations where we want to predict the prevalence. We set the prediction locations to the locations of the the covariate raster data. We can get the coordinates of the raster r with the function rasterToPoints() of the raster package. This function returns a matrix with the coordinates and values of the raster that do not have NA values. We see there are 12964 points.

dp <- rasterToPoints(r)
dim(dp)

## [1] 12964     3

In this example, we want to use fewer prediction points. We can lower the resolution of the raster by using aggregate() of the raster package. The arguments of the function are

• x: the raster object,
• fact: aggregation factor expressed as number of cells in each direction (horizontally and vertically),
• fun: function used to aggregate values.

We specify fact = 5 aggregating 5 cells in each direction, and fun = mean to compute the mean of the cell values. We call coop to the matrix of coordinates with the prediction locations.

ra <- aggregate(r, fact = 5, fun = mean)

dp <- rasterToPoints(ra)
dim(dp)
coop <- dp[, c("x", "y")]

## [1] 627   3

3.7 Projector matrix

We also construct the matrix that projects the locations where we will do the predictions.

Ap <- inla.spde.make.A(mesh = mesh, loc = coop)

3.8 Stack data for the estimation and prediction

Now we use the inla.stack() function to organize data, effects, and projector matrices. We use the following arguments:

• tag: string for identifying the data,
• data: list of data vectors,
• A: list of projector matrices,
• effects: list with fixed and random effects.

We construct a stack called stk.e with data for estimation and we tag it with the string "est". The fixed effects are the intercept (b0) and a covariate (cov). The random effects is the spatial Gaussian Random Field (s). Therefore, in effects we pass a list with a data.frame with the fixed effects, and a list s containing the indices of the SPDE object (indexs). A is set to a list where the second element is A, the projector matrix for the random effects, and the first element is 1 to indicate the fixed effects are mapped one-to-one to the response. In data we specify the response vector and the number of trials. We also construct a stack for prediction that called stk.p. This stack has tag "pred", the response vector is set to NA, and the data is specified at the prediction locations. Finally, we put stk.e and stk.p together in a full stack stk.full.

#stack for estimation stk.e
stk.e <- inla.stack(tag = "est",
data = list(y = d$positive, numtrials = d$total),
A = list(1, A),
effects = list(data.frame(b0 = 1, cov = d$alt), s = indexs))

#stack for prediction stk.p
stk.p <- inla.stack(tag = "pred",
data = list(y = NA, numtrials = NA),
A = list(1, Ap),
effects = list(data.frame(b0 = 1, cov = dp[, 3]), s = indexs))

#stk.full has stk.e and stk.p
stk.full <- inla.stack(stk.e, stk.p)

3.9 Model formula

We specify the model formula by including the response in the left-hand side, and the fixed and random effects in the right-hand side. In the formula we remove the intercept (adding 0) and add it as a covariate term (adding b0), so all the covariate terms can be captured in the projector matrix.

formula <- y ~ 0 + b0 + cov + f(s, model = spde)

3.10 Call inla()

We fit the model by calling inla() and using the default priors in INLA. We specify the formula, family, data, and options. In control.predictor we set compute = TRUE to compute the posterior means of the predictors. We set link=1 to compute the fitted values (res$summary.fitted.values and res$marginals.fitted.values) with the same link function as the the family specified in the model.

res <- inla(formula, family = "binomial", Ntrials = numtrials,
control.family = list(link = "logit"),
data = inla.stack.data(stk.full),
control.predictor = list(compute = TRUE, link = 1, A = inla.stack.A(stk.full)))

3.11 Results

We inspect the results by typing summary(res).

summary(res)

## 
## Call:
## c("inla(formula = formula, family = \"binomial\", data = inla.stack.data(stk.full), ",  "    Ntrials = numtrials, control.predictor = list(compute = TRUE, ",  "        link = 1, A = inla.stack.A(stk.full)), control.family = list(link = \"logit\"))" )
## 
## Time used:
##  Pre-processing    Running inla Post-processing           Total 
##          2.0369         21.5313          0.3500         23.9182 
## 
## Fixed effects:
##        mean     sd 0.025quant 0.5quant 0.975quant    mode kld
## b0  -0.1893 0.5271    -1.0806  -0.2377     1.0082 -0.3019   0
## cov -0.0117 0.0107    -0.0325  -0.0118     0.0098 -0.0120   0
## 
## Random effects:
## Name   Model
##  s   SPDE2 model 
## 
## Model hyperparameters:
##                mean    sd 0.025quant 0.5quant 0.975quant   mode
## Theta1 for s -4.021 0.296     -4.598   -4.024     -3.435 -4.031
## Theta2 for s  2.665 0.377      1.915    2.669      3.400  2.681
## 
## Expected number of effective parameters(std dev): 43.17(3.967)
## Number of equivalent replicates : 1.506 
## 
## Marginal log-Likelihood:  -216.29 
## Posterior marginals for linear predictor and fitted values computed